基于FNN的机器人局部路径规划中实际隶属函数的推导*
2012-12-03熊开封
熊开封 张 华
(西南科技大学国家级综合性工程训练中心 四川绵阳 621010)
在移动机器人的控制中,路径规划是其中关键问题之一。移动机器人路径规划就是移动机器人在具有障碍物的环境中按照一定的评价标准(如工作代价最小、行走路径最短、行走时间最短等),寻找一条从给定起点到达目标终点的无碰路径[1]。避碰与寻最优路径是机器人路径规划中的两个重点。而在动态环境下,障碍物既有静态亦有动态,因而采用在线的局部路径规划。常用的机器人路径规划方法有基于势场法和可视顶点图法等,但这些方法都有其一定的缺点,因此不适用于在动态环境中进行局部路径规划[2]。而模糊神经网络(FNN)由于综合了模糊理论和神经网络理论两者的优点,已为许多学者证明是全局逼近器[3-4],因而成为机器人局部路径规划的一个研究热点。而应用FNN的一个重点就是选择合理的隶属函数,确保机器人安全避碰,至于函数的参数可以由神经网络超强的自学习能力“学习”得到。本文结合动态环境下机器人路径规划的实际,着重对文献[1]和文献[5]提出的两种具有实际意义的隶属函数进行比较研究,并在其基础上提出一种新的隶属函数。
1 具有实际意义的隶属函数
常规的隶属函数相对被控模型来说,一般没有明确的物理意义。动态环境下机器人路径规划中建立符合客观实际的隶属函数,主要是解决避碰问题,即利用机器人和各个障碍物的实时运动信息,如某时刻的速度、位置、行进方向,提出一种具有明确物理意义的函数作为模糊隶属函数,来表达机器人和各移动障碍物之间运动情况的可能性[5]。
在文献[2]中定义其隶属函数为:
(1)
上式表示的物理意义是:如果机器人和障碍物之间的距离很小且相互间的相对运动速度很大,则发生碰撞的可能性很大;若两者间的距离较大而相互运动速度较小,则发生碰撞的可能性较小;如果两者间的距离很大,则发生碰撞的可能性可以忽略[1]。其中,(x,y)和(xi,yi)、v和vi分别为移动机器人及第i个障碍物某时刻的位置、速度,α和αi分别为移动机器人和移动障碍物运动方向与这两点连线的夹角;Ri对于每个障碍物是不同的,它表示隶属函数的宽度。
在文献[5]中定义其隶属函数为:
(2)
该式表达的物理意义是:当机器人和移动障碍物之间的距离大于在单位时间内机器人和移动障碍物靠近的距离时,机器人与移动障碍物之问发生碰撞的可能性为0;当机器人和移动障碍物之间的距离小于单位时间内机器人和移动障碍物靠近的距离时,机器人和移动障碍物之间有可能发生碰撞,分子越小于分母,则发生碰撞的可能性越大[5]。其中,(xn,yn)和(xion,yion)、vn和vion、Ri的含义类似于(1)式,而φrn,φion分别为移动机器人及第i个障碍物某时刻的速度相对于坐标系横轴的夹角。
2实例分析

由(2)式可知,
φrn=φion=0,cosφrn=cosφion=1,sinφrn=sinφion=0,
会出现D>Di,认为R与O将不会发生碰撞或发生碰撞的可能性很小,与实际矛盾。而(1)式的判断是吻合实际的。

图1 机器人R与障碍物O同向同域运动函数构建

图2 机器人R与障碍物O距离与碰撞可能性函数构建
推论1:当α=0且D逐步缩小时,即R与O同线相向移动,R与O实际发生碰撞的可能性很大。而(1)(2)式均会得出与实际矛盾的结论。(1)式中:αi=π,Di=Ri(vcosα+vicosαi)=Ri(vcos0+vicosπ)=Ri(v-vi) (2)式的分析类似于例1。 推论2:当αi=π且D逐步增大时,即R与O同线背向移动,R与O实际发生碰撞的可能性为0。而(1)(2)式均会得出与实际矛盾的结论。 由实例分析可见,式(1)主要考虑了机器人与障碍物的距离和两者的相对运动速度的大小,而缺少没有加入和,式(2)在考虑了机器人与障碍物的距离的基础上引入了两者单位时间内相对移动距离的大小,都忽略了对运动方向的重视。因此,在文献[2]和文献[5]的基础上,笔者提出如下改进的具有实际意义的隶属函数。 (3) 其中,(x,y)和(xi,yi)、v和vi分别为移动机器人及第i个障碍物某时刻的位置、速度,φrn,φion分别为移动机器人及第i个障碍物某时刻的速度方向相对于坐标系横轴的夹角,θ为移动机器人的运动速度方向与机器人和障碍物两点连线的夹角;Ri对于每个障碍物是不同的,它表示隶属函数的宽度;ε为任意小的小数或0,可以根据实际设定。 其物理意义是,当机器人和移动障碍物之间的距离大于在单位时间内机器人和移动障碍物靠近的距离时,机器人与移动障碍物之问发生碰撞的可能性为0;当机器人和移动障碍物之间的距离小于单位时间内机器人和移动障碍物靠近的距离时,机器人和移动障碍物之间有可能发生碰撞;在机器人运动方向越背离障碍物时,发生碰撞的可能性就越小[6]。 模糊神经网络是动态环境下机器人路径规划中应用的一种重要智能方法,常规隶属函数选用的主要是高斯函数、三角函数,但实际意义不太明确。笔者在前人工作的基础上,综合考虑二维直角坐标体系下机器人、障碍物的位置、速度及运动方向,理论推导出一种新的具有实际含义的隶属函数,至于该函数的合理性与优越性,还有待于后期程序编译等方式来验证。 参考文献: [1]付永前.移动机器人运动控制与路径规划研究[D].武汉:华中科技大学,2005. [2]谢宏斌,刘国栋,李春光.动态环境中基于模糊神经网络的机器人路径规划的一种新方法[J].江南大学院学报(自然科学版),2003,2(1):20. [3]Wang L X,Mendal J M. Fuzzzy basic functions,universal approximation,and orthogonal least squares learning[J].IEEE Trans on Neural Networks,1992,3(5):807. [4]王立新.自适应模糊系统与控制[M].北京:国防工业出版社,1995.105. [5]张寒松,贾瑞清.基于实际函数的机器人模糊神经网络路径规划[J].矿山机械,2010.38(14):45. [6]张寒松,贾瑞清,王廷军,等.基于实际意义误差函数的机器人避碰模糊神经网络算法[J].矿山机械,2006,34(2):16.3 一种改进的隶属函数
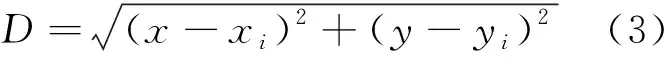
4结束语
