分期BOT项目期权定价特许权期的决策模型与分析

张俊生，王广斌

（同济大学 经济与管理学院，上海200092）

城市基础设施（譬如高速公路、机场、港口和环保设施等）随着经济建设和现代化进程的不断深入，逐渐成为调整城市结构、支撑城市深入发展的必要的硬件设施.然而，这些基础设施通常投资金额巨大，建设期限较长，政府往往没有足够的财政资金进行这些城市基础设施的建设.BOT 融资方式，即建设（Build）经营（Operate）移交（Transfer），成为利用民营资本进行基础设施建设的一种有效的项目融资方式，特别是交通和环保基础设施.譬如，2008年建成通车的杭州湾跨海大桥（总投资达118亿元），就是一个民营资本首度进入“国字号”工程并参与投资、建设和经营的实例.

BOT 融资方式的具体做法是，成立专门的项目公司与政府签署特许权合同，或者基础设施项目投资、建设和经营的“特许权”，在特许权期内，项目公司通过对项目经营取得收入，以弥补投融资成本、运营和维护成本，同时获得一定利润，当特许权期结束时，项目公司按约定将该设施完整、无偿地移交给政府部门，转由政府部门来进行经营管理［1－2］.它不但已广泛应用于城市基础设施建设当中，而且在学术研究领域也受到众多学者广泛关注，并对相关问题进行了深入的研究.

李启明等［3］通过分析确定特许权期的若干原则和作用及其影响因素，建立了从收益和现金流量的角度描述基础设施BOT 特许权期的决策模型.进一步，杨屹等［4］一些学者利用期权博弈理论对分期投资决策进行了研究和探索.研究表明，政府可以把基础设施BOT 项目分成若干阶段分别进行投资建设，并且赋予项目公司可以投资项目下一阶段的权利，这一投资权利就是一种实物期权，即增长期权.

文献［1］中把实物期权方法和博弈论结合起来，建立分期BOT 项目期权博弈模型，分析问题显示了项目不确定性和主体相互作用对BOT 项目价值的重大影响.假设第一期建设时间为m，第二期建设时间为n，特许权期为T，该模型的分期BOT 模式示意图如图1所示.

分期期权博弈模型能够弥补传统项目评价方法的缺陷，既能有效地提升政府在特许权协议谈判中的博弈空间，增强政府在项目建设过程中的监督能力，又能减少项目公司一次性的资金投入，激励项目公司提高BOT 项目的建设质量，从而提高政府和企业的收益，降低风险.

图1 不分期BOT模式与分期BOT模式的示意图Fig.1 Diagram of BOT model and BOT model by stages

众所周知，合理科学地分担BOT 项目的建设质量风险和投资回报风险是政府和项目公司双方角逐的重点，也是学者研究的热点问题之一，而解决这些问题的关键是如何科学地确定BOT 项目的特许权期.从该模型可以看出，分期期权博弈模型中第一期和第二期项目移交年份不一样，而实际经营过程中，政府和项目公司往往希望该项目能够灵活选择合适的特许权期，譬如第一期和第二期完成后整体移交，这就需要缩短二期项目的特许权期，而延长一期项目的特许权期.因此，对于分期BOT 项目，如何合理确定这一特许权期是本文讨论的主要内容.

1 分期期权博弈模型

BOT 项目传统的投资决策方法局限于折现现金流（DFC）一类的财务方法，譬如：净现值法（NPV）、内部收益率法（IRR）和投资回收期等.其中，净现值法是最经典和应用最广泛的方法.但是，这类投资决策方法在基本假设方面存在明显的缺陷和不足，在应用过程中也有无法克服的障碍.

针对折现现金流法所存在的这些缺陷，经济学家提出了一种比较独特和科学的实物期权法.由于折现现金流法最大的缺点在于不能为管理灵活性和不确定性定价，而实物期权恰好能够反映决策灵活性和不确定性的价值，因而被迅速地引入到投资项目的决策分析中来.由于城市基础设施投资BOT 项目具有很大的不确定性，导致该项目具有期权性质，因此用实物期权评价方法比传统的净现值法等更具有吸引力.

1.1 实物期权模型

期权就是在投资者付出一定代价后获得在一定时间或在某时间之前的任一时刻按规定的价格买入或卖出一定数量某种资产的一种权利.期权是一种“或有决策”的权利，而不是义务，它允许期权所有者根据市场条件的变化而采取不同的行动.在决策时刻，假如情况比预期要好或估计会向好的方向发展，就应该执行期权，否则就放弃期权.即使放弃行使期权，投资者所受到的损失相对于一开始就做出投资决策而言也是非常小的.可见，作为规避风险并可从中获利的一种金融工具，期权特别适合不确定性因素较多的市场环境.期权为人们应对市场风险提供了能动性和灵活性.

在期权定价的研究中，最著名的是Black－Scholes期权定价模型，该模型假设：①市场为完全市场，市场中不存在交易成本及信息不对称；②在项目存续期，无风险利率是已知的，并且保持不变；③投资产生的现金流量遵循对数正态分布的随机过程；④看涨期权只能在到期日执行.

假设看涨期权价值为C，其公式为

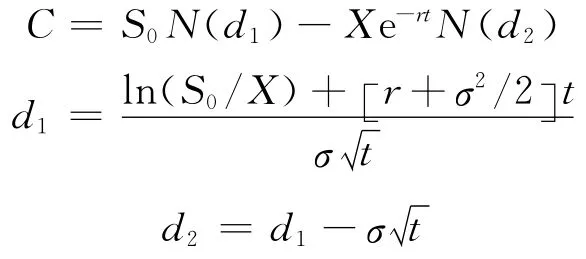
式中：S0表示项目的当前价值即标的资产的现值；N（d）表示标准正态分布中离差小于d的概率；X表示项目期权的执行价格即投资成本；r为无风险收益率；t为投资项目期权到期时间；σ为项目价值的波动率.关于期权的模型和定价，详见文献［5］.

实物期权（real option）是指存在于实物资产投资中，且具有期权性质的权利.它是由美国麻省理工学院的经济学家Stewart Myers提出，是金融期权在实物领域的拓展和应用.实物期权的核心思想理念就是：投资项目的价值不仅来自项目预测的现金流量，还来自于项目的成长机会.与传统的投资决策分析方法相比较，实物期权的思想不是集中于对单一现金流的预测，而是将分析集中在项目所具有的不确定性问题上，用概率的语言来描述项目未来现金流的概率分布状况.实物期权隐含在投资项目中，项目的不确定性越大，期权的价值越大.实物期权的思想很快应用到实际工程的管理中，并引起了国内外学者的广泛关注和研究［1，4，6］.

用实物期权的方法对投资项目进行评价，投资项目的价值可以分成两个部分，一部分是不考虑项目期权价值的价值，这正是传统投资决策方法中的净现值N，另一部分是投资项目的期权价值C.因此，引入实物期权理论以后，投资项目的总价值P可表示为：P＝N＋C.

譬如，某项目需要建设期为k，总投资成本为c，特许经营期为l（不含建设期），每年扣除维护成本收益为p.那么，用净现值法计算该项目的总价值为

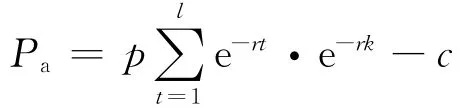
实物期权是动态的战略决策过程，适用于对投资量大、周期长、阶段性强、波动性大的项目进行评价.也就是说，项目价值不只是由当前现金流决定的，而主要是由未来变化决定的.不确定性足够大的项目、存在或有投资决策的项目以及需要战略修正的项目一般都可以采用实物期权法进行评价.

1.2 分期实物期权模型

由于基础设施投资BOT 项目投资规模巨大，建设周期较长，具有很大的不确定性，因此一次性投资对政府和项目公司来说都有很大的风险.BOT 项目分期实施能提升政府在谈判中的博弈空间，又能减少项目公司的一次性的资金投入，是一项双赢的决策模型.通过期权博弈模型能够激励项目公司提高BOT 项目的建设质量，从而提高政府和企业的收益，降低风险.

假设转交政府运营的时间和上面不分期BOT项目一样，该BOT 项目分期实施，第一期建设时间为m，投资成本为c1，每年扣除维护成本收益为p1，第二期建设时间为n，投资成本为c2，每年扣除维护成本收益为p2.假设有

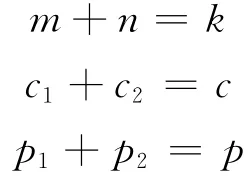
第一期项目可用净现值法计算该项目的价值，第二期项目可以用实物期权计算价格，用于政府和项目企业间的谈判博弈.假设无风险利率为r，项目价值波动率σ.第一期项目的预期收益为

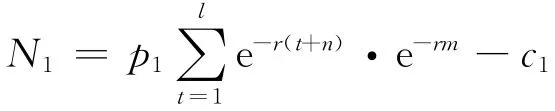
第二期项目可以看作期限时间为m的增长期权.第二期项目的投资额为c2，若折算到年初则为c2e－rm，它是期权的执行价格现值.第二期项目建成后现金收益

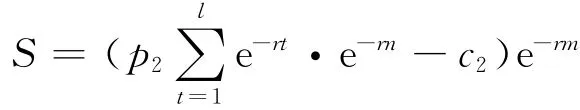
用看涨期权价值公式可以计算出第二期项目增长期权的价值C.最后，该项目总价值Pb＝N1＋C.

2 分期期权博弈模型的特许权期研究

分期期权博弈模型弥补了传统项目评价方法的缺陷，但也带来了新的挑战，譬如，这两期项目移交日期不一样，会造成运营管理上的收费混乱和政府监督的真空.

从图2可以看出，分期期权博弈模型中第一期和第二期项目移交年份不一样，而实际经营过程中，政府和项目公司往往希望该项目能够灵活选择合适的特许权期将所有项目（第一期和第二期）一起移交.这就需要缩短第二期BOT 项目的特许权期，而延长第一期BOT 项目的特许权期，如图2所示.

图2 分期BOT模式的科学选择特许权期的示意图Fig.2 Diagram of scientific choice for concession term in BOT model by stages

假设该项目第一期建成后，政府和企业验收合格后准予将第二期项目给该公司建设.观察到，第二期项目移交时间比第一期项目移交时间晚n年.假设BOT 项目第一期的特许权期延长k变成T＋k，那么第二期BOT 项目的特许权期由T变成T－（n－k）.

从而，该分期BOT 模式的实际收益用实物期权方法计算如下：

首先，第一期项目完成时在特许经营期为T＋k内 的 总 收 益 为，贴现到年初收益为扣除投资成本后，第一期项目的预期收益为

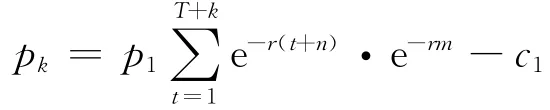
其次，第二期项目可以看作期时间为m的增长期权.第二期项目的投资额为c2，若折算到年初则为c2e－rm，它是期权的执行价格现值.第二期项目建成后现金收益为

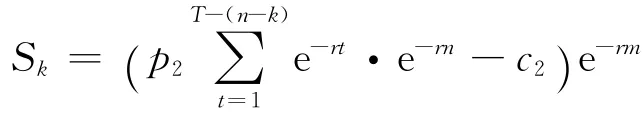
用看涨期权价值公式可以计算出第二期项目增长期权的价值qk.最后，该项目总价值Pa＝pk＋qk.

3 案例分析

某省计划修建一条从A 市经过B 市到C 市的高速公路，计划2010年初开始建设需要10 年投资42亿元人民币建成.项目采用分段BOT 模式，特许经营期为30年（不含建设期），投资方通过收取过路费收回其投资，扣除维护成本收益为2亿元·年－1.第一阶段2010年动工，修建A 市到B市的高速公路需要5年建成，总投资22亿元人民币，运营30年后2045年底转交政府运营，第二阶段2015年动工，修建B市到C市的高速公路需要5年建成，总投资20亿元人民币，运营30年后2050年底转交政府运营.假设从A 市到B市的高速公路通车后，扣除维护成本收益为1亿元·年－1，全线贯通后扣除维护成本收益为2 亿元·年－1.问：如果全线贯通后整体移交，应该选择在那一年底保证政府和企业的收益都不受损失？

该项目示意图如图3所示.

假设无风险利率按一年期国债利率1.95%计算，即r＝1.95%，项目价值波动率σ＝20%.

图3 实际项目的科学选择特许权期的示意图Fig.3 Diagram of scientific choice for concession term in practical project

分期BOT 模式的收益用实物期权方法计算如下：

记pk为第一期项目在特许经营期为T＋k内扣除投资成本后的总收益贴现到2015年初的价值，qk为第二期项目在特许经营期为T－（n－k）内扣除投资成本后的总收益贴现到2015年初的期权价值，计算结果见表1.

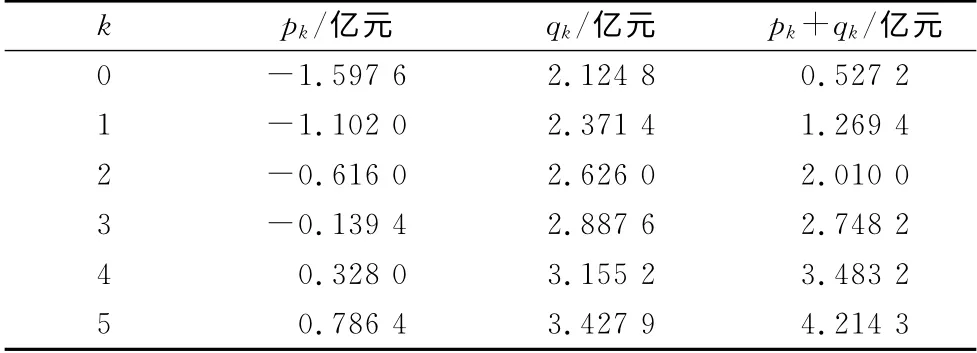
表1 特许经营期为T＋k 各期项目的收益（k＝0，1，2，3，4，5）Tab.1 Profit for every stage of BOT project when concession term is T＋k（k＝0，1，2，3，4，5）

不考虑同时移交时的收益为：Pa＝p0＋q5＝－1.597 6＋3.427 9＝1.830 3（亿元）.

如果考虑项目一期和二期同时移交，则整个项目特许经营期为T＋k的收益如表1.

针对该模型，分析如下：在不增加项目总价值的情况下，取k＝1，此时要减少部分企业利益；当k＝2时，也就是该项目第一期特许权期为32 年，第二期特许权期为27年时，该项目总价值为2.01亿元.此时，该项目对企业投资更有吸引力，这可以增加政府在项目合作初始谈判时的博弈空间.另外，政府在第一期项目结束时，可以检查项目的完成质量，以此决定是否继续与该公司合作开展第二期项目，保证公众利益最大化.

4 结论

本文对城市基础设施BOT 项目分期期权博弈模型进行了回顾，并在假设项目公司第一期项目和第二期项目与政府进行项目移交时间相同的情况下，建立了BOT 项目分期实施的一种期权博弈分析新模型，并对如何科学地确定分期期权博弈模型中的特许权期进行深入详尽的分析，最后通过实际例子计算进行了实证的分析和讨论.

该模型既能有效地保护和加强政府的利益，激励项目公司提高BOT 项目的建设质量，又考虑了政府和项目公司管理上的弹性.虽然项目公司在施工中总会有减少建设成本投入的可能性，但在政府根据项目的施工情况决定是否收回第二期投资机会的风险面前，项目公司不会做出影响工程质量的投机行为.

在本文中，没有考虑项目公司若拥有其他形式的实物期权会对城市基础设施BOT 项目特许权期产生何种影响以及如何找到增长期权对建设成本投入的直接关系，这些难点有待进一步研究.诚然，并不是所有的城市基础设施项目都存在值得重视的期权，并且实物期权模型中各个参数的确定需要不断改进，在本文中并没有深入研究.同时，对于多种期权对决策模型的影响在文中没有探讨，这些有待进一步深入研究.

［1］ 杨宏伟，周晶，何建敏.基于博弈论的交通BOT 项目特许权期的决策模型［J］.管理工程学报，2003，17（3）：93.YANG Hongwei，ZHOU Jing，HE Jianmin.Decision－making model on concession term for traffic BOT project on the basis of game theory［J］.Journal of Industrial Engineering and Engineering Management，2003，17（3）：93.

［2］ 赵立力，黄庆，谭德庆.基础设施BOT 项目的产品价格调整机制研究［J］.预测，2006，25（2）：74.ZHAO Lili，HUANG Qing，TAN Deqing.Research on price adjustment mechanism for infrastructure BOT projects’products［J］.Forecasting，2006，25（2）：74.

［3］ 李启明，申立银.基础设施BOT 项目特许权期的决策模型［J］.管理工程学报，2000，14（1）：43.LI Qiming，SHEN Liyin.Decision－making model on concession term for infrastructure BOT projects［J］.Journal of Industrial Engineering and Engineering Management，2000，14（1）：43.

［4］ 杨屹，郭明靓，危文秀.基于期权博弈的基础设施BOT 项目二阶段特许权期决策模型［J］.中国软科学，2007，6：81.YANG Yi，GUO Minliang，WEI Wenxiu.Two－stage concession term decision model for infrastructure BOT projects based on option game［J］.China Soft Science，2007，6：81.

［5］ 姜礼尚.期权定价的数学模型和方法［M］.北京：高等教育出版社，2010.JIANG Lishang.Mathematical modeling and methods for option pricing［M］.Beijing：Higher Education Press，2010.

［6］ Smith T J，Ankum L A.A real options and game theoretic approach to corporate investment strategy under competition［J］.Financial Management，1993，22（3）：241.