突发事件应急设施选址问题的模型及优化算法

丁雪枫，尤建新，2，王洪丰

（1.同济大学 经济与管理学院，上海200092；2.上海大学 管理学院，上海200444；3.德州学院 计算机系，山东 德州253023）

近年来，世界上频繁发生各种大规模的自然灾害事件和人为灾害事故，造成了大量的人员伤亡及经济损失［1］.对重大突发紧急事件的应对策略管理研究必将成为我国政府和学术界的研究热点，其中救援设施系统的优化是关键问题之一.应急系统要在有限的时间和建筑空间的条件下发挥防灾减灾作用，尽可能多、快地抢救受灾人员，实现时间空间的最优化，同时还要尽量节约转移成本，降低生命财产损失，提高整个应急救援系统的服务质量与效率［2］.因此，研究重大突发事件救援设施系统优化具有十分重要的现实意义，有利于促进和实现城市空间的真正的可持续发展［3］.目前针对重大突发事件救援设施系统模型的建立，大多以紧急救援应对时间和成本为衡量标准［4］，主要研究成果包括：徐波等人提出将城市分为3个层次，在此基础之上给出了疏散道路宽度与人流密度、疏散人口数量的动态优化模型［3］；张玲等人提出按照灾区分组及场景分析的方法确定两种级别的应急物资分配的多目标规划模型［5］；唐伟勤等人提出将应急物资分为3个阶段，设计并揭示了大规模突发事件应急物资调度的全过程模型，该模型为大规模突发事件应急物资调度决策提供了理论依据和方法指导［1］；陈志宗和尤建新对重大突发事件应急救援设施选址的特点进行了分析，提出基于公平与效率原则的城市避难所选址多目标规划模型，该模型整合了传统选址模型中常用的最大覆盖模型、p－中心模型与p－中值模型，可适应不同的部署策略［6－7］；计国君等从可重复利用物资和不可重复利用物资角度考虑，建立了救援物资与机会成本对应关系的应急物资配送整数规划模型［8］，对模型的求解方法研究主要包括方磊和何建敏提出的基于分支定界法的求解算法［9］；刘红娟等人提出的基于遗传算法求解应急物流多设施选址模型的方法［10］；王文峰等人提出的基于分布估计算法的启发式模型求解方法［11］；韩强提出的基于模拟退火算法的多目标应急设施选址问题求解方法［12］等.突发事件应急管理具有低概率性和低频率性、对应急管理服务需求的突发性和应急管理反应的高时效性，应急救援物资的高需求量，应急服务与救援物资消耗的持续性等特点［12］.一个城市对于发生重大灾难之后所做出的应急反应可以体现该城市对发挥可利用资源和成本效用的管理能力［13］，救援管理的一个关键环节就是在灾害事件发生后，迅速地从应急设施服务站将救急物资转移至灾害现场展开救援工作，应急设施选择地点的合适与否将直接影响到应急管理的好坏.

模拟植物生长算法（plant growth simulation algorithm，PGSA）是一种新型智能优化算法，该算法是基于分形领域和计算机图形学模拟植物生长过程的分支模型系统演化而来的.模拟植物生长算法对参数设置没有依赖性，对目标问题的求解也没有过多的限制要求.本文以重大突发事件救援设施选址问题为研究目标，考虑距离、成本等多方面因素对问题建立数学描述模型，并采用模拟植物生长算法对实例进行求解，结果验证了算法的有效性和优越性.

1 模型

应急救援设施选址问题实际上可归结为点覆盖问题，因此属于NP－hard问题［4］.这里暂不考虑有外界援助，假设重大突发事件不会同时在多个地区发生.灾难发生之后的一段时间可利用的救援物资全部来自救援设施点，并允许多个应急救援服务点联合救援，对于设施选址的设置衡量标准从两个方面考虑，一是应急的时间，二是救急设施点的消耗成本，包括建设成本和救援成本.重大突发事件救援设施选址问题可以描述为：假设有n个潜在可能的突发事件发生点（救援需求点），每个救援需求点表示为j（j＝1，2，…，n），有m个候选的应急设施服务点，各服务点i的建设成本为ri，每次的救援成本为ci（i＝1，2，…，m），从应急设施服务点i到达突发事件发生点j的距离为dij，要找出一个最佳的救援配置方式，使得最短时间内损失的总成本也能够达到最小.

为了便于讨论，现将使用到的模型参数介绍如下：n为突发事件发生点的个数；m为候选应急设施服务点的个数；wj为救援需求点j的权重；dij为应急设施服务点i与救援需求点j之间的距离；ri为应急设施服务点i的建设成本；cij为应急设施服务点i至救援需求点j的运输成本；tij为应急设施服务点i至救援需求点j运输量；p为预先确定的应急救援设置服务点的个数；qj为救援需求点j要求的最少救援设施服务点个数；xi为值为0或者1，如果候选应急设施i被选中设立，则xi值为1，否则，xi值为0；yij为值为0或1，如果应急设施服务点i参加救援需求点j的救援工作，则yij的值为1，否则，值为0（i＝1，2，…，m，j＝1，2，…，n）；F1，F2，F3为多目标优化函数.

则重大突发事件设施选址问题的模型可建立为

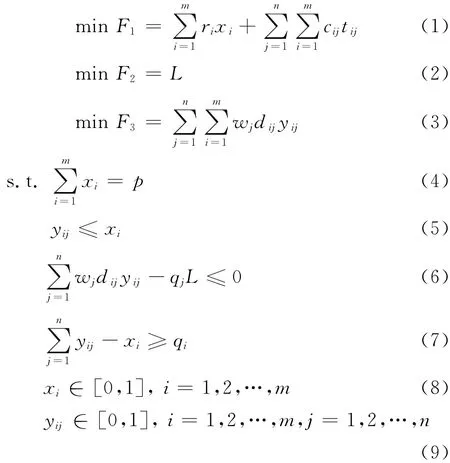
式（1）表示建立应急设施服务点的总成本最小；式（2）和约束条件（6）表示将各候选应急设施服务点到达各个救援需求点的最大距离最小化，体现了应急设施建立的公平性；式（3）表示各候选应急设施服务点到达各个救援需求点的总加权距离最小，体现了应急设施的效率性；约束条件（4）和（5）保证了参加救援需求点救援工作的应急设施服务点不超过p个；约束条件（6）保证了选中设置的应急救援服务点个数不小于救援需求点j所要求的最少设施个数qi.

该模型是一个多目标规划模型.这里，将重大突发事件设施选址问题的决策变量设为xi，应急服务点是否参与救援任务是通过yij来进行判断，yij的值为0或者1，其中1表示应急服务点被选中参与救援工作，0表示没有选中.由于不同目标偏好下，被选择的权重决策也有不同，同时为了便于模型的求解，可以采用线性加权的处理方法，将多目标规划模型转化为单目标模型来进行求解，即针对各个目标子问题，给出各自的重要程度系数，可以表示为λ1，λ2，λ3，且λ1＋λ2＋λ3＝1.则应急设施选址问题的多目标函数可以表示为

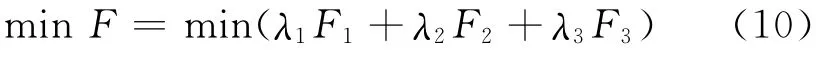
2 算法

2.1 模拟植物生长算法动力机制

生物学中将植物可以生长出新茎枝的部位称为生长点.植物先由种子生长出第一个茎枝，如果植物的生长点多于一个，则可继续生长新枝干的生长点由生长点的形态素浓度决定，植物的生长过程是一个由根生茎，茎生枝，枝生枝的反复迭代的过程.研究证实，植物上形态素浓度值大的生长点较浓度小的生长点具有优先生长机会，而植物形态素浓度的大小主要由植物的向光性决定，同时，植物各个茎和枝干的形态素浓度随着环境位置的变化在生长出新枝后会在各生长点之间重新分配.假设茎杆长度表示为M，上面有K个初始生长点SM＝（SM1，SM2，…，SMK），其各自的形态素浓度值 是PM＝（PM1，PM2，…，PMK）；设在单位长度为m（m＜N）上的生长点为Sm＝（Sm1，Sm2，…，Smq），其各自的形态素浓度值是Pm＝（Pm1，Pm2，…，Pml），则给出茎和枝上的生长点形态素浓度值计算公式为［16－17］

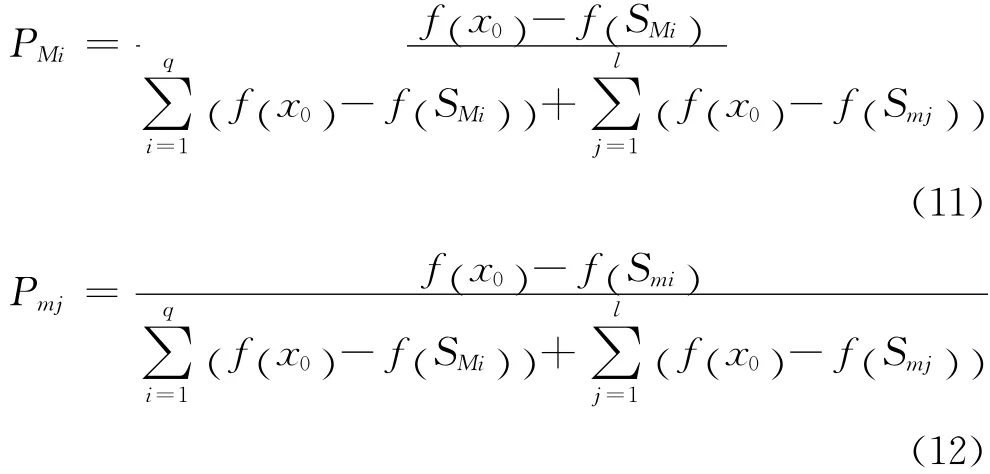
式（11）和（12）中：x0表示初始原点，即植物的根；f（·）是生长点的反受光函数，f（·）的函数值随着生长点的光照条件越好而变小，这真实描述了各个生长点形态素浓度值与其各自点的光照条件与原点处光照条件的相对应关系.由式（11），（12）不难得出，一棵植物包含的所有生长点，其形态素浓度相加之和为1（图1），即

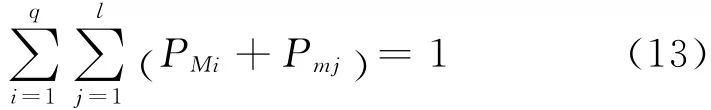
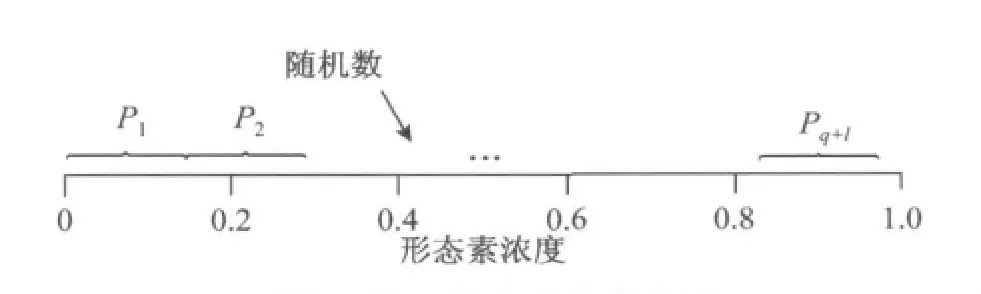
图1 形态素浓度状态空间Fig.1 Morphactin concentration state space

根据式（11），（12）可以求得各个生长点的形态素浓度，形态素浓度确定之后，随机生成一个［0，1］间的数字，用来确定下一轮长出新枝干的生长点，这就好比是在［0，1］区间内投掷小球，球落入哪个状态空间，则该空间对应的生长点就是下一轮生长新枝干的生长点（图1）.随着新枝的生成，k和l的值也会随之变化，每一轮生长之后，该轮作为生长点的元素将从生长集合中删去，新生长出来的枝干上的生长点将被加入到生长集合中，重复上述步骤，直到没有新枝生成为止，这样最后就得到了一株完整的植物.

2.2 重大突发事件救援设施选址问题的模拟植物生长算法

利用模拟植物生长算法求解重大突发事件救援设施选址问题，实际上就是模拟植物枝干长满整个生长空间的过程，根据植物生长的内在动力及向光性的作用力，建立茎、枝干繁殖生长及凋谢的动力机制，将植物的整个生长空间看作解的可行域，光源当作全局最优解，植物的动力生长机制由其向光性决定，根据植物学中的形态素浓度理论建立不同光线强度的环境下按照全局最优的方式向着光源快速生长的动力模型［14－16］.

2.2.1 决策变量的设定

这里，将重大突发事件救援设施的选址问题的决策变量设计为一个布尔向量（x1，x2，…，xm）.这种设定方式是比较合理的，若元素值为0，则表示该候选应急设施服务点没有被选中；若元素值为1，表示该候选应急设施服务点被选中进行设置.当重大突发事件发生之后，所设置的应急设施服务点参加哪一个救援需求点的救援工作由yij来进行判断，yij同样也是取布尔值，若yij的值为0，则表示应急设施服务点i不参与救援需求点j的救援工作；若yij的值为1，则表示应急设施服务点i参与救援需求点j的救援工作.

2.2.2 终止判定的依据

为了提高算法的计算效率及收敛速度，同时保证算法的计算质量，这里将搜索终止的判定依据按如下方法设计：①模拟植物生长算法搜索目标问题最优解的过程中，其搜索范围是植物的整个生长空间，如果按照搜索步长1进行搜索，这样的搜索虽然会找到全部最优解，但是当生长空间较大时，就会耗费较长的搜索时间.因此，可以考虑将算法的搜索步长先设定为一个较大的值，如果搜索不到最优解，则将步长逐渐减小继续搜索，如此反复，直到步长为1停止，步长的初值一般可设为2n.②在搜索最优解的过程中，为了避免还没找到最优值提前退出搜索，和最优解已经找到但是搜索动作还在继续的情况，可以通过设定循环迭代的最大次数和解重复出现的最大次数的方法，如果搜索最优解的过程中，当前的搜索迭代次数已经达到了所设定的循环迭代最大次数，或者当前求得的最优解重复出现的次数达到了所设定的次数上限，那么就认为该解是问题的最优解，搜索操作停止.

2.2.3 约束条件的解决方法

针对重大突发事件救援设施选址问题模型中约束条件各自的特点，对各约束条件的处理方式：①对于约束条件式（4），应急设施服务点的设置个数的限定，是通过采用设定决策变量的取值范围来限制，在实际采用模拟植物生长算法求解中，该操作对应表现为对植物的茎、枝干上的生长长度进行限定.在此基础之上，根据约束条件式（5）和（7），对植物茎、枝干上的每个可行解进行搜索，来完成设置服务点参与救援工作的服务点个数之间分配关系的确定.②为保证所设置的应急救援设施服务点的最大距离L最小化，满足了对应急救援设施服务点快速反应的要求，算法中是通过对约束条件式（6）校核来实现的.

基于模拟植物生长算法的重大突发事件救援设施选址问题具体算法步骤如下：

步骤1 确定一个初始解x0，为了提高初始解的质量，并且保证初始解的一般性，使得初值尽可能地与最优解接近，因此可以采用贪心法随机生成的方式来生成.初始化最佳值变量Xmin＝x0，初始化最佳值函数Fmin＝f（x0）.设定最大迭代次数、解重复出现最大次数的大小.

步骤2 搜索新生长点，从种子节点x0开始生长，xi取值范围在［0，ki］之内，沿着各个坐标轴的正负方向按照步长作与坐标轴平行的直线段，在各个线段上搜索可能的新生长点.选择一个优先生长点，从优先节点开始，若搜索到的可能生长点不在生长空间范围之内，或者不符合生长条件，则剔除该节点，若步长＞1，步长＝步长－1；否则，比较基点函数值与生长点的目标函数值大小，若生长点的目标函数值大于基点函数值，则将该点删除，否则将该点加入到生长点集合中.

步骤3 保留目标函数的最优解，从生长点集合中选取与基点函数值差值最大的节点，比较新的生长点的函数值与Fmin中函数值的大小，若新的生长点的函数值大于Fmin的值，保持Fmin，Xmin中的值不变；若新的生长点的函数值等于Fmin的值，则保留该生长点，将其放入生长点集合；若新的生长点的函数值小于Fmin中的值，则更新Fmin值为新的生长点函数值，Xmin更新为新生长点的下标值，同时将旧的生长点从生长点集合中删除，新的生长点向其2n个方向生长出新枝.

步骤4 判断是否满足搜索终止的条件，若循环次数达到设定的最大迭代次数或者最优解连续保持最大重复次数不变，则按式（11），（12）分别计算茎、枝干上每个生长点的形态素浓度值；否则，搜索结束.

步骤5 建立［0，1］间的概率空间，即Pi＋1＝

步骤6 生成一个［0，1］随机数.

步骤7 如随机数是在（Pi，Pi＋1］之间的某个数，则该数所对应的生长点就是下一个新生长点.

步骤8 若最优值变量的值重复出现达到了所设定的最大值重复出现次数都没有新的树枝产生，或者循环迭代的次数达到了设定的最大迭代次数，则生长过程结束；否则，返回步骤2.

步骤9 返回Xmin，Fmin的值.

3 实例

为了验证本文设计的模型及求解算法合理性和有效性，这里针对一个具体实例，根据上面所设计的突发事件救援设施选址问题的多目标规划模型，以及模拟植物生长算法来对实例进行计算，并将结果与通用性较强的遗传算法计算所得的结果进行比较.

算例 考虑某地区的15个街区，假设各个街区的需求都集中在街区的中心（救援需求点），当地政府计划在9个候选应急救援设施服务点（x1，x2，x3，x4，x5，x6，x7，x8，x9）中选择p＝6个地点来设置应急救援设施服务点.各个候选应急救援设施服务点到达各个救援需求点之间的距离以及各个需求点处的人口数量如表1所示.各个候选应急救援设施服务点的建设成本与运输成本如表2所示.当地政府要求5万人以下的街区至少有1个应急设施救援服务点参与其救援工作，5万～10万人的街区至少有2个应急救援设施服务点参与其救援工作，10万人以上的街区至少有3个应急救援设施服务点参与其救援工作.

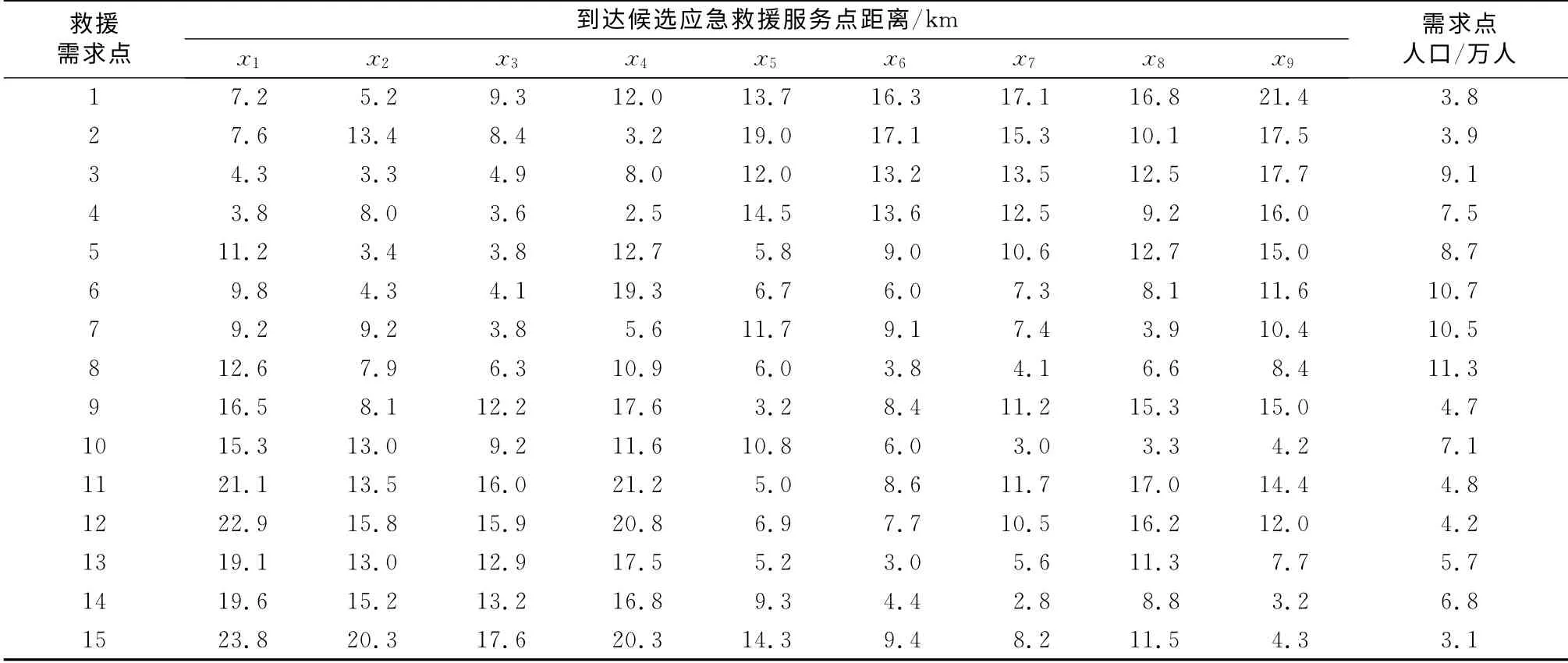
表1 各候选应急救援设施服务点到达救援需求点的距离及救援需求点人口数量Tab.1 Distances from each candidate service points to the needed emergency rescue points and the needed emergency rescue points’population quantities

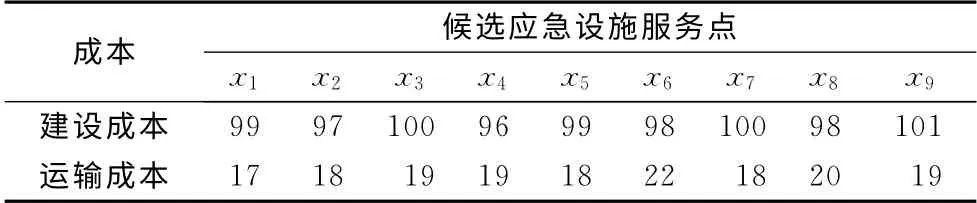
表2 各候选应急救援设施服务点的建设成本与运输成本Tab.2 Construction cost and transportation cost of each candidate service points 万元

每个街区的人口数量当作该街区的权重，由算例可得：q1＝q2＝q9＝q11＝q12＝q15＝1，q3＝q4＝q5＝q10＝q13＝q14＝2，q6＝q7＝q8＝3；各个候选应急救援设施服务点到达各需求点的最大距离向量L＝（23.8，20.3，17.6，21.2，14.5，17.1，17.1，17，21.4）；从效率性及公平性的方面优先考虑，这里将式（10）中的权重因子分别取值为：λ1＝0.2，λ2＝0.4，λ3＝0.4.

采用模拟植物生长算法对该算例进行计算，所得决策变量的最优解为：（0 1 1 1 1 0 1 0 1），即x2，x3，x4，x5，x7，x96个服务点被选定作为该地区的应急救援设施服务点，最优解下所求得的最优距离为1 068.88km.各被选定的应急救援服务点所负责的服务救援需求点yij的计算结果分别为：y2j＝（1 0 1 0 1 1 0 0 0 0 0 0 0 0 0），y3j＝（0 0 1 1 0 1 1 1 0 0 0 0 000），y4j＝（0 1 0 1 0 0 1 0 0 0 0 0 0 0 0），y5j＝（00 0 0 1 1 0 1 1 0 1 1 1 0 0），y7j＝（0 0 0 0 0 1 1 1 0 1 0 0 1 1 0），y9j＝（0 0 0 0 0 0 0 0 0 1 0 0 0 1 1）.即应急救援设施服务点x2参与救援需求点1，3，5，6的救援工作，应急救援设施服务点x3参与救援需求点3，4，6，7，8的救援工作，应急救援设施服务点x4参与救援需求点2，4，7的救援工作，应急救援设施服务点x5参与救援需求点5，6，8，9，11，12，13的救援工作，应急救援设施服务点x7参与救援需求点6，7，8，10，13，14的救援工作，应急救援设施服务点x9参与救援需求点10，14，15的救援工作.采用遗传算法对该算例进行计算，所得的最优解为（1 1 1 0 1 0 1 0 1），所得的最优距离为1 438.38km.表3给出了模拟植物生长算法和遗传算法的计算结果对比情况.

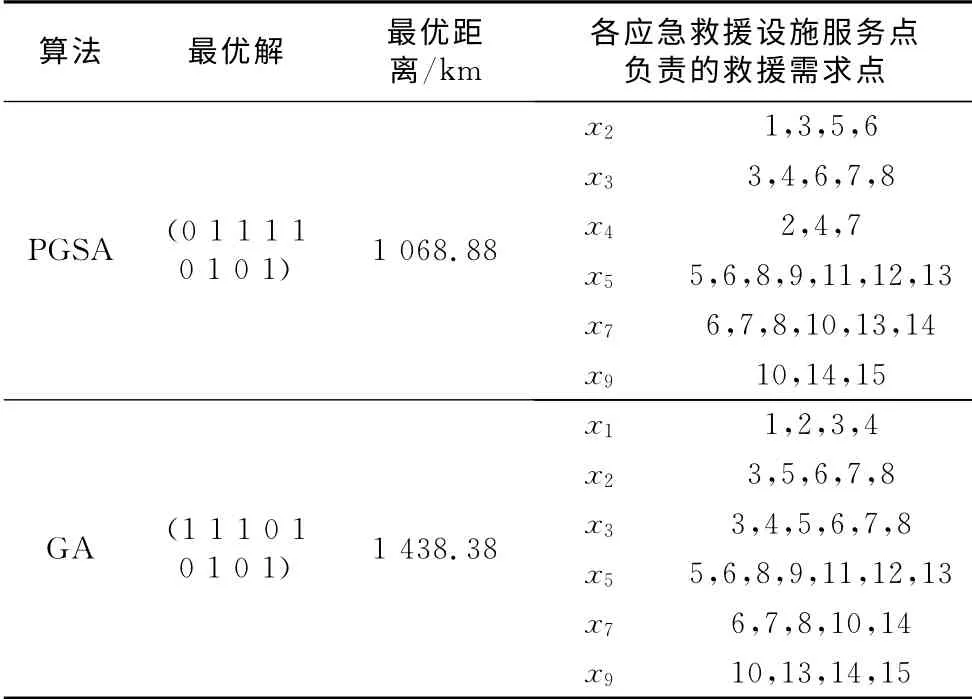
表3 PGSA 与GA 的计算结果对比情况Tab.3 Computing result comparison between PASA and GA

由表3显示，本文提出的模拟植物生长算法求解重大突发事件救援设施选址问题的模型所得的最优解较遗传算法所得的最优解有很大提高，最优总距离较遗传算法的结果有了很大的减少，同时在应急救援设施服务点负责救援需求点的分配上也较遗传算法有了改进，精简了冗余节点，提高了解的质量，结果验证了本文算法具有良好的性能.

4 结语

在建立重大突发事件应急救援设施选址问题的模型时，充分考虑了公平性、效率性、建立成本等因素，本文所建的应急设施选址问题模型整合了常用的最大覆盖模型、p－中值模型与p－中心模型.对于模型的求解，采用一种新型的智能优化算法——模拟植物生长算法来实现，该算法可以实现在全局范围内快速地搜索最优解，并且算法设计简单、易于实现，对目标函数及参数设置都没有过多的限制要求，通过对实例的计算，结果验证了本文算法具有较优的性能.

［1］ 唐伟勤，张敏，张隐.大规模突发事件应急物资调度的过程模型［J］.中国安全科学学报，2009，19（1）：33.TANG Weiqin，ZHANG Min，ZHANG Yin.Process Model for materials dispatching in large－scale emergencies［J］.China Safety Science Journal，2009，19（1）：33.

［2］ 徐琴，马祖军，李华俊.城市突发公共事件在应急物流中的定位－路径问题研究［J］.华中科技大学学报，2008，22（6）：36.XU Qin，MA Zujun，LI Huajun.Location－routing problem in emergency for public emergencies［J］.Journal of Huazhong University of Science and Technology，2008，22（6）：36.

［3］ 徐波，关贤军，尤建新.城市防灾避难空间优化模型［J］.土木工程学报，2008，41（1）：93.XU Bo，GUAN Xianjun，YOU Jianxin.The optimization models of urban disaster prevention space［J］.China Civil Engineering Journal，2008，41（1）：93.

［4］ 韩强.多目标应急设施选址问题的模拟退火算法［J］.计算机工程与应用，2007，43（30）：182.HAN Qiang.Simulated annealing algorithm for multi－object emergency location problem［J］.Computer Engineering and Applications，2007，43（30）：182.

［5］ 张玲，黄钧，朱建明.应对大规模突发事件的资源布局模型与算法［J］.系统工程，2008，26（9）：26.ZHANG Ling，HUANG Jun，ZHU Jianming.The location and allocation model and algorithm of response to large－scale emergency［J］.System Engineering，2008，26（9）：26.

［6］ 陈志宗，尤建新.重大突发事件应急救援设施选址的多目标决策模型［J］.管理科学，2006，19（4）：10.CHEN Zhizong，YOU Jianxin.A multi－objective decision model of emergency rescue facility location for large－scale emergency incidents［J］.Management Science in China，2006，19（4）：10.

［7］ 陈志宗，尤建新.城市防灾减灾设施的层级选址问题建模［J］.自然灾害学报，2005，14（2）：131.ZHANG Zhizong，YOU Jianxin.A modeling approach to hierarchical location problem of urban disaster prevention and mitigation facilities［J］.Journal of Natural Disasters，2005，14（2）：131.

［8］ 计国君，朱彩虹.突发事件应急物流中资源配送优化问题研究［J］.中国流通经济，2007，21（3）：18.JI Guojun，ZHU Caihong.Study on the distribution optimal problem in emergency logistics for emergency event［J］.China Business and Market，2007，21（3）：18.

［9］ 方磊，何建敏.城市应急系统优化选址决策模型和算法［J］.管理科学学报，2005，8（1）：12.FANG Lei，HE Jianmin.Optimal location model and algorithm of urban emergency systems［J］.Journal of Management Sciences in China，2005，8（1）：12.

［10］ 刘红娟，罗挺，姜玉宏，等.基于遗传算法的应急物流多设施选址模型研究［J］.后勤工程学院学报，2010，26（3）：46.LIU Hongjuan，LUO Ting，JIANG Yuhong，et al.Study of multi－facility location model for emergency logistics based on genetic algorithm ［J］.Journal of Logistical Engineering University，2010，26（3）：46.

［11］ 王文峰，郭波，刘新亮.多级覆盖设施选址问题建模及求解方法研究［J］.中国管理科学，2007，15（z1）：144.WANG Wenfeng，GUO Bo，LIU Xinliang.Model and solution approach for multiple－quality－of－coverage facility location problem［J］.Chinese Journal of Management Science，2007，15（suppl.）：144.

［12］ Gwyndaf Williams，Stuart Batho，Lynne Russell.Responding ro urban crises：the emergency planning response to the bombing of Manchester city centre［J］.Cities，2000，17（4）：293－304.

［13］ Drezner Z，Hamacher H W.Facility Location Applications and Theory［M］.Berlin：Springer Verlag，2002.

［14］ 杨丽徙，王锴，黄训诚，等.应用模拟树木生长算法求解无功优化问题［J］.郑州大学学报：工学版，2008，29（2）：69.YANG Lixi，WANG Kai，HUANG Xuncheng，et al.Application of trees growth simulation algorithm to solve reactive power optimization problem［J］.Journal of Zhengzhou University：Engineering Scinece，2008，29（2）：69.

［15］ 李彤，王春峰，王文波，等.求解整数规划的一种仿生类全局优化算法——模拟植物生长算法［J］.系统工程理论与实践，2005，25（1）：76.LI Tong，WANG Chunfeng，WANG Wenbo，et al.A global optimization bionics algorithm for solving integer programming—plant growth simulation algorithm［J］.Systems Engineering—Theory and Practice，2005，25（1）：76.

［16］ 李彤，宿伟玲，李磊.单级与二级整数规划算法原理及应用［M］.北京：科学出版社，2007.LI Tong，SU Weiling，LI Lei.Single level and bilevel integer programming algorithm theory and its application［M］.Beijing：Science Press，2007.