面向输出性能的微加速度计建模与拓扑优化

刘广军，姜 涛

（同济大学 机械与能源工程学院，上海201804）

加速度计是惯性导航、惯性制导和控制检测设备的重要测量元件，用来测量载体的运动加速度［1］.采用MEMS（micro－electro－mechanical systems）技术加工的电容式硅微加速度计具有结构简单、功耗低、成本低、噪声特性好、漂移低等诸多优点，已成为当前研究的热点和主流［2］.当前针对微加速度计结构设计的研究集中在两个方面［2－5］：一是通过直接制作微加速度计原型来验证设计，此种方法耗费大量时间与经费；二是针对微加速度计结构的尺寸优化来提高其灵敏度，但这种方法的效率较低，且存在着不能变更结构拓扑的缺陷.

通过微加速度计结构拓扑的创新与优化来改善性能，一直是微结构设计的一大难题，原因是微结构的拓扑形态决定了微结构的功能、载荷、约束和材料配置等的适用范围，对微加速度计结构拓扑的设计与优化研究，尚存很大的研究空间［6］.

为此，本文以一种MEMS技术制备的电容式谐振微加速度计为研究对象，建立微加速度计检测电容为输出性能的计算模型，实现面向微加速度计最终输出性能——检测电容的动力学特性与检测特性的分析；为提高微加速度计的输出性能，建立了拓扑优化数学模型，根据拓扑优化流程进行了微加速度计结构拓扑优化，并以算例说明所提方法的有效性.

1 微加速度计的工作原理与输出性能建模

1.1 微加速度计的结构与工作原理

微加速度计的结构如图1a所示.该微加速度计为“三明治”结构，为了提高检测精度，采用差动电容检测.整个微加速度计结构由上下两块玻璃板和中间的硅片组成，上下玻璃板上各有1块检测电容，如图1b所示.工作时，中间的敏感质量块在加速度作用下往一侧偏移，此时差分检测电容由于极板距离发生变化而改变，通过检测差分电容的变化量，可以得到系统的加速度.

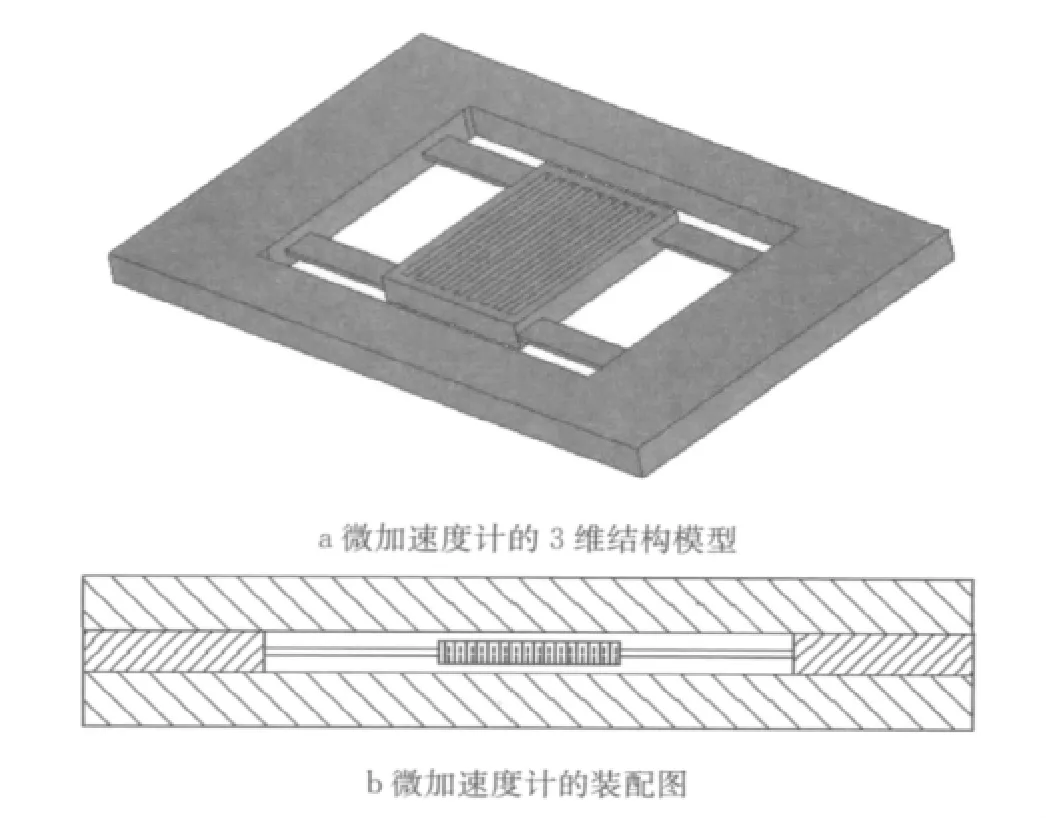
图1 微加速度计的结构示意图Fig.1 Schematic drawing of the micro－accelerometer

1.2 微加速度计的输出性能建模

微加速度计依靠电容输出检测加速度，因而需要明确输出性能——检测电容的计算方法，解析面向微加速度计最终输出的动力学特性与检测特性.微加速度计最终的电容输出性能模型，即检测电容的检测特性与其微结构之间的动力学模型，是后续分析和优化的基础.

当系统有加速度作用时，微加速度计中间的敏感质量块在加速度作用下往一侧偏移，如图2所示.由模态分析可知，微加速度计的第1阶振动模态为其工作模态，固有频率为12 443 Hz，第2，3，4阶模态的固有频率分别为18 814，34 281，51 685Hz.

图2 微加速度计的工作状态Fig.2 Working state of the micro－accelerometer

微加速度计的基本数学模型是一个质量—弹簧—阻尼系统，加速度通过敏感质量形成惯性力作用于系统.对于该力学模型，可列出如下2阶微分方程：

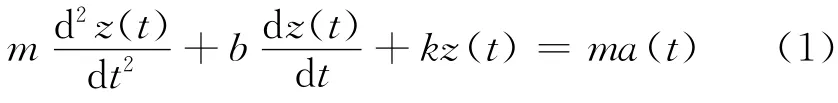
式中：m为质量；b为黏性阻尼系数；k为弹性刚度；t为时间；z（t）为敏感质量块相对微加速度计固定端的位移；a（t）为输入的加速度.

根据振动理论，当微加速度计处于常加速度输入下的稳态时，其敏感质量块相对固定端的位移z趋于稳态值：

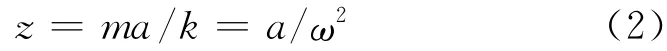
式中ω为微加速度计的第1阶固有频率.

当加速度a＝0时，敏感质量块位于平衡位置，两差动电容C1和C2相等，即

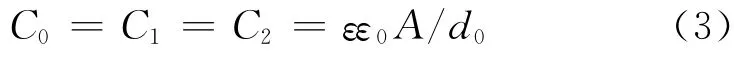
式中：C0为C1和C2的静态初始电容；ε0为真空介电常数；ε为介质的相对介电常数；A为电容极板面积；d0为电容极板标称间距.

当存在加速度时，敏感质量块由于加速度造成的微小位移可转化为差动电容的变化，且两电容的差值与位移量成正比，双边电容相对变化量ΔC与C0存在如下关系：

将式（2）代入式（4），可得输入加速度a和双边电容变化的关系为

因此，不同的加速度输入可对应不同的电容变化，输出电容与加速度呈正比关系.将电容变化通过检测电路转换成电信号，就可以用这个电信号来表征被测加速度的大小.由式（5）可得输出检测电容相对输入加速度的灵敏度k为

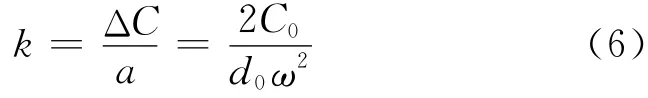
灵敏度是微加速度计的最重要性能指标之一，一般希望微加速度计以高灵敏度方式工作，要求其输出电容最大化.

2 微加速度计的结构拓扑优化算法

2.1 微加速度计的结构拓扑优化流程

为使微加速度计具有更好的性能，即具有更高的灵敏度和稳态输出，对微加速度计的结构拓扑进行优化.目前的拓扑优化算法有多种，包括基结构法、遗传算法、渐进结构法、水平集方法、均匀化方法、相对密度法等.基结构法和遗传算法适用于离散结构.渐进结构法则缺乏严密的数学论证，严重依赖有限元软件，且不能保证总能获得最优解.水平集方法存在边界演化停滞问题，且计算效率较低.相对密度法受均匀化方法的启发而产生，以密度为拓扑设计变量，将结构拓扑优化问题转化为材料的最优分布问题，是微型结构拓扑优化中一种较为有效的物理描述方法，故采用相对密度法对微加速度计的结构拓扑进行优化.

相对密度法引入一种假想的相对密度在0～1之间可变的材料，优化时以密度为拓扑设计变量，这样结构拓扑优化问题就转化为材料的最优分布问题.相对密度法的材料模型如下：

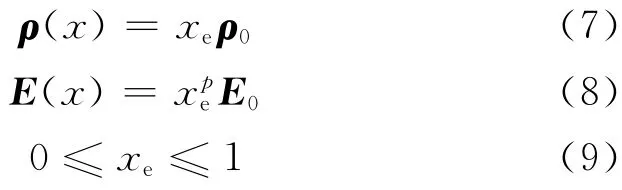
式中：ρ和E分别为所选材料的密度矩阵和弹性矩阵；ρ0和E0分别为均质实体的密度矩阵和弹性矩阵；x为设计变量；xe为单元的相对密度；p为惩罚因子.

采用相对密度法进行结构拓扑优化会出现棋盘格现象，因而需对原始拓扑图进行过滤，这里采用Diaz和Sigmund等人提出的过滤求解技术［7－8］.微加速度计的拓扑优化流程如图3所示.

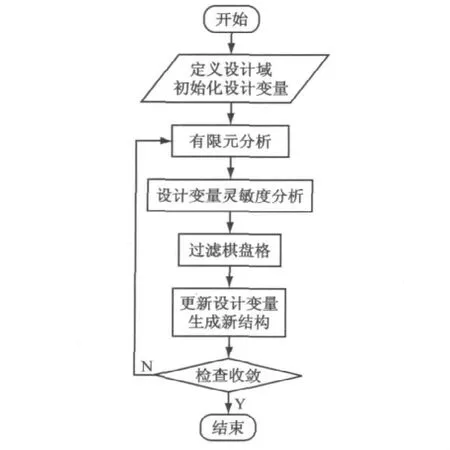
图3 微加速度计的拓扑优化流程图Fig.3 Flow chart of topology optimization of the micro－accelerometer

2.2 输出性能最大化的目标函数

由式（5）和式（6）可知，为提高微加速度计的灵敏度，就必须增加检测电容输出，因此，优化的理想目标为微加速度计的差分输出电容ΔC的最大化，即

微加速度计依靠弹性变形实现电容输出，由式（4）可知，输出电容ΔC与微陀螺敏感质量块的z向位移呈正比关系，故增大输出位移等同于增加微加速度计的灵敏度.同时，微加速度计的输出位移越大，其柔度越大.结构的柔度一般用互应变能来表征，则灵敏度最大的优化问题可转化为互应变能QMSE最大的优化问题，即

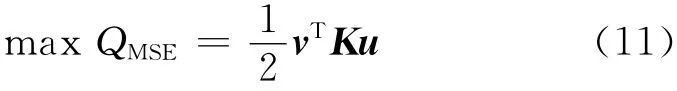
式中：v为单位载荷作用下的节点位移矩阵；K为整体刚度矩阵；u为实际载荷作用下的节点位移矩阵.

只追求输出位移的最大化，会使微加速度计的结构柔度增大，刚度变小，这样会大大减小结构的负载能力和抗冲击能力，所以拓扑优化的另一个目标是需要保证微结构的刚度和负载能力.刚度可用应变能QSE衡量，使结构刚度最大化的目标函数可表示为

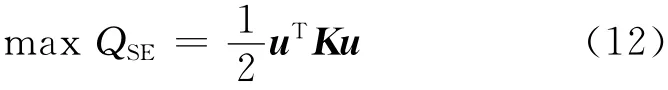
互应变能和应变能是两个此消彼长的目标，二者之间需要合适的平衡，则综合式（11）和式（12），可得微加速度计拓扑优化的目标函数为

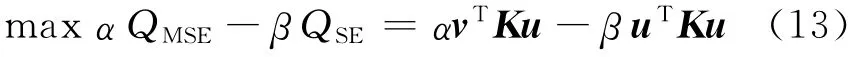
式中：α和β为权重系数，且满足α＋β＝1.

以单元密度或厚度xi（i＝1，2，…，n）为设计变量，则可对目标函数进行进一步简化［9］，由式（13）可得目标函数为

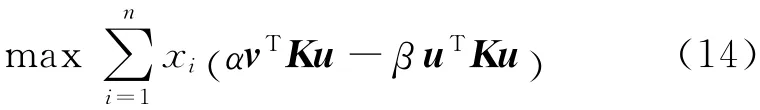
把式（14）对设计变量xi求导，可得目标函数的灵敏度Se为

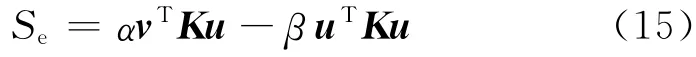
2.3 考虑频率约束的目标函数与约束条件

为避免耦合，约束条件还应考虑频率约束，使优化后的第1阶固有频率f1尽量远离第2阶固有频率f2.在拓扑优化过程中，当其中一个阶次的频率达到较大时，其他阶次的频率会降到一个较低的值［10］，因此可采用增加微加速度计第2阶固频的方法来实现增大频率差的目的.考虑频率约束的设计变量迭代公式可写为［11］

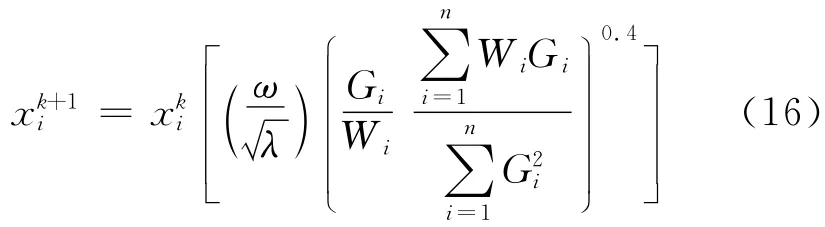
式中：k为迭代次数；Wi为单元重量系数；ω为频率低限；λ为结构的特征值；Gi为频率梯度.

拓扑优化过程中，各阶模态可能会调换次序，因此需要限制微加速度计的第1阶振型不变，故约束条件考虑如下模态性能约束：

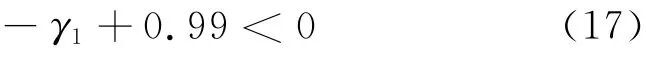
式中，γ1为微加速度计的第1阶振动模态的模态参与因子.

式（17）保证在拓扑优化过程中，微加速度计的振动模态型式不会发生改变.

2.4 目标函数的综合协调

考虑到多目标优化问题，对输出电容和频率目标函数得到的设计变量进行综合协调.假设输出电容目标函数和频率目标函数得到的更新的设计变量分别为xci和xfi，协调后新的设计变量xnewi可写为［11］

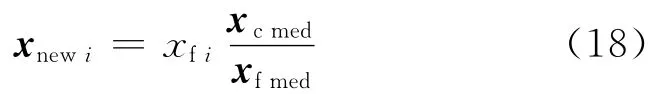
式中med表示对向量取中间值.

合并xci和xnewi，则可得到最终的设计变量xi.

3 微加速度计的结构拓扑优化算例

以图1所示的微加速度计结构为对象，采用以上所提出的拓扑优化算法，讨论微加速度计的结构拓扑优化问题.

3.1 拓扑优化对象与初始条件

微加速度计是谐振型器件，实施检测的弹性变形由弹性梁来保证，因而弹性梁结构对系统的动力学性能有着至关重要的作用.弹性梁能够传递振动，缓解冲击，影响系统的耦合特性，并能释放残余应力.弹性梁结构在很大程度上决定了微加速度计的动力学性能，因而弹性梁也就决定了微加速度计的振动模态、灵敏度和稳态输出.

图1所示的微加速度计有4 个弹性梁，连接着敏感质量块和固定质量块，呈对称形式分布，起着极其重要的连接和传递作用，是微加速度计最关键的结构之一.因此，选择微加速度计的弹性梁结构的拓扑优化作为算例，初始条件如表1所示.

表1 拓扑优化初始条件Tab.1 Initial conditions of topology optimization

3.2 拓扑优化结果与讨论

根据建立的设计变量更新公式和图3所示的拓扑流程图，对微加速度计的弹性梁进行拓扑优化，得到拓扑优化过后的材料分布图如图4所示.

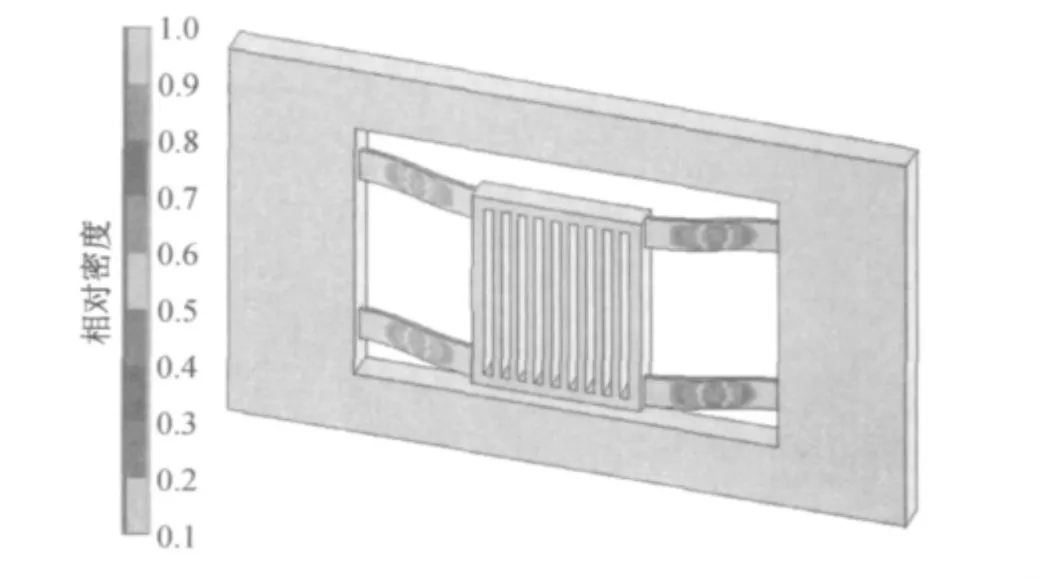
图4 拓扑优化后的微加速度计材料分布图Fig.4 Material distribution of the micro－accelerometer after topology optimization

拓扑优化所得的结构是非光滑锯齿状跳跃边界的几何模型，加工的难度非常大，故需重新处理拓扑优化结果的材料分布，并尽可能简化结构以利于加工.处理后的模型如图5所示.

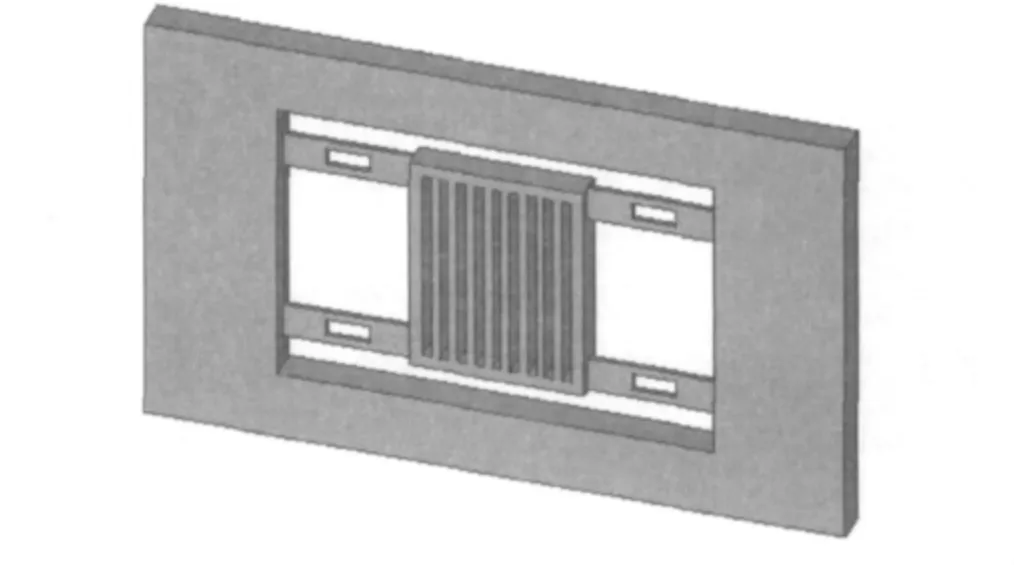
图5 拓扑优化结果处理后的模型Fig.5 The model after result processing of topology optimization

按图5的模型对微加速度计的模态和输出性能进行分析，得到的对比结果分别如表2和表3所示.

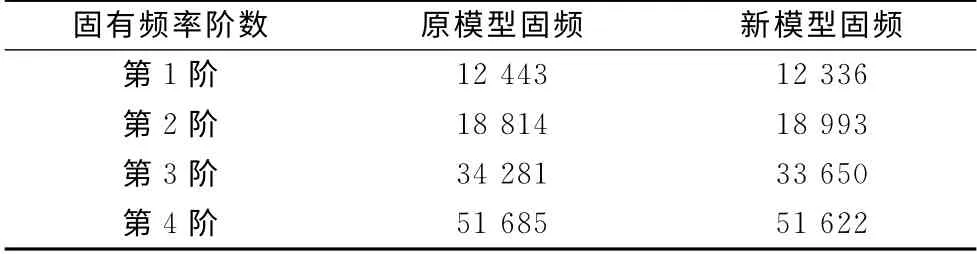
表2 优化前后的微加速度计固有频率对比Tab.2 Comparison of the natural frequencies of the initial and optimized micro－accelerometers Hz

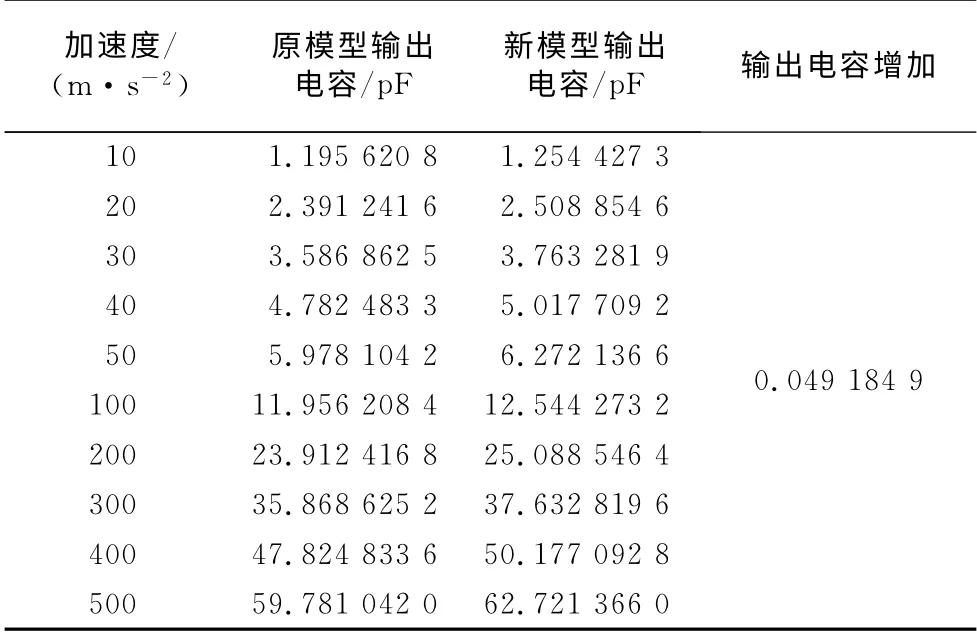
表3 优化前后的微加速度计输出电容对比Tab.3 Comparison of the output capacitance of the initial and optimized micro－accelerometers

由表2可见，微加速度计的前2阶固频差值为6 657Hz，比优化之前增加了286Hz，进一步避免了前2阶模态的耦合.由表3可见，微加速度计的电容输出性能提高了4.92%.由于输出电容与微加速度计的灵敏度呈正比关系，因而微加速度计的灵敏度也相应提高了4.92%.由于弹性梁的质量占微加速度计整体质量的比重约为1.4%，因而弹性梁结构的改变对品质因子（Q值）的影响可以忽略不计.

4 结论

（1）以MEMS 技术制备的电容式硅微加速度计为研究对象，建立了微加速度计最终的输出性能——检测电容的计算模型和计算方法，实现了面向微加速度计最终输出性能的动力学特性与检测特性的分析.在微加速度计的性能解析、结构优化等方面，采用所提出的模型和方法，可实现面向微加速度计最终输出性能的计算与分析.

（2）以提高微加速度计输出性能为目的，建立了微加速度计结构拓扑优化的流程、优化模型与目标函数.优化结果表明，优化后微加速度计的输出性能和灵敏度提高了4.92%；通过拓扑优化进一步限制了模态耦合，而微加速度计的品质因子却未受到影响.

［1］ 赵君辙，邢馨婷，杨中柳.线加速度计的现状与发展趋势综述［J］.计测技术，2007，27（5）：1.ZHAO Junzhe，XING Xinting，YANG Zhongliu.The summary of present situation and tendency of the linear accelerometer［J］.Metrology ＆Measurement Technology，2007，27（5）：1.

［2］ 任杰，樊尚春.硅基谐振式微机械加速度计的设计与仿真计算［J］.传感技术学报，2007，20（9）：1992.REN Jie，FAN Shangchun.Design and simulated calculation of Si－based micromechanical resonant accelerometer［J］.2007，20（9）：1992.

［3］ Coultate J K，Fox C H J，Mcwilliam S，et al.Application of optimal and robust design methods to a MEMS accelerometer［J］.Sensors and Actuators A：Physical，2008，142（1）：88.

［4］ Aaltonen L，Halonen K.Continuous－time interface for a micromachined capacitive accelerometer with NEA of 4μg and bandwidth of 300Hz［J］.Sensors and Actuators A：Physical，2009，154（1）：46.

［5］ Albarbar A，Badri A，Sinha J K，et al.Performance evaluation of MEMS accelerometers［J］.Measurement，2009，42（5）：790.

［6］ 刘广军，王安麟，姜涛，等.微机械陀螺结构形状自组织优化方法［J］.机械工程学报，2007，43（7）：99.LIU Guangjun， WANG Anlin，JIANG Tao，et al.Selforganizing optimization method of structural shape of micromachined gyroscope［J］.Chinese Journal of Mechanical Engineering，2007，43（7）：99.

［7］ Diaz A， Sigmund O. Checkerboard patterns in layout optimization［J］.Structure Optimization，1995，10（1）：40.

［8］ 李兆坤，张宪民.多输入多输出柔顺机构几何非线性拓扑优化［J］.机械工程学报，2009，45（1）：180.LI Zhaokun，ZHANG Xianmin. Topology optimization of multiple inputs and outputs compliant mechanisms with geometrically nonlinearity ［J］. Journal of Mechanical Engineering，2009，45（1）：180.

［9］ 张宪民，陈永健.考虑输出耦合时柔顺机构拓扑与压电驱动单元的优化设计［J］.机械工程学报，2005，41（8）：69.ZHANG Xianmin，CHEN Yongjian.Topology and actuation elements optimization of compliant mechanisms with output coupling terms control［J］.Chinese Journal of Mechanical Engineering，2005，41（8）：69.

［10］ 范文杰，范子杰，苏瑞意.汽车车架结构多目标拓扑优化方法研究［J］.中国机械工程，2008，19（12）：1505.FAN Wenjie，FAN Zijie，SU Ruiyi.Research on multiobjective topology optimization on bus chassis frame［J］.China Mechanical Engineering，2008，19（12）：1505.

［11］ 何建军，姜节胜.具有位移和频率约束的连续体结构拓扑优化的一种混合方法［J］.机械强度，2008，30（6）：941.HE Jianjun，JIANG Jiesheng.Hybrid method of topology optimization for continuum structures based on displacement and frequency constraints［J］.Journal of Mechanical Strength，2008，30（6）：941.