高架钢弹簧浮置板轨道减振特性分析

韦红亮，练松良，周 宇

（同济大学 道路与交通工程教育部重点实验室，上海201804）

高架轨道交通贯穿城市闹市区，带来的环境问题以振动噪声尤为突出.浮置板以减少由轨道传递到高架桥结构的振动能量为目的，降低了城市高架轨道交通的振动和二次噪声水平，在国内外城市轨道交通建设中得到广泛采用［1］.国内外针对浮置板轨道结构减振降噪的研究主要有理论解析法、数值计算法和室验测试法等3个方面.Cui F［2］，Hussein M F M［3］和Gupta S［4］等分别建立了浮置板轨道结构的理论解析模型，分析了浮置板轨道结构的隔振性能，以及相对位移激励下轮轨间动载荷和传递给基础的力；刘维宁［5］、耿传智［6］等分别建立了钢弹簧浮置板有限元模型，对浮置板轨道进行动力特性分析，分析了其传导比特性；Kawaharazuka T［7］和Cox S J等［8］分别通过比例模型对浮置板轨道结构的减振特性进行了分析，Hui C K［9］通过现场实验对浮置板轨道在63～200 Hz范围内的减振效果进行了测试，但以上文献未针对浮置板轨道对高架桥的减振特性进行理论分析.

在高架浮置板轨道结构减振设计中，减振器的刚度值和分布间距是影响减振效果的主要因素之一.本文采用有限元方法首先对浮置板轨道结构自振特性进行了分析，然后从时、频域角度分析了减振器刚度及分布间距变化对高架箱梁结构振动响应的影响，并结合现场测试对高架浮置板轨道结构的减振特性进行了分析，可为城市轨道交通的减振降噪设计提供参考依据.

1 计算模型

1.1 有限元振动计算理论

使用有限元方法进行结构振动计算，可以得到在移动荷载作用下结构随时间变化的节点位移、速度和加速度的响应，基本方程为

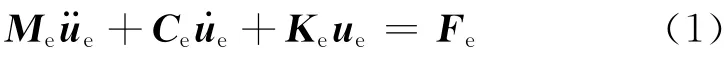
式中：Me，Ce和Ke分别为结构质量矩阵、阻尼矩阵和刚度矩 阵和ue分别为结构振动加速度、速度和位移；Fe为荷载向量.对于上述微分方程的求解可采用Nemark方法进行求解.

1.2 计算模型及参数

高架桥为25m 跨混凝土简支梁，截面形式为单箱单室箱梁，有限元模型如图1a所示，计算模型的物理参数如表1所示，箱梁结构截面等效尺寸如表2所示.钢轨为CHN60型，采用3维2节点梁单元进行模拟，网格最大尺寸为0.1 m；扣件为弹条II型，采用3维弹簧阻尼单元进行模拟，网格最大尺寸为0.05m；浮置板采用3维8节点实体单元进行模拟，网格最大尺寸为0.083m；箱梁结构采用3维4节点壳单元进行模拟，网格最大尺寸为0.2m.在1／2梁跨断面上，分别在钢轨、浮置板、轨道中心线、翼缘、腹板和梁底设置拾取点，拾取列车经过时的加速度信号，如图1b所示.

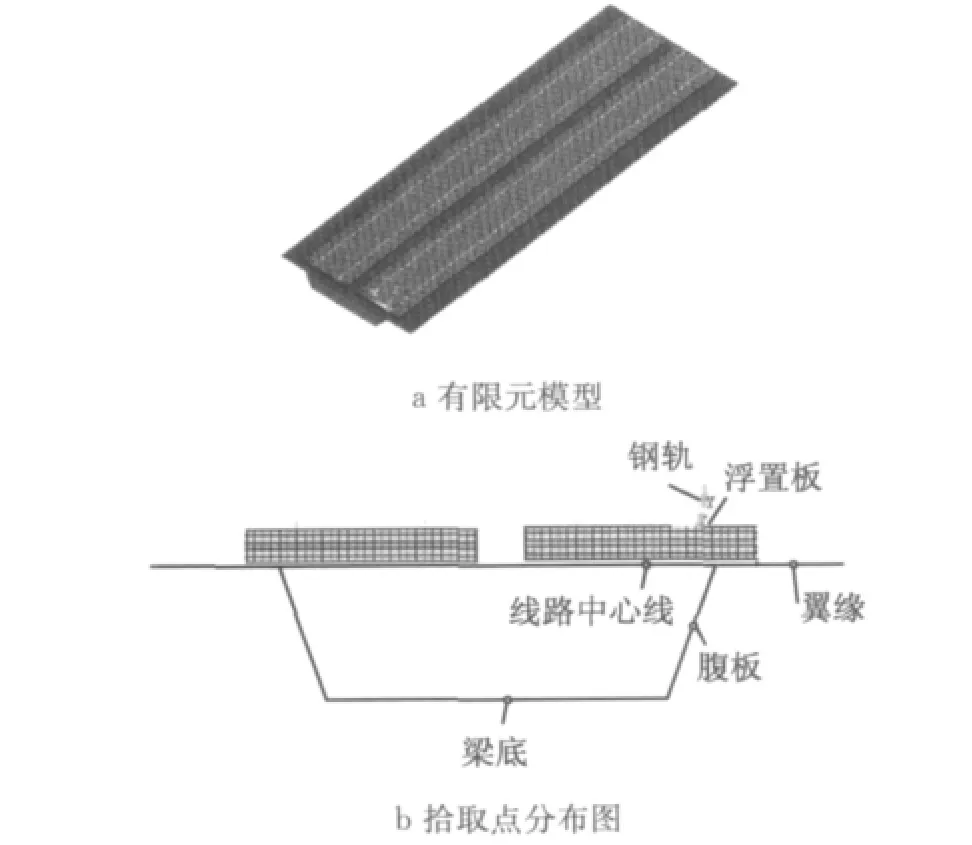
图1 有限元模型与拾取点分布Fig.1 FEM model and the selected points for analysis

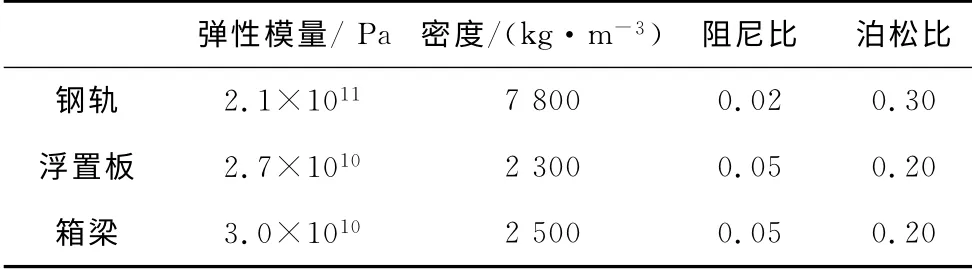
表1 有限元模型参数Tab.1 Parameters of FEM mode

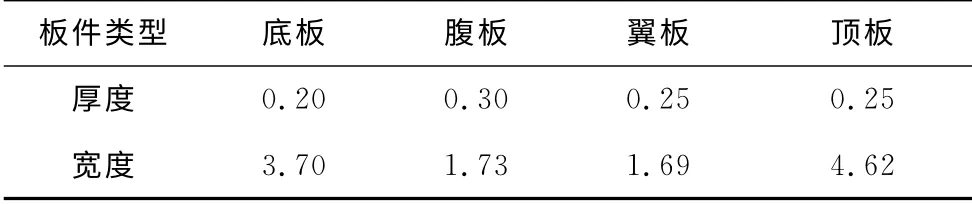
表2 高架桥截面板件等效尺寸Tab.2 Equivalent size of plate section in viaductsm

2 模态分析

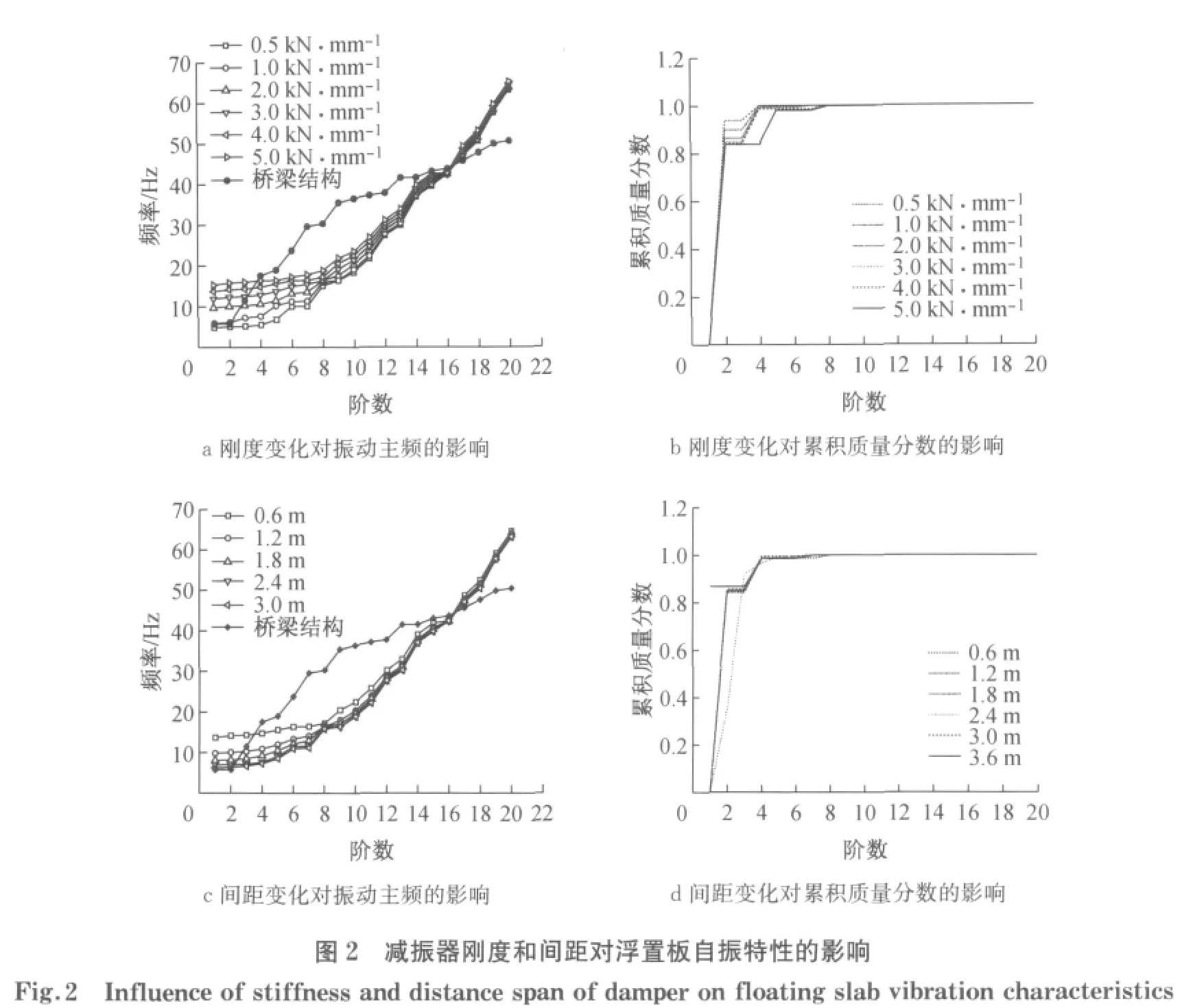
分别改变减振器刚度及间距，采用子空间迭代法对浮置板轨道结构和桥梁结构进行模态分析，提取前20阶振动频率和累积质量分数如图2所示.

图2表明，减振器刚度和间距的改变对浮置板前10阶自振频率影响较为明显，相同阶数下的自振频率随减振器刚度的减小而减小，随着减振器间距的增大而减小.当阶数为2时，浮置板的振动累积质量分数已达0.8；阶数为10时，累积质量分数接近于1，说明浮置板的振动能量以前10阶为主，减振器刚度减小时，前10阶的累积质量分数也稍有减小，减振器间距的改变对累积质量分数的分布特性几乎没有影响.

3 减振分析

采用SIMPACK 软件建立车辆轨道耦合模型计算出轮轨垂向接触力，然后输入到有限元模型中进行瞬态分析，阻尼分别为α＝0.2，β＝0.000 2，计算步长为10－3s，分别从时域和频域角度分析减振器刚度和间距变化对高架钢弹簧浮置板减振特性的影响.车辆类型为地铁A 型车，编组为单节动车，轨道不平顺为采用美国5级不平顺谱［10］，车速为80km·h－1.

3.1 时域分析

列车经过时，在减振器刚度为4.0kN·mm－1、间距为0.6m 的条件下，各拾取点的振动加速度时程曲线如图3所示，减振器刚度和间距变化时各拾取点的振动响应幅值如表3和表4所示.

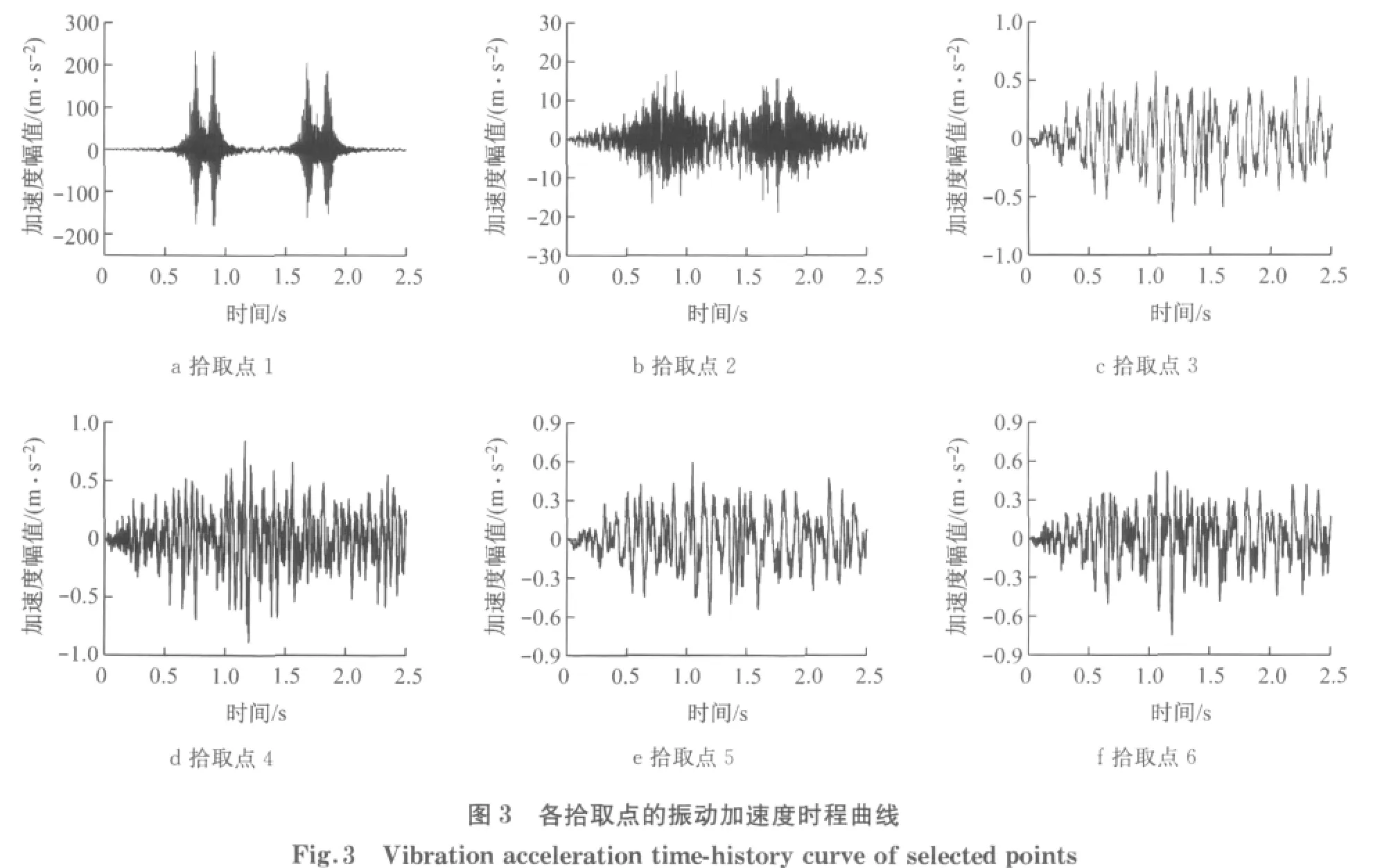
由图3、表3和表4可以得出如下结论：

（1）列车经过时，钢轨和浮置板的加速度时程具有较明显的因轮轨冲击作用而产生波形起伏，因减振器的作用，桥面板、翼缘、腹板和梁底的加速度时程已不存在明显的轮轨冲击；列车荷载作用下，钢轨、浮置板、桥面板、翼缘、腹板和梁底的加速度幅值在浮置板顶升前分别为237.4，5.58，3.69，6.15，5.13和2.54m·s－2，在浮置板顶升后钢轨和浮置板的加速度幅值分别为230～250m·s－2和15～30m·s－2，桥面板、腹板和梁底的振动加速度幅值均小于1m·s－2，说明浮置板轨道通过增大自身的振动幅值来达到降低高架桥振动幅值的目的.

（2）浮置板的加速度和位移幅值随减振器刚度的增大而减小，随减振器间距的增大而增大；箱梁结构各拾取点的振动加速度幅值随刚度的减小而减小，随间距的增大而减小，而位移受减振器刚度和间距变化的影响较小.

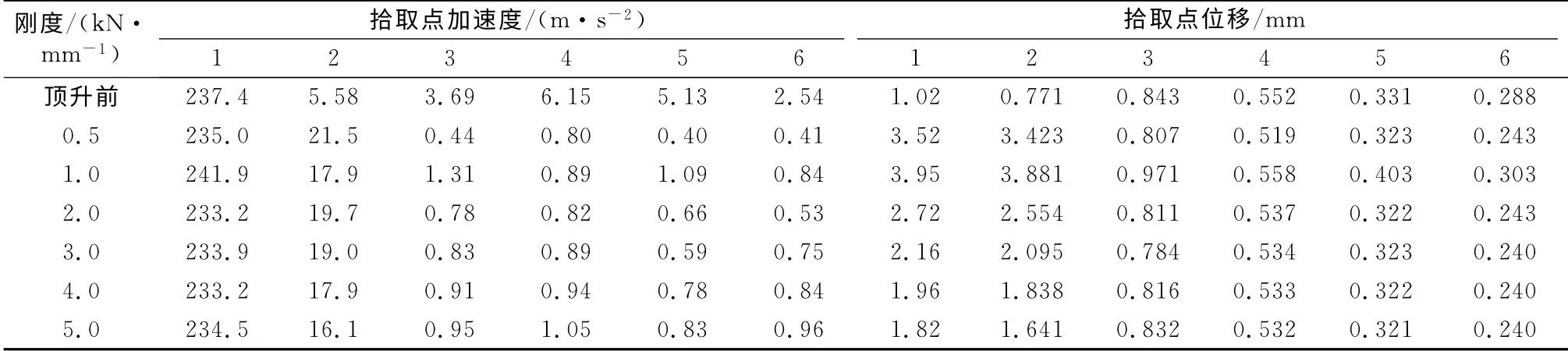
表3 间距为0.6m 时，减振器刚度变化对振动响应幅值影响Tab.3 Influence of stiffness of damper on vibration acceleration amplitude with span of 0.6m

表4 刚度为4kN·mm－1时，减振器间距变化对振动响应幅值影响Tab.4 Influence of span of damper on vibration acceleration amplitude with stiffness of 4kN·mm－1

3.2 频域分析

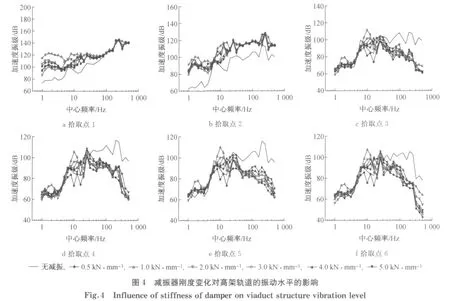
对各拾取点的振动时程进行1／3 倍频程分析，以分析减振器刚度和间距变化对轨道和高架桥结构振动水平分布的影响，结果如图4和图5所示.采用振动加速度级Lva对振动水平进行评价，计算方法如下式：

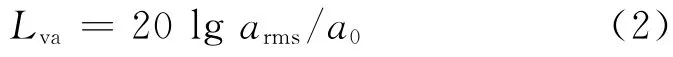
式中：Lva为振动加速度级，dB；arms为1／3 倍频程中心频率对应的振动加速度有效值，m·s－2；a0为基准加速度，取10－6m·s－2.

由图4可以得出以下结论：

（1）在小于80 Hz的频率范围内，浮置板顶升后钢轨振动水平出现增大的现象，增大值随减振器刚度的增加而减小.在8～200Hz范围内，浮置板的振动水平在顶升前后出现16～28dB的增大；在8～40Hz范围内，浮置板振动水平基本上随减振器刚度的减小而增大，从频域角度说明了浮置板轨道以增大自身的振动水平来达到减小对高架桥振动能量输入的目的；在40～200 Hz范围内，减振器刚度的变化对浮置板振动水平的影响较小.

（2）在8～25Hz范围内，浮置板顶升后箱梁结构各拾取点的振动水平基本上出现增大的现象，增大值约为8～18dB，主要是由于浮置板振动经过钢弹簧的传递所引起；在25～200 Hz范围内，箱梁结构各拾取点的振动水平在浮置板顶升后发生急剧减小，减小值最大可以达35dB，减振效果随减振器刚度的减小而增大.

（3）刚度为1.0kN·mm－1时，箱梁结构各拾取点在6.3～16Hz范围内振动水平发生增大现象，增大值最大可达到28.6dB，较减振器刚度取其他值时要大，说明当浮置板的自振频率与桥梁自振频率相一致时，浮置板轨道虽具备一定的减振效果，但减振能力发生一定程度的减弱.

由图5可以得出以下结论：

（1）在6.3～200 Hz范围内，减振器间距为0.6，1.2，1.8，2.4和3.0 m 时，浮置板的振动水平较浮置板顶升前分别高出11.5，14.3，17.5，20.5和22.2dB，说明浮置板的振动水平随减振器间距增大而增大，主要是由于减振器间距的增大导致单位长度浮置板的刚度降低所致.

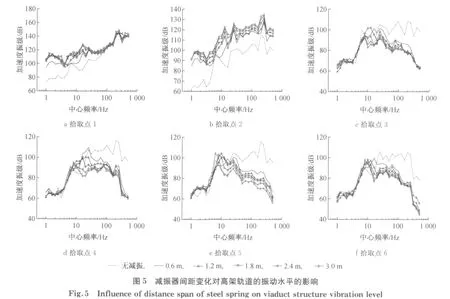
（2）在1～5 Hz的范围内，减振器间距变化对桥面板、翼缘、腹板和梁底的振动水平影响不大；当减振器间距分别为0.6，1.2，1.8，2.4和3.0m 时，箱梁结构各拾取点的振动水平在10～25 Hz，8～20 Hz，6.3～16Hz，6.3～12Hz和6.3～10Hz频率范围内较浮置板顶升前基本上出现增大的现象，增大值约为4～18dB；在25～100 Hz范围内，箱梁结构各拾取点的振动水平较浮置板顶升前出现减小的现象，减小值随减振器间距的增大而增大，箱梁顶板、翼缘、腹板和底板的振动水平减小值分别为11～22 dB，12～20dB，20～30dB和12～21dB.

4 现场实验分析

试验地点位于上海轨道交通某区段内，该区段线路为直线，轨道结构设有支承块和浮置板轨道结构，钢轨类型为CHN60，扣件类型为弹条II型，高架桥为单箱单室简支梁，跨度为30 m，列车运行速度为55km·h－1.分别在1／2梁跨断面上钢轨、轨道板和桥面板上布置传感器，拾取列车经过时各测点的垂向加速度信号，采样频率为5 000Hz.对测试波形数据进行时频统计分析，结果如表5和图6所示.

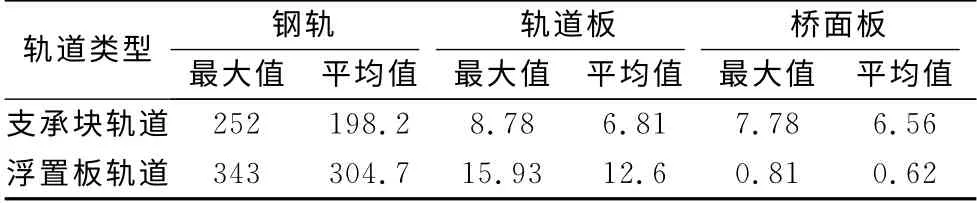
表5 实测加速度幅值统计表Tab.5 Amplitude statistics of vibration acceleration by field test m·s－2

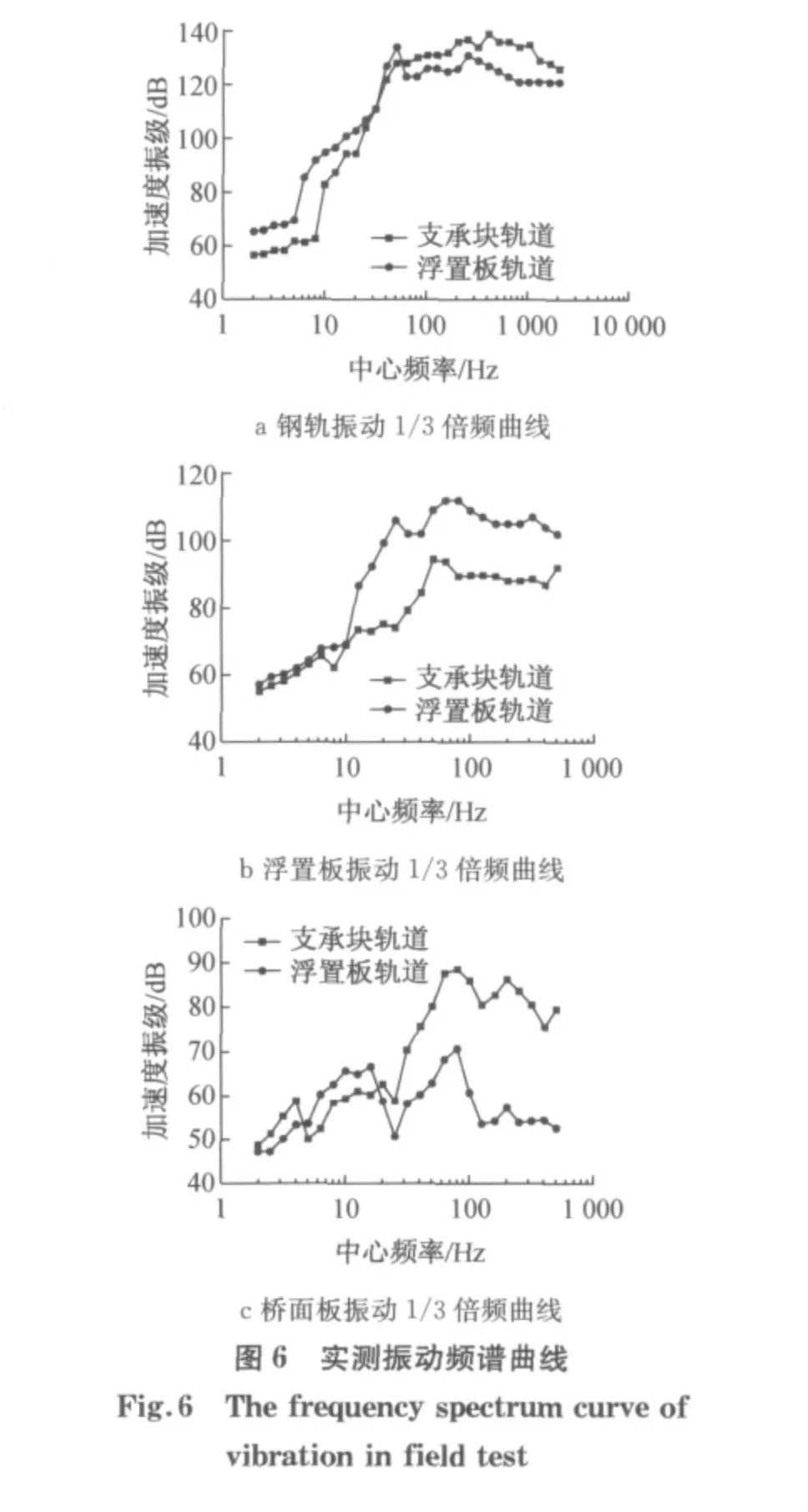
图6和表5表明：

（1）列车荷载作用下，支承块轨道钢轨、承轨台和桥面板加速度幅值的最大值和平均值分别为252，8.78，7.78m·s－2和198.2，6.81，6.56m·s－2，而浮置板轨道钢轨、轨道板和桥面板加速度幅值最大值和 平 均 值 分 别 为343，15.93，0.81 m·s－2和304.7，12.6，0.62m·s－2，从时域角度上说明浮置板轨道具有良好的减振效果.

（2）两种轨道结构的钢轨振动频率主要分布在300～1 000Hz范围内；承轨台和浮置板的振动频率主要分布在63～100Hz和12.5～80Hz范围内，主要是因为浮置板参振质量的增大和刚度的降低导致振动频率出现降低；由于承轨台和桥梁之间采用刚性连接，桥面板振动频率分布特性与承轨台一致；浮置板轨道在轨道板与桥面板之间通过钢弹簧连接，因此桥面板的振动频率主要分布在6～16 Hz和50～80Hz范围内，6～16 Hz的低频振动主要因浮置板的自振引起，50～80 Hz的中频振动主要由浮置板的振动通过钢弹簧向桥面传递所致.

（3）在63～2 000 Hz范围内，浮置板钢轨的振动水平较支承块轨道钢轨低12dB，说明浮置板轨道对轮轨噪声具有一定的降噪效果；浮置板在10～500 Hz的振动水平内较承轨台平均高出18.2dB，两者最大差值可达31.4dB，而浮置板轨道桥面板的振动水平在25～500 Hz范围内较支承块轨道平均低25.4dB，说明浮置板轨道以增大自身的振动来达到减小对桥梁结构振动能量输入的目的.

5 结论

（1）模态分析表明，减振器刚度和间距的改变对浮置板前10阶自振频率影响较为明显，相同阶数下自振频率随减振器刚度的减小而减小，随着减振器间距的增大而减小，浮置板的振动能量以前10阶为主，减振器间距的改变对累积质量分数分布特性几乎没有影响.

（2）相同条件下，浮置板的加速度和位移幅值随减振器刚度的增大而减小，随减振器间距的增大而增大，高架桥结构的振动加速度幅值随刚度的减小而减小，随间距的增大而减小，高架桥结构的位移受减振器刚度和间距变化的影响较小.

（3）浮置板轨道以增大自身的振动水平以减小对高架桥振动能量输入，减振器刚度和间距的变化都是通过改变浮置板单位长度支承刚度来达到控制减振效果的目的；浮置板顶升后，浮置板的振动水平在8～200Hz范围内可以增大16～28dB，高架箱梁结构顶板、翼缘、腹板和梁底的振动水平在25～100 Hz范围内分别减小11～22dB，12～20dB，20～30 dB和12～21dB，减小值随减振器刚度的增大而减小，随减振器间距的增大而增大.

（4）现场实测分析表明，浮置板轨道钢轨振动频率主要分布在300～1 000 Hz范围内，浮置板的振动频率主要分布在12.5～80.0 Hz范围内，桥面板的振动频率主要分布在6～16 Hz和50～80 Hz范围内；浮置板轨道对在63～2 000Hz的轮轨噪声具有一定的降噪效果，可达12dB；相对支承块轨道而言，在25～500Hz范围内浮置板轨道对高架箱梁结构减振效果可达25.4dB.

［1］ Nelson J T.Recent developments in ground－borne noise and vibration control［J］.Journal of Sound and Vibration，1996，193（1）：367.

［2］ Cui F，Chew C H.The effectiveness of floating slab track system—part I：receptance methods［J］.Applied Acoustics，2000，61：441.

［3］ Hussein M F M ，Hunt H E M.Modeling of floating－slab tracks with continuous slabs under oscillating moving loads［J］.Journal of Sound and Vibration，2006，297（1－2）：37.

［4］ Gupta S， Degrande G. Modeling of continuous and discontinuous floating slab tracks in a tunnel using aperiodic approach［J］.Journal of Sound and Vibration，2010，329：1101.

［5］ 丁德云，刘维宁，李克飞，等.钢弹簧浮置板轨道参数研究［J］.中国铁道科学，2011，32（1）：30.DING Deyun，LIU Weining，LI Kefei1，et al.Parametric study of the steel spring floating slab track［J］.China Railway Science，2011，32（1）：30.

［6］ 耿传智，楼梦麟.浮置板轨道结构系统振动模态分析［J］.同济大学学报：自然科学版，2006，34（9）：1201.GENG Chuanzhi，LOU Menglin.Vibration model analysis of floating slab track system ［J］.Journal of Tongji University：Natural Science，2006，34（9）：1201.

［7］ Kawaharazuka T， Hiramatsu T， Ohkawa H， et al.Experimental study on vibration reduction by isolated railway［C］∥The 1996 International Congress on Noise Control Engineering，Liverpool：Institute of Acoustics（Great Britain），1996：1549.

［8］ Cox S J，Wang A，Morison C，et al.A test rig to investigate slab track structures for controlling ground vibration ［J］.Journal of Sound and Vibration，2006，293（3－5）：901.

［9］ Hui C K，Ng C F.The effects of floating slab bending resonances on the vibration isolation of rail viaduct ［J］.Applied Acoustics，2009，70：830.

［10］ 雷晓燕.轨道力学与工程新方法［M］.北京：中国铁道出版社，2002.LEI Xiaoyan.New methods in railroad track mechanics and technology［M］.Beijing：China Railway Publishing House，2002.