交通网络需求脆弱性分析及应用

杨 超，涂颖菲，陈小鸿

（同济大学 道路与交通工程教育部重点实验室，上海201804）

Nicholson和Dalziell指出，当出行路径不可用时，出行者行为可能有以下几种反应：取消出行、推迟出行、改变目的地、改变交通方式、更换路径［3］.若忽略交通需求的变化，会对交通网络所受到影响的估计产生一定偏差.需求脆弱性则是同时考虑交通网络的需求和供给两方面的变化，基于异常事件下交通系统供需平衡的变化程度来评价网络承受异常事件的能力.由于常规的四步骤交通需求预测方法存在问题，学者们开始研究其他交通需求预测模型，这些模型主要是组合或整合模型［4－10］.其 中Oppenheim 提出的交通需求组合模型CTDM（combined travel demand model）是一种基于随机效用理论的需求预测模型［8］，它组合了出行—分布—方式—路径4个层面.Chen等的研究表明若不同时考虑4个层面的行为，会高估在异常事件状况下整个交通系统所受到的影响［11］.

可达性是交通网络分析和城市规划中的一个基本概念，学者们给可达性赋予了多种具体的量化方法.在交通网络脆弱性的研究中，也有一些学者从可达性降低的角度来衡量交通网络所受到的影响［12－14］，然而大多数研究主要是基于可达性的变化来评价具体的异常事件所造成的影响.本文所提出的需求脆弱性则是要评价网络承受异常事件的能力，使得脆弱性分析能用于支持在规划与管理层面改善网络性能.因此需要将具体异常事件所造成的影响提升为网络层面的需求脆弱性指标，并讨论其在交通规划与管理中的应用.

1 需求脆弱性分析方法

1.1 需求组合模型

根据文献［8］的研究，假设每个出行者的决策过程有如下自上而下的结构：

（1）给定位置i处的1个人，1个给定的时间段（小时，天等），和1个活动（如购物、工作、娱乐等），1个潜在的出行者首先决定是否出行.Pt｜i是潜在出行者在研究时间段内出行的概率；

（2）给定第1层次中的选择，个体选择目的地j进行活动的条件概率为Pj｜i；

（3）给定前2 个决定的结果，个体选择方式m（从i到j的出行）进行活动的条件概率为Pm｜ij；

（4）给定前面所有决定的结果，个体选择路径r（从i到j采用方式m的出行）进行活动的条件概率为Pr｜ijm.

高校固定资产信息化管理，必须执行责任到人的要求，固定资产的申购、登记入库及验收、变动处置等每个环节都明确负责人，全程透明化管理、规范性操作。通过固定资产管理平台，对固定资产从申购到销账整个生命周期进行动态管理，可以有效避免固定资产的流失，保障固定资产的安全有效。

根据随机效用理论，每个阶段行为的概率都用多元罗吉特选择函数来进行计算，如：在第1 阶段（也就是决定是否出行）从起点i出发的出行数Ti，通过条件概率Pt｜i乘以起点i处潜在的出行者数量Ni来得到.条件概率Pt｜i通过下式计算：

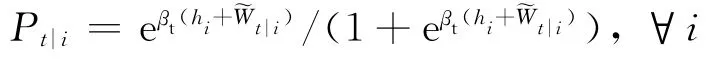
式中：βt 是与出行选择相关的参数；hi是起点i的吸引力；~Wt｜i是期望获得的效用，它取决于下个阶段（目的地选择阶段）的效用，即

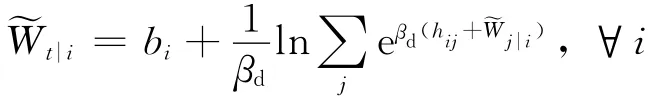
式中：bi是个体选择从起点i出行的预算；βd 是与目的地选择相关的参数；hij是从i到j出行的吸引力.在目的地阶段选择的期望效用也取决于方式选择阶段的效用，以此类推，直到路径选择阶段.所以，起点i处的个体采用方式m经过路径r到达目的地j的概率可以通过将“分层”结构中从路径选择到出行决定过程中每个阶段的条件概率相乘而得到，即

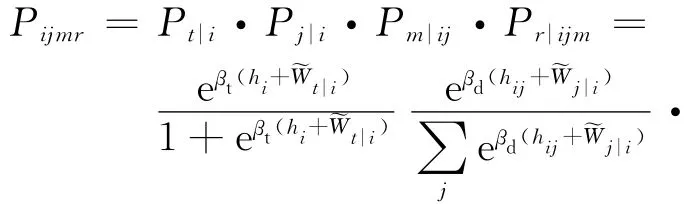
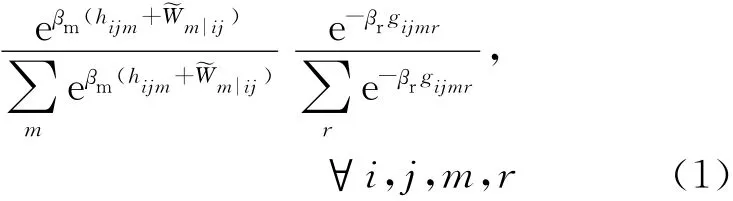
式中：βr，βm，βd，βt 分别是与路径、方式、目的地和出行选择相关的参数；hijm是i和j之间方式m的吸引力；gijmr为起点i和终点j之间方式m的路径r的广义成本为路段a上方式m的广义路段出行成本函数为路段—路径关联系数.

采用将出行者视作城市出行的消费者这一概念，路径需求可以通过求解满足预算和守恒约束的直接效用的最大化问题得到.Oppenheim 证明了该最优化问题的Karush－Kuhn－Tucker（KKT）条件，分别给出选择路径（Pr｜ijm）、方式（Pm｜ij）、目的地（Pj｜i）和是否出行（Pt｜i）的概率，如等式（1）所示，并证明了解的存在性和惟一性［8］.蒲琪等给出了一种求解该模型的算法［15］.

1.2 需求脆弱性指标

需求脆弱性指标用于定量评价网络承受某类异常事件的能力，该能力越强，则意味着异常事件的发生对交通网络上供需平衡关系的影响越小；反之，网络越脆弱，则意味着在异常事件下，网络供需平衡关系的变化越大.因此，需求脆弱性指标的核心是定量描述供需平衡关系，本文选取Ben－Akiva和Lerman所给出的基于效用的可达性指标［16］来对其进行描述

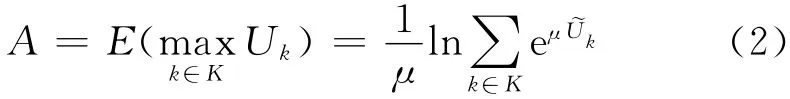
式中：K为选择集；Uk为选择k所获得的随机效用；μ为调整参数.

Chen等［11］在研究中根据求解CTDM 得到期望获得的效用指标，给出了每个层面的可达性指标，并且指出异常事件下该指标变化越小则表示网络、小区、OD（origin－destination）对或交通方式受到的影响越小.为了将具体异常事件的影响转化为网络承受异常事件能力，本文将需求脆弱性指标VDVI定义为：在一定需求水平下，交通网络上发生某类异常事件的所有情况下各个层面可达性指标的变化的平均值.根据应用目标，可以对不同层面进行需求脆弱性分析

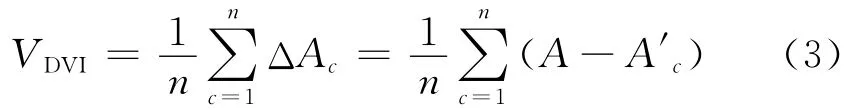
式中：n为某类异常事件所有可能发生的情况的数量；A，A′c分别为正常情况下和异常事件发生时可达性指标.

2 需求脆弱性分析实例

2.1 路网描述

本节以图1 中所示的网络为对象，网络包括6个节点、8条路段，2个OD 对1 4和1 6.该交通网络系统中包括两种交通方式：小汽车和公交，且使用同样的网络拓扑结构.各路段在自由流条件下的行程时间以及通行能力如表1所示，下标c和t分别对应于小汽车和公交方式.

图1 需求脆弱性分析示例网络Fig.1 Trial network for demand vulnerability analysis

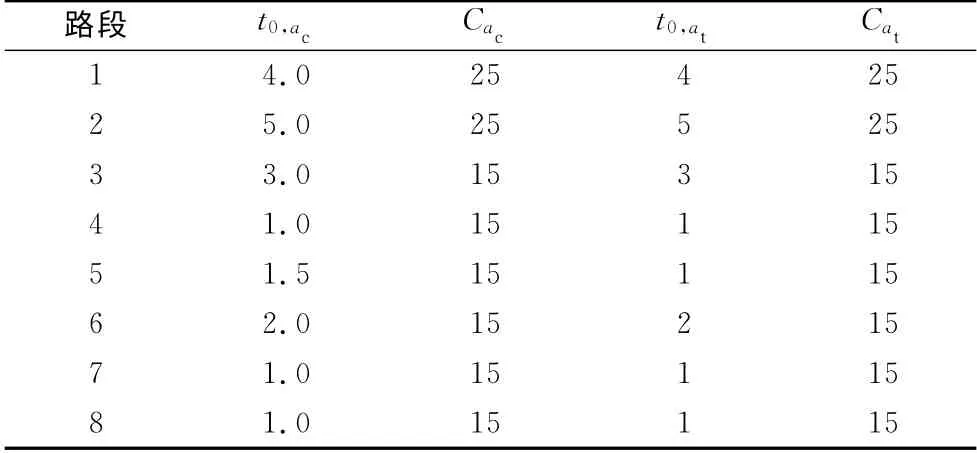
表1 示例路网路段数据Tab.1 Link data for trial network

路段成本函数分别为

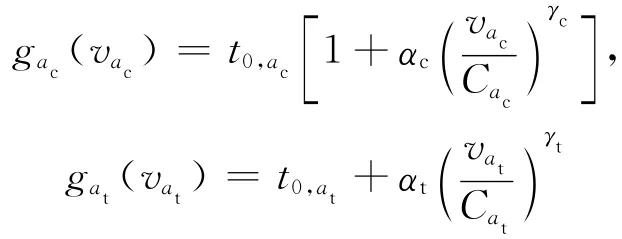
式中：vac和vat分别为小汽车和公交的路段流量；t0，ac和t0，at分别是小汽车和公交的自由流条件下的行程时间；Cac和Cat分别是小汽车和公交的路段通行能力；对于小汽车，αc和γc分别设为0.15和4.00；对于公交方式αt和γt分别设为0.06和2.00.

小区1 的人口N1和吸引力h1分别为200 和5.0.其他吸引力参数：h14和h16分别为2.0 和3.0；h14c，h14t，h16c，h16t分别为1.5，1.6，1.8，1.4；参数βr，βm，βd，βt 分别为2.0，1.0，0.5，0.2.

2.2 需求脆弱性指标计算

基于对需求组合模型CTDM 的求解，进行各层面的可达性指标的计算，可以得到异常事件在出行需求的各个层面所产生的影响的程度.

以路段小汽车和公交的通行能力显著降低的异常事件为例（为保证模型的正常计算，设置通行能力降低到1）.每条路段分别发生异常事件情况下各层面脆弱性指标如表2所示.可以看到网络层面的脆弱性小于小区层面，这是因为有一部分需求取消了出行，使得网络供需平衡的问题得到缓解.而小区的脆弱性则在两个OD 对之间，同样OD 对层面的脆弱性也在两种交通方式之间.脆弱性指标呈现出从方式选择层面传递到网络层面逐渐减小的趋势，这也说明了出行者行为选择的空间越大，网络承受异常事件的能力也越好.也再次说明需求组合模型考虑了出行者各阶段的行为选择，能更准确地反映异常事件下网络的供需关系.

表2 各层面脆弱性指标Tab.2 VDVIon different levels

2.3 降低需求脆弱性的方案比较

2.3.1 需求总量控制与交通管理手段

需求脆弱性分析方法可以用于对控制小区人口、调整目的地吸引力（如减少停车位）、调整交通方式吸引力（如降低公交票价）以及调整路径选择参数（如发布交通诱导信息）等措施的效果进行评价.以下仍以一条路段上的小汽车和公交通行能力同时显著降低的异常事件为例进行讨论.

各管理手段下降低网络脆弱性效果如表3.可以发现：网络正常状态下的可达性好，承受异常事件的能力并不一定强.同时，横向比较需求总量控制以及各种交通管理措施的效果发现：需求总量控制对降低需求脆弱性的效果是最显著的；其次是调整路径选择参数，调整目的地和公交方式的吸引力后脆弱性指标的变化不明显.

2.3.2 提高路网供给水平

同样在需求为200，1条路段2种交通方式的通行能力均显著降低的异常事件情况下，分别比较3种提高路段通行能力20%的方案的效果（见表4）.3种方案可达性和脆弱性指标的对比显示：网络正常状态下的可达性好并非意味着承受异常事件的能力强；提高路段公交的通行能力对于降低网络的需求脆弱性效果比提高小汽车通行能力更好，甚至对于有些路段效果好于同时提高小汽车和公交的通行能力（如路段1，2，4，8）；而只提高路段小汽车的通行能力对于降低需求脆弱性的效果并不好.

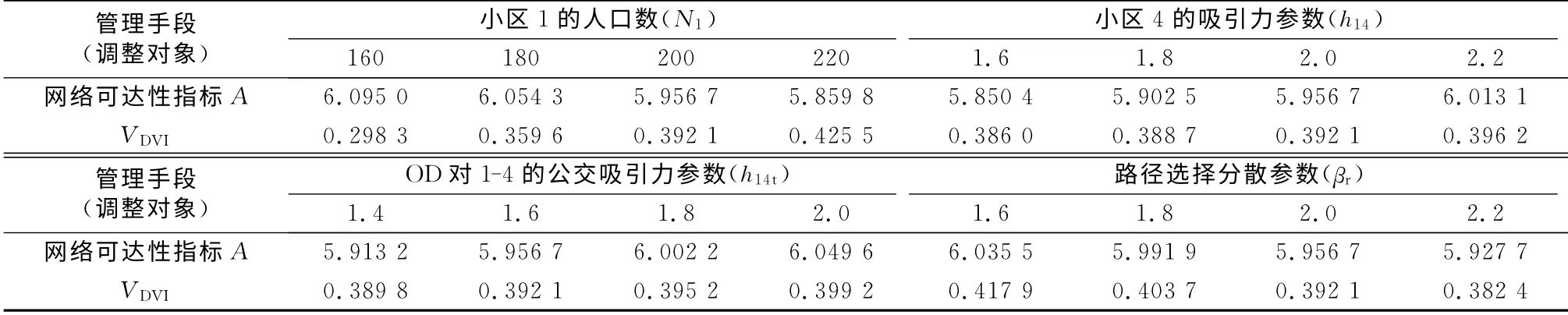
表3 不同管理手段下网络层面VDVITab.3 VDVI with different management measures

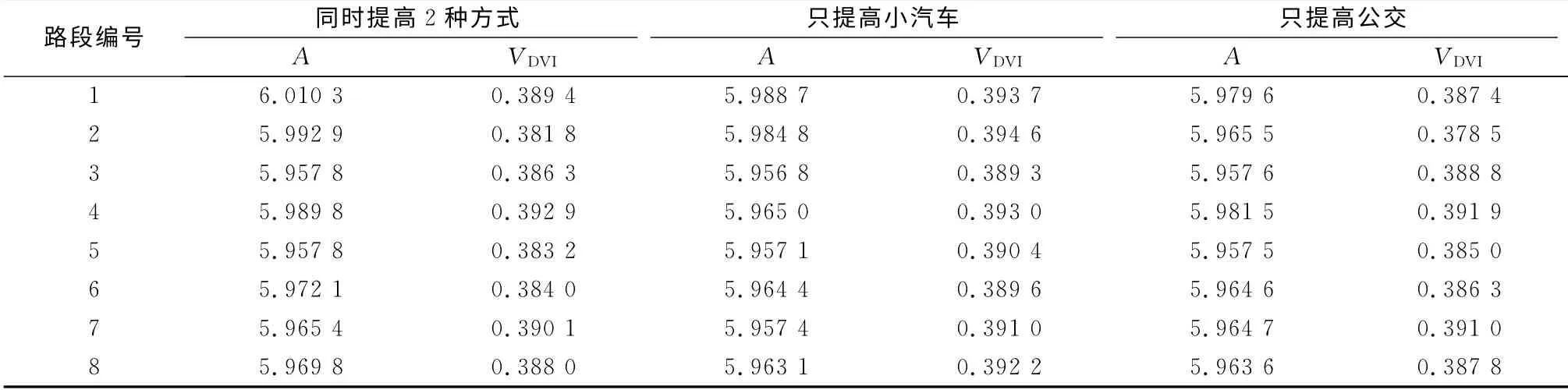
表4 提高通行能力20%时VDVITab.4 VDVIafter augment of capacity by 20%

3 结论

为了考虑在交通网络供给条件发生变化时交通需求随之所发生的变化，本文采用基于随机效用理论的交通需求组合模型和可达性指标作为交通网络需求脆弱性分析的基础.已有研究更偏重于对具体异常事件的影响评价，而本文提出的需求脆弱性指标反映的是在一定需求水平下，交通网络各层面承受某类异常事件的能力，使其能够运用于规划与管理层面改善网络性能.

分析发现，正常状况下网络可达性好，承受异常事件的能力并不一定强.示例网络的计算结果表明：小区人口越少，网络可达性越好，且脆弱性越低；降低目的地吸引力后虽然网络层面可达性降低，但承受异常事件的能力增加；提高公交的吸引力后虽然网络层面可达性提高，但承受异常事件的能力降低；路径选择参数值越大，网络层面的可达性降低，但承受异常事件的能力增加.此外，提高路段公交的通行能力对于降低网络的需求脆弱性效果比提高小汽车通行能力更好，甚至对于有些路段效果好于同时提高小汽车和公交的通行能力，并且提高路段通行能力对于提高网络正常状态下可达性效果最好的路段，并非能同时也提高网络承受异常事件的能力.

因此，基于交通网络需求脆弱性分析，一方面可以定量评价网络承受异常事件的能力，另一方面可以应用于交通规划与管理中，为决策者提供交通需求管理以及道路通行能力改善的决策依据，使得网络在异常事件发生时供需平衡所发生的变化更小，即承受异常事件的能力更强.

［1］ 涂颖菲，杨超，陈小鸿.路网拓扑脆弱性及关键路段分析［J］.同济大学学报：自然科学版，2010，38（3）：364.TU Yingfei，YANG Chao，CHEN Xiaohong.Analysis of road network topology vulnerability and critical links［J］.Journal of Tongji University：Natural Science，2010，38（3）：364.

［2］ 陈冬栋.面向城市路网脆弱性的交通事件影响研究［D］.上海：同济大学交通运输工程学院，2011.CHEN Dongdong.Traffic incident impact study based on urban network vulnerability［D］.Shanghai：College of Transportation Engineering of Tongji University，2011.

［3］ Nicholson A，Dalziell E.Risk evaluation and management：a road network reliability study［C］／／The Network Reliability of Transport.Proceeding of the 1st International Symposium on Transportation Network Reliability （INSTR），New York：Pergamon，2003：45－59.

［4］ Bar－Gera H，Boyce D.Origin－based algorithms for combined travel forecasting models［J］.Transportation Research Part B.2003，37（5）：405.

［5］ Florian M，Wu J H，He S.A multi－class multi－mode variable demand network equilibrium model with hierarchical logit structures ［C］／／Transportation and Network Analysis：Current Trends.Dordrecht：Kluwer，2002：119－133.

［6］ Lam W H K，Huang H J.A combined trip distribution and assignment model for multiple user classes［J］.Transportation Research Part B.1992，26（4）：275.

［7］ Safwat K N A，Magnanti T L.A combined trip generation，trip distribution，mode split，and trip assignment model［J］.Transportation Science.1988，22（1）：14.

［8］ Oppenheim N.Urban travel demand modeling［M］.New York：John Wiley ＆Sons，Inc.，1995.

［9］ 喻翔，毛敏，刘建兵.城市交通需求预测组合模型的研究［J］.西南交通大学学报，2003，38（1）：75.YU Xiang，MAO Min，LIU Jianbing.Study on combined models of demand forecasting for urban traffic［J］.Journal of Southwest Jiaotong University.2003，38（1）：75.

［10］ 杜刚诚，彭国雄.交通组合模型在交通需求预测中的应用研究［J］.武汉理工大学学报：交通科学与工程版，2004，28（1）：92.DU Gangcheng，PENG Guoxiong.A study of application of combined model in traffic demand forecasting［J］.Journal of Wuhan University of Technology：Transportation Science ＆Engineering.2004，28（1）：92.

［11］ Chen A，Yang C，Kongsomsaksakul S，et al.Network－based accessibility measure for vulnerability analysis of degradable transportation networks［J］.Networks and Spatial Economics.2007，7（3）：241.

［12］ D’Este G M，Taylor M A P.Application of accessibility based methods for vulnerability analysis of strategic road network［J］.Networks and Spatial Economics.2006，6：267.

［13］ Lleras－Echeverri G，Sanchez－Silva M.Vulnerability analysis of highway networks，methodology and case study［J］.Proceedings of Institution of Civil Engineers：Transport.2001，147（4）：223.

［14］ Sohn J.Evaluating the significance of highway network links under the flood damage：an accessibility approach［J］.Transportation Research Part A.2006，40：491.

［15］ 蒲琪，杨超，涂颖菲.基于二次插值法的交通需求组合模型算法［J］.同济大学学报：自然科学版，2009，37（12）：1615.PU Qi，YANG Chao，TU Yingfei.A quadratic interpolation method－based algorithm for a combined travel demand model［J］.Journal of Tongji University：Natural Science.2009，37（12）：1615.

［16］ Ben－Akiva M，Lerman S R.Disaggregate travel and mobilitychoice models and measures of accessibility［C］／／Proceedings of the 3rd international conference on behavioural travel modeling.London：Croom－Helm，1979：654－679.