基于记忆多项式模型的数字预失真器FPGA实现

韩 非， 郭正琨， 吕海飞

（上海无线电设备研究所，上海200090）

0 引言

随着无线通信的飞速发展，通信频谱资源变得越来越紧张，导致各种具有高频谱利用率和宽频带通信体制的出现，如16QAM调制、OFDM调制等。但这些调制信号具有较高的峰均比（峰值平均功率比）［1］，对功放的线性度要求较高。当功放工作在饱和点附近时，信号会产生严重的带内失真和带外失真。带内失真使信号星座图发生扩散和偏转，造成误码率性能下降；带外失真使信号频谱扩展，对邻信道产生干扰。为解决功放效率和线性度之间的矛盾，提高通信系统性能，就必须采用功放线性化技术。常用的功放线性化技术有前馈法（feed forward）、反馈法（feedback）、用非线性器件实现线性化法（LINC）和预失真法（pre－distortion）［2］。由于预失真法便于与数字信号处理和自适应技术相结合，具有调试简单、适应性好、带宽高等特点，使得它在现代通信发展中扮演着越来越重要的角色。

当信号传输带宽较大时，功放记忆效应比较显著，传统无记忆预失真技术线性化效果将会严重恶化［3］。本文针对功放的记忆效应和硬件实现的复杂度，采用记忆多项式模型设计预失真器，并在FPGA实现上给予简化，便于向工程应用推广。

1 数字预失真基本原理

预失真技术通过在非线性功放前级联一个与其幅度和相位特性相反的预失真器，把输入信号预先往功放特性相反的方向失真，从而使功放的输入输出在整体上呈现线性关系［4］。其基本原理如图1所示。

图1 预失真系统原理框图

设系统的输入、输出信号为x（t）、y（t），预失真器和功放的传输特性函数分别为FPD（t）、FPA（t）。预失真线性化技术就是使输入信号预先经过预失真器再接入功放输出。设xpd（t）为预失真 器 输 出，则 xpd（t）＝ FPD［x（t）］，y（t）＝FPA［xpd（t）］，可得

当整个系统为理想线性的时候，输出信号应该为

式中：G为放大器理想线性输出的增益，为一个常数。

数字预失真在通信系统的基带或数字中频完成信号预失真，把低频的模拟信号转化为数字信号进行处理，其系统框图如图2所示。

图2 自适应数字预失真原理图

在实际工作环境中，功放特性会随环境温度、供电电压、器件老化、信道切换发生改变，导致通信系统性能下降。为保证预失真系统的稳定工作，要求预失真器的补偿特性具有随功放特性变化而自适应调节的能力。既能灵活的对功放线性化，又能较好的解决功放系统的稳定性问题，同时还要保证具有较高的非线性性能改善程度。随着自适应技术的应用发展，现在已有多种自适应算法成功应用于预失真器的自适应补偿中。

2 功放的记忆多项式模型

根据功放输入输出关系，精确模拟功放非线性是分析功放系统和设计预失真系统的关键一步。Volterra级数是模拟有记忆非线性行为的常用方法［5］，但是它迭代运算量大，实现复杂度高，在实际应用中，大多数的功放需要采用高阶Volterra级数预失真来校正其非线性，这使得该缺点更加突出，以致于变得不实用。

幂级数是分析非线性系统的通用工具，一般的功放特性可以由幂级数展开的形式来表示。在通常情况下，功放输出信号中只有奇次阶的互调分量才会落在基波信号频率附近，偶次阶的互调分量都落在远离基波的位置，可以用滤波器来消除，即带内失真主要是由奇次阶互调分量引起的［6］。奇次互调分量只能由奇次方项产生。则在功放多项式模型分析中可以把偶次方项去掉，从而简化模型。通过在多项式模型前增加一系列延迟单元来描述功放的记忆效应，从而构成记忆多项式模型。相比Volterra级数，它将功放的记忆效应和非线性分别处理，并去掉偶次项，使其结构和迭代算法都大为简化。其原理图如图3所示。

图3 记忆多项式模型结构框图

其表达式如下：

式中：x（n）和y（n）分别表示输入输出复包络信号；p为延迟单元的延迟数，即为记忆深度，一般来说p越大，记忆深度越深，记忆模型越精确，但系统也越复杂。

3 软件仿真结果及分析

用记忆多项式模型来进行功放辨识和预失真器设计的软件仿真，系统仿真方案如图4所示。

图4 软件仿真方案

首先对功放模型进行离线辨识，仿真中的功放具有Weiner特性，辨识的期望值是使在相同输入数据下，辨识模型的输出信号和Weiner功放的输出信号误差最小。得到功放辨识模型后，将其复制，用来进行离线预失真器的设计。使用两个与功放辨识模型相同结构的记忆非线性模型，一个位于反馈支路，以训练器命名，另一个复制训练所得的模型参数，以预失真器命名，完成预失真功能。训练器完成一次系数的更新，预失真器就复制一次。当二者的输出趋近相同时，即u′（k）＝u″（k），误差e′（k）＝0，它们的输入也将一致，有y（k）＝y′（k）＝x（k），从而实现线性化过程。

本文软件仿真中假设功放的线性增益为1，功放辨识模型和预失真器均采用记忆多项式结构。记忆多项式系数更新采用NLMS算法，取抽头延时为3，多项式阶数为5，训练序列取4 096个16 QAM调制的OFDM信号点。仿真结果如图5、图6所示。

图5 预失真前后信号频谱特性比较

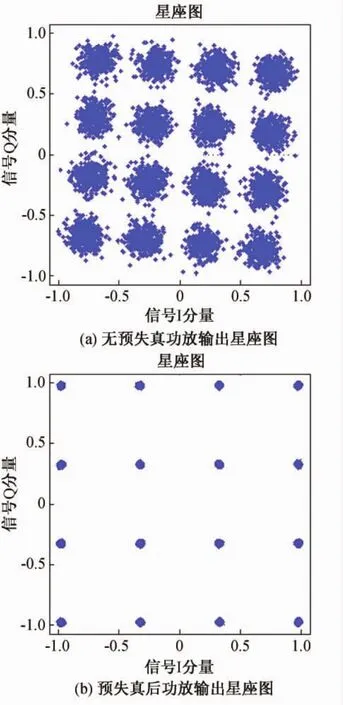
图6 预失真前后功放输出星座图比较

预失真后输出信号频谱扩展得到有效抑制，邻道干扰改善约21 d B；预失真后信号星座图的幅度和相位失真都得到了补偿。可见该方案设计的预失真器可以有效消除功放的非线性和记忆效应，极大程度的改善系统通信性能。

4 硬件实现及测试结果分析

考虑到系统实现的复杂性及FPGA实现的难度，采用阶数为5、延时为3的记忆多项式，并展开如下：

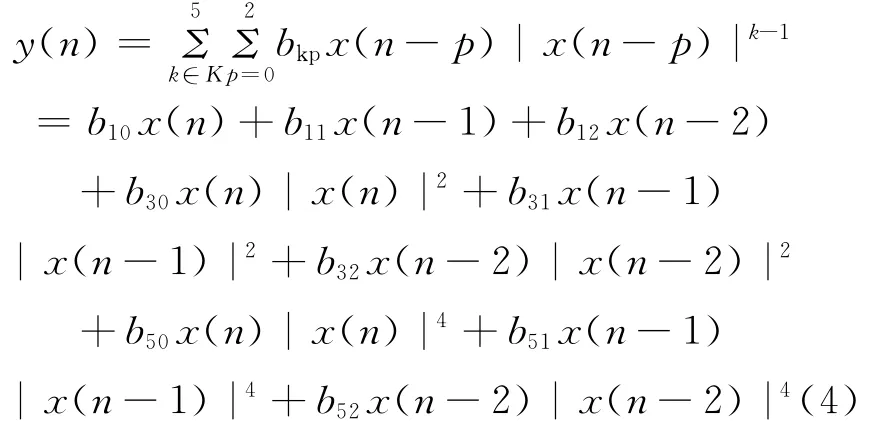
式中：x（n）和y（n）分别为系统在采样时刻n时的输入和输出；bkp为记忆多项式系数。为了算法上描述方便，采用下面的矩阵形式进行表示：

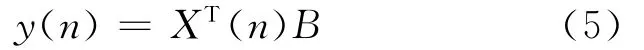
式中：B为记忆多项式的系数矢量；XT（n）和y（n）分别为系统在采样时刻n时的输入矢量和输出标量。B和X（n）分别定义如下：

根据上面的分析，该预失真器的主要结构是一个矢量内积模块，如图7所示。

图7 记忆多项式预失真器硬件结构图

为了得到预失真器的输出y（n），首先需要计算得到输入矢量信号X（n），这需要进行18次乘法。但是从记忆多项式展开式中可以发现，｜x（n）｜4可以通过2个｜x（n）｜2相乘得到；x（np－1）｜x（n－p－1）｜k－1可以通过x（n－p）｜x（n－p）｜k－1延时1个时钟单位得到，不需要重新计算。经过这样的处理，可以构造如图8所示的硬件结构，得到一次输入矢量信号只需要进行4次乘法运算，大大节省了硬件资源。在实现过程中采用流水处理，故输入矢量信号X（n）较输入信号x（n）有3个时钟单位的延时。

然后通过矢量内积模块来计算预失真器的输出y（n）。其中记忆多项式的系数矢量B由PC机通过串口下载到该预失真器模块的RAM中，运算时读取。矢量内积模块采用二叉树求和的方式，如图9所示。首先需要计算求和项，这里采用并行处理的方式，在求和过程中采用流水处理，求和项共有9项，因此求和过程的延时有［log29］＝4个时钟单位。综合以上分析，可以得知预失真器的输出较之所对应的输入信号有8个时钟单位的延时。

图8 计算输入矢量结构图

图9 矢量内积的二叉树求和

在完成了预失真器的软硬件设计和仿真之后，对整个预失真系统进行了测试。利用Agilent抓图工具，得到预失真前后的两幅频谱图如图10、图11所示。

可以看到，预失真后信号邻道干扰抑制近18 dB，这与极少数硬件实现预失真器，抑制15 d B的结果相比，性能有较大提高，说明设计的预失真系统能够有效抑制邻道干扰，非线性补偿效果明显。

图10 无预失真模块功放输出信号频谱

图11 整个预失真系统输出信号频谱

5 结束语

本文讨论了基于记忆多项式模型的数字预失真器的仿真和实现，仿真结果和测试数据表明，该预失真器设计合理，结构简单，易于进行数字信号的实时处理，能够有效抑制邻道干扰18 d B，预失真补偿效果显著，为国内预失真产品的开发和推广提供了实践参考。

［1］ 佟学俭，罗涛．OFDM移动通信技术原理与应用［M］．北京：人民邮电出版社，2003．

［2］ 冯永生．预失真射频功率放大器的研究［D］．北京邮电大学博士研究生学位论文，2007：71－77．

［3］ 钱业青，姚天任．记忆非线性功率放大器的神经网络预失真［J］．计算机工程与应用，2004，（21）：100－103．

［4］ L．Ding，G．T．Zhou，D．R．Morgan．A Robust Digital Baseband Predistorter Constructed Using Memory Polynomials［J］．IEEE Trans．on Communications，2004，52（1）：159－164．

［5］ Eun C S，Powers E J．A New Volterra Predistortor Based on the Indirect Learning Architecture［J］．IEEE Trans on Signal Processing，1997，45（1）：223－227．

［6］ S Cripps．RF Power Amplifiers for Wireless Communications［M］．Artech house，1999．