两种解模糊方法解模糊能力比较

刘庆云， 曹 菲

（1．上海无线电设备研究所，上海200090；2．第二炮兵工程学院，陕西 西安710025）

0 引言

相位干涉仪具有较高的测向精度，是电子侦察领域普遍采用的一种测向方法。为解相位模糊，干涉仪测向系统通常采用多基线技术［1－6］，但这是以设备量的成倍增加为代价的。在设备量及安装体积非常受限的情况下，双基线干涉仪测向系统自然倍受青睐。基于余数定理和虚拟基线技术解相位模糊是双基线干涉仪可供选择的解模糊方法。那么，哪种解模糊方法的解模糊能力更优呢？这是本文要回答的问题。

1 两种解相位模糊方法的基本原理

1．1 基于余数定理解相位模糊的原理

图1为双基线干涉仪基于余数定理解相位模糊的原理示意图。

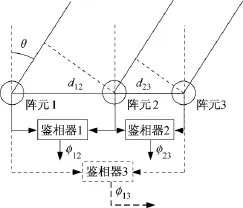
图1 双基线干涉仪解相位模糊原理示意图

图中，天线单元1与2、2与3分别构成基线1、2，相应的基线长度及鉴相器的无误差输出分别为d12、d23（d12／d23＝p／q，p、q为互质数）、φ12、φ23（当考虑鉴相误差时，则将φ12、φ23分别记作φ＾12、φ＾23）；θ、λ分别为来自远场的电磁信号的到达角及信号波长。由图1可得

式中：k01、k02分别为对应于基线1、2的相位模糊值。工程应用中，通过对式（4）中的k1、k2进行二维搜索的方法寻找的最小值，该最小值所对应的k1、k2即为真实的相位模糊值。这就是双基线干涉仪基于余数定理解相位模糊的原理，可表示为

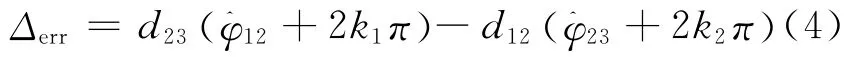
1．2 虚拟基线解相位模糊原理

由式（1）、式（2）可得

显然地，当 d12－d23＜λ／2时，可由式（5）推得式（6）：

式（6）说明，可由d12、d23构造一个虚拟短基线。当该基线长度时，一定可由该短基线获得θ的无模糊粗估计值。然后，再由相应的长基线提高估值精度。这是虚拟基线技术解相位模糊的原理。

2 解模糊能力比较

比较条件：

b）基于余数定理解模糊时，d12＝0．36m，d23＝0．11m；

c）基于虚拟基线解模糊时，d12＝0．24m，d23＝0．23m。

图2示出了相同信噪比条件下，两种解模糊方法错误解模糊百分比（错误解模糊次数与总仿真次数之比，并用百分数表示）与信号波长间的关系曲线（5 000次独立仿真计算的统计结果）。

鉴于基于虚拟基线解模糊时，两基线长度同样满足互质数条件，图2中也给出了此种基线配置情况下，利用余数定理所得解模糊结果，并记作余数定理解模糊1。由图2可见：

图2 两种解模糊方法解模糊能力与信号波长间的关系曲线

a）当基线配置满足虚拟基线条件时，两种解模糊方法的解模糊能力基本无差异，且均与信号波长无关；

b）当d12＝0．36m、d23＝0．11m时，余数定理解模糊方法的解模糊能力随信号波长的增大而增大；

c）相对于余数定理解模糊方法，虚拟基线解模糊方法应当是不可取的。

3 结束语

综上所述可见，虚拟基线解模糊方法的解模糊能力是比较差的；在相同基线配置情况下，余数定理和虚拟基线解模糊方法的解模糊能力基本无差异；仿真结果验证了这两个结论。尽管直观感知告诉人们，随着信号波长的增大，各种解模糊方法的解模糊能力应当越来越高，但仿真结果却表明，当基线配置满足虚拟基线条件时，两种解模糊方法的解模糊能力不随信号波长的增大而增大。这似乎表明，当双基线干涉仪的基线配置确定时，其解模糊能力也就随之确定了。进行合理的基线配置，并使用基于余数定理的解模糊方法是一种比较好的选择。

［1］ 司伟建，初萍．干涉仪测向解模糊方法［J］．应用科技，2007，34（9）：54－57．

［2］ 林以猛，等，宽带信号的数字测向算法研究［J］．南京航空航天大学学报，2005，37（3）：335－340．

［3］ 李建军．多基线干涉仪测向的基线设计［J］．电子对抗，2005（3）：8－11．

［4］ 张勇，刘渝．多信号数字测向算法研究［J］．数据采集与处理，2002，17（3）：265－270．

［5］ 周亚强，陈翥，皇甫堪，等．噪扰条件下多基线相位干涉仪解模糊算法［J］．电子与信息学报，2005，27（2）：259－261．

［6］ 宋才水，顾尔顺．无模糊长基线干涉仪测角的设计［J］．现代防御技术，2006，34（2）：52－54．