基于改进的差分进化算法的非均匀阵列综合
2012-12-01宋晓侠郭陈江
宋晓侠,郭陈江,丁 君
(西北工业大学电子信息学院,陕西 西安 710129)
0 引言
在许多工程应用中,通常要求阵列天线要有窄的扫描波束和低的副瓣。同均匀阵列天线相比,非均匀阵列天线自由度更大,因而能在减少天线阵列建造成本、降低系统复杂度的同时,满足工程要求[1]。
非均匀阵列天线的综合问题(给定阵元数和阵列响应,确定位置和激励分布)一直未得到很好的解决。由于非均匀阵列天线的最大相对旁瓣电平是阵元位置的非线性函数,没有现存的解析方法来确定最大相对旁瓣电平,也就是说,即使已知所有阵元的位置,也没有可凭借的解析方法来求得最大相对旁瓣电平出现的位置,因而阵元间距的优化是一个非线性问题[2],一直都是非均匀阵列天线研究的难点和重点。
虽然已有许多经典的优化方法(如微扰法、穷举法及统计法等)可以借用,但随着计算机技术的发展和天线系统变得复杂,越来越多的优化方法用于阵列天线的综合,常见的有共扼梯度法、拟牛顿法、神经网络、单纯形法、遗传算法和模拟退火法。差分进化算法(Differential Evolution,DE)是由 R.Stone和K.Price在1995年提出的一种简单而高效启发式的全局优化算法[3],在1996年的国际进化优化竞赛上,DE表现优异,被证明是最快的进化算法之一。差分进化算法具有参数少、算法简单、易编程等优点,对于高维、非线性及不可微等特性的函数优化问题表现出极强的生命力,因而广泛应用于各个领域。与遗传算法相比,收敛速度更快,且易于其他方法相结合[4],而且此算法无论在数学还是在天线阵列优化[4-5]方面都有很好的鲁棒性。标准的DE算法一个重要缺陷就是在求解后期收敛速度较慢,对于有些多峰复杂函数容易出现“早熟”现象,文献[6]针对这一缺点设计了一种快速高效的差分进化算法。目前该改进算法尚未在天线领域中应用,因此,将该改进的差分进化算法引入到非均匀线阵综合。
1 优化模型及差分进化算法
考虑优化的不对称非均匀线阵如图1所示,阵列的孔径为L,阵元数为N(N为正整数),为了保证阵列的孔径为L,令dN=L,d1=0,取阵元位置为(d2,…,dN-1),满足 min {di+1-di≥d} ,使该线阵的最大峰值旁瓣电平(maxPSLL)最低。取阵元位置为优化变量,且In为第n个电流激励,u=cosθ,θ是扫描角,0≤θ≤π,k=2π/λ,u的取值区间排除主瓣区域,各阵元的激励等副同相,即In=1(n=1,…,N),则非均匀线阵的方向图为:
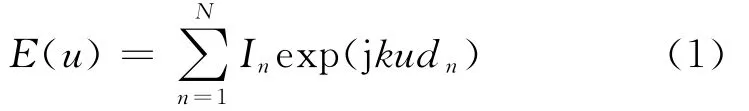

图1 不对称非均匀线阵的结构Fig.1 Geometry of non-uniformly linear asymmetric array
以降低非均匀线阵的峰值旁瓣电平(PSLL)为优化目标,依据最大峰值旁瓣电平构造适应度函数:
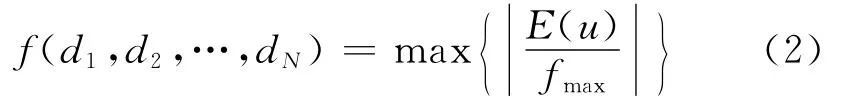
式(2)中,fmax为主瓣峰值。
目标函数为:
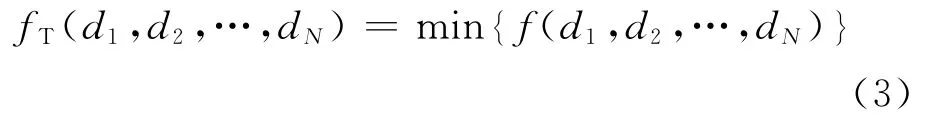
1.1 标准差分进化算法
标准DE算法首先要随机产生一个种群,然后对种群中的个体进行变异、交叉和选择操作,从而产生新的一代,如此反复迭代最终收敛到最优个体[7]。具体操作如下:
1)变异操作
对每个目标矢量变异如下

式中,r1、r2、r3∈ [1,2,…,N]为随机选择的不同于i的互不相同的3个数;di(n)为第n代产生的新个体,F ∈ [0,2]为缩放因子。
2)交叉操作
对于目标矢量di(n),将与式(1)中产生的变异矢量Di(n+1),按如下规则进行交叉产生实验矢量:

式中,R∈[0,1]为交叉概率因子。
3)选择操作
DE在交叉操作之后,通常采用贪婪选择产生如下子代:凡交叉后所产生个体之目标函数优于其父体,就代替父代进入再下一代循环;否持父代不变。
1.2 改进的差分进化算法
针对标准DE算法易陷入早熟的缺点,在变异和交叉操作中引入文献[6]提出的自适应缩放因子F及交叉概率因子R:

式中,Fmax为0.6,Fmin为0.2,Rmin为0.2,Rmax为0.9,nmax为迭代的最大代数。缩放因子F和交叉概率因子R的大小对算法的收敛性和收敛速度有极大的影响。为了在搜索的初始阶段保持种群的多样性,进行全局搜索,而在搜索的后期应加强局部搜索能力和加速收敛速度,以提高算法的精度。该改进DE算法能够很好地平衡局部搜索能力和全局搜索能力。该改进算法的具体步骤如下:
1)创建初始群体;
2)计算群体中个体的适应度;
3)判断是否满足收敛准则,若满足则输出最佳个体,否则继续迭代;
4)自适应变异操作;
5)自适应交叉操作;
6)选择最佳个体作为新父代;转到第2)步骤。
2 用改进的差分进化算法综合非均匀线阵
将该改进的差分进化算法用来综合非均匀线阵,在进化过程中增加了改进DE算法预处理和后处理两个步骤,因而在优化过程中不需要反复测定阵元是否满足条件,简化了优化过程。具体描述如下:
1)初始群体的创建
该直线阵的优化参数即各点源的坐标di,在[0,L]的范围内随机产生,并在优化的过程中不断趋近于最优值。无论是随机产生的还是进化得到的最优值di,都需要测定其是否满足最小间距条件,这样会使优化过程非常复杂。非均匀线阵的约束条件为:为了从物理上保证最大阵列孔径,在两端各放置一个阵元,即,dN=L,d1=0,假设前N-1个阵元都向后占据长度为d,则共有(N-1)d的区间上不能分布阵元,这样孔径上共剩余的区间为:S=L-(N-1)d,在区间[0,S]上随机生成N-2个随机数并按照从小到大的顺序排列,这样即可生成阵元向量:

不难证明,上述方法生成的个体满足了阵元数为N,孔径为L,最小阵元间距为d。再根据上述描述,可以随机生成M个向量X构成初始种群。
2)改进DE算法预处理和后处理
由于阵列的阵元间距约束,通过通用的DE算法交叉变异得到子代群体很有可能不再满足阵元间的距离约束。为了避免该问题的出现,需要对父代群体进行差分操作预处理提取基因信息,然后对基因信息进行自适应交叉和自适应变异两种差分操作,最后对新的基因信息矩阵进行差分操作后处理,得到子代群体。
令由阵元数N和最小阵元间距d确定的数量矩阵为约束矩阵:

定义1:由选择后的形式如F父代群体F1到差分操作(广义交叉和广义变异)前的基因矩阵P的如下变换为DE算法操作预处理:

定义2:交叉和变异操作之后的基因信息矩阵P1到子代群体F2的DE算法操作后处理:

3)改进DE算法的变异和交叉操作
通过预处理得到的父代个体,按照式(4)进行自适应变异操作,产生变异矢量Di(n+1),自适应缩放因子F由式(6)确定。再判断变异矢量是否在[0,S],若不在,将变异矢量用[0,S]区间内的随机数取代,最后对该变异矢量的元素从小到大排列;对于目标矢量和变异矢量按照式(5),产生实验矢量Ui,j,其中自适应交叉因子按照式(7)确定。
3 仿真实例
为了验证改进的DE算法在天线应用中的有效性和稳健性,下面用它综合两例线阵具有不同阵元数同一孔径非均匀线阵,并分别与同一孔径同一阵元数的均匀线阵进行比较。
仿真实例1:对于阵列孔径为9.744λ(λ为波长),阵元数为17,任意阵元间距不小于0.5λ的非均匀线阵。算法的基本参数为:种群数为100,终止代数为300,采用截断选择,截断阀值为0.5。为保证该方法的有效性,随机进行了9次仿真实验,表1列出了优化后的PSLL最优线阵的阵元坐标和阵元间距,PSLL值为-20.080 1dB,图2为最优非均匀线阵和均匀线阵方向图。仿真结果表明:该方法可用于非均匀天线综合,有效地降低阵列天线最大旁瓣电平。

表1 仿真实例优化的阵元坐标Tab.1 The element positions in simulation

图2 阵元数为17均匀阵与非均匀阵方向图比较Fig.2 Comparison of Radiation pattern for the non-uniformly and uniform 17-element array
仿真实例2:图3为阵列孔径为9.744λ(λ为波长),阵元数为10的均匀阵列和非均匀线阵的方向图,算法参数与仿真实例1相同。从图中可以看出,均匀阵列的方向图会出现栅瓣,而DE优化的非均匀阵列没有,因此该方法能有效避免栅瓣。图4为仿真实例的收敛曲线,可以看出该方法具有高鲁棒性,快速达到预期目标。

图3 阵元数为10均匀阵与非均匀阵方向图比较Fig.3 Comparison of Radiation pattern for the non-uniformly and uniform 10-element array

图4 DE收敛曲线Fig.4 Convergence characteristics of DE
仿真实例3:运用遗传算法(GA)综合仿真实例1,GA的基本参数为:种群数为200,最大迭代次数为300,采用截断选择,截断阈值为0.5,单点交叉,交叉概率0.6,变异概率为m =0.3-0.29n/nmax,随机运行9次。图5为DE和GA算法随机运行9次最大旁瓣电平值对比,由图可知,DE算法得到的结果比GA算法更优,算法更加稳定。

图5 GA和DE算法运行9次的maxPSLL对比Fig.5 Contrast of maxPSLL by GA and DE running nine times
4 结论
本文将改进的差分进化算法引入非均匀阵列综合。该改进的DE算法在天线综合过程中,增加了预处理和后处理两个步骤,简化了综合过程。仿真结果表明:该方法能有效地改善其阵列天线的性能,迅速找到最佳阵列天线单元的位置,简单实用,快速有效,鲁棒性和稳定性好,为解决天线综合这一问题提供了有益的参考。
[1]汪茂光,吕善伟,刘瑞祥.阵列天线分析与综合[M].成都:电子科技大学出版社,1989.
[2]Kumar B P,Branner G R.Generalized analytical technique for the synthesis of unequally spaced arrays with linear,planar,cylindrical or spherical geometry[J].IEEE Trans.Trans on Antenna and Propagation,2005,53(2):621-634.
[3]Storn R Price K.Differential evolution-a simple and efficient adaptive scheme for global optimization over continuous spaces[R].US:International Computer Science Institute,1995.
[4]范瑜,金荣洪,耿军平,等.基于差分进化算法和遗传算法的混合优化算法及其在阵列天线方向图综合中的应用[J].电子学报,2004,32(12):1 997-2 000.FAN Yu,JIN Ronghong,GENG Junping,et al.A hybrid optimized algorithm based on differential evolution and genetic algorithm and its applications in pattern synthesis of antenna arrays[J].Acta Electronica Sinica,2004,32(12):1 997-2 000.
[5]Kurup D G,Himidi M,Rydberg A.Synthesis of uniform amplitude unequally spaced antenna arrays using the differential evolution algorithm[J].IEEE,2003,51(9):2 210-2 217.
[6]肖术骏,朱学峰.一种改进的快速高效的差分进化算法[J].合肥工业大学学报,2009,32(11):1 700-1 703.XIAO Shujun,ZHU Xuefeng.A modified fast and highly efficient differential evolution algorithm[J].Journal of Hefei University of Technology(Natural Science,2009,32(11):1 700-1 703.
[7]周艳平,顾幸生.差分进化算法研究进展[J].化工自动及仪表,2007,34(3):1-5.ZHOU Yanping,GU Xingsheng.Development of differential evolution algorithm[J].Control and Instruments in Chemical Industry,2007,34(3):1-5.
