有限元网格剖分与网格质量判定指标

李海峰 吴冀川 刘建波 梁宇兵

1.中国工程物理研究院计算机应用研究所，绵阳，6219002.新加坡国立大学，新加坡，119077

0 引言

随着计算机技术的快速发展和普及，有限元方法已迅速从工程结构强度分析计算扩展到几乎所有的科学技术领域，成为一种应用广泛并且实用高效的数值分析方法。早期有限元分析的研究重点在于推导新的高效率求解方法和高精度的单元。随着数值分析方法的逐步完善和计算机运算速度的飞速提高，整个计算系统用于求解运算的时间越来越短，而数据准备和运算结果的表现问题却日益突出[1]。网格剖分作为建立有限元模型的一个重要环节，要求考虑的问题多，需要的工作量大，不同的网格划分方式会对计算规模、计算结果和计算精度产生很大的影响。故而，对有限元网格剖分的研究十分必要。

有限元分析的最终目的是要还原一个实际工程系统的数学行为特征，即分析必须是针对一个物理原型的准确的数学模型。从广义上讲，模型包括所有的节点、单元、材料属性、几何特性、初始条件、边界条件等，以及其他用来表现这个物理系统的特征。从狭义上讲，模型生成仅指用节点和单元表示空间体域以及实际系统连接的生成过程，即网格剖分。

在建立有限元模型过程中，不管从广义还是从狭义上讲，都涉及网格剖分问题。曾经有人作过统计，在数值分析的三个阶段中，前处理约占总时间的40%～60%，数值求解约占5%～20%，计算结果后处理约占30%[2]。如果纯粹采用人工方法进行分析对象的离散化工作，势必需要花费大量的时间，而且当模型复杂时，还容易出错。前处理工作比较繁琐，但是又十分重要，它是进行有限元正确分析的基础。因此，开展更好的分析对象离散化网格划分工作，对于数值分析工作者来讲，具有非常重要的意义。

1 网格剖分要求

有限元网格生成就是将工作环境下的物体离散成单元的过程，常用的单元包括：一维杆单元及集中质量元，二维三角形和四边形单元，三维四面体、五面体、金字塔形、六面体单元。其边界形状主要有直线型、直面型、曲线型和曲面型。对于边界为曲线(面)型的单元，有限元分析要求各边或面上有若干节点，这样既可保证单元的形状，同时又能提高求解精度、准确性和加快收敛速度。不同维数的同一物体可划分为多种单元混合而成的网格。

网格划分应该遵循以下原则。①合法性。一个单元的节点不能落入其他单元内部，在单元边界上的节点均应作为单元的节点，不可丢弃。②相容性。单元必须落在待分区域内部，不能落入外部，且单元并集等于待分区域。③协调性。单元上的力和力矩能够通过节点传递给相邻单元。为保证单元协调，必须满足：一个单元的节点必须同时也是相邻单元的节点，而不应是内点或边界点；相邻单元的共有节点具有相同的自由度性质，即自由度必须匹配。④逼近精确性。待分区域的顶点(包括特殊点)必须是单元的节点，待分区域的边界(包括特殊边及面)被单元边界所逼近。⑤良好的单元形状[1]。单元最佳形状是正多边形或正多面体。⑥良好的划分过渡性[1]。单元之间过渡应相对平稳，否则将影响计算结果的准确性甚至使有限元计算无法进行下去。⑦网格划分的自适应性[1]。在几何尖角处、应力、温度等变化大的地方网格应密，其他部位应较稀疏，这样可以保证计算结果精确可靠。⑧一致性。对于相连的两个二次单元，单元角点只能与单元角点连接，而不能与相邻单元的中间节点连接；相邻单元的公共边应具有相同的节点数，当采用混合单元(线性单元与高阶单元)类型时有必要从一个单元中除去中间节点。另外，在动力分析中，冲击波传播问题不推荐使用二次单元。

2 网格剖分准备与剖分方法

2.1 网格剖分准备工作

(1)确定合适的网格密度。在数值分析中经常碰到的问题是：单元网格应剖分得如何细致才能获得合理的结果。对于此问题，可借助于以下一些技术解决：①利用自适应网格剖分产生可以满足某种误差估计准则的网格。②与先前独立得出的实验分析结果或已知解析解进行对比。对已知结果和计算结果偏差过大的地方进行网格细化。③执行一个认为是合理的网格剖分的初始分析过程，再在危险区域利用两倍多的网格重新分析并比较两者的结果。如果这两者给出的结果几乎相同，则网格是足够的。如果产生了显著不同的结果，应该继续细化网格直到随后的剖分获得了近似相等的结果。④如果细化网格测试显示只有模型的一部分需要更细的网格，可以对模型使用子模型以放大危险区域。网格剖分密度很重要，如果网格过于粗糙，那么结果可能包含严重的错误，如果网格过于细致，将花费过多的计算时间，浪费计算资源，而且模型过大可能会导致不能在自己的计算机上运行。因而，在生成模型前应仔细考虑网格密度问题。

(2)单元形状与类型的选择[3]。从单元几何形状看，一维分析有两点或三点线单元，二维分析有三角形或四边形单元，三维分析有四面体或六面体单元。四边形单元可以退化成三角形单元，六面体单元可以退化成五面体(楔形或金字塔形)单元或四面体单元，这取决于所分析问题的维数。从数值积分方案看，有全积分和降阶积分之分，取决于分析问题所要求的精度，全积分方案精度高，降阶积分方案精度低。从分析问题的类型看，有结构分析单元与非结构分析单元，不同的节点自由度和不同的场问题控制方程需要采用不同的单元类型，具体有平面应力、平面应变、二维梁、轴对称壳、轴对称实体、三维壳、三维实体、三维梁、热传导单元等。从单元的阶次看，有线性单元(无中间节点)和二次单元(带中间节点)，利用二次单元分析的精度较高，但是由于节点数猛增，会增加计算成本，而且所需存储空间也会成倍增加。

2.2 网格剖分方法[3]

(1)网格直接生成法(直接建模法)。网格直接生成技术并不仅仅只是手动添加单元，而是以单元作为基本构造模块。先用一个个比较大的单元组成一个很粗糙的(待细分)网格体，然后通过特定的工具对这个比较粗糙的网格再进行精细的重新划分，达到所要求的精度。这个生成过程特别适合那些几何模型简单的问题，生成方法简单，大体可分为三个步骤：①生成粗糙构造模块，并对内部进行精细划分，即生成坐标基本合适和具有完全合格的连通性的网格模型，然后在需要的地方重新划分和细分那些单元；②使边界坐标符合要求，即把边界节点坐标更改正确；③重新调整内部网格，即重新分配内部的坐标来生成合理形状或者“放松”的单元。

(2)由几何实体生成网格法(实体建模法)。通过几何实体生成网格，能够将由几何元素描述的物理模型自动离散成有限单元，应用这种技术生成的模型的基本构成模块是几何体而不是网格体。用来表征几何体的几何元素是点、线、面、体，几何模型必须完全建立好之后才能被剖分成网格模型。由几何模型生成网格的方法有很多好处，最主要的优点在于复杂模型通过这种方法容易生成，而通过直接生成法往往很难处理，而且还容易出错。这是该方法适用范围更广的重要原因。通过这种方法，有时还可以使用从其他CAD软件传输过来的模型进行操作，可大大提高效率。

3 有限元网格剖分算法

网格剖分算法主要包含以下几种：拓扑分解法、节点连元法、网络模板法、映射法、几何分解法、基于栅格法、空间编码法[1,4-17]。目前，在许多商业软件中，这些方法基本上是混合使用的，很少有单独使用的，并且这些方法与现代计算机技术结合紧密。

3.1 拓扑分解法

拓扑分解法是由Wordenweber[15]提出的，用于求解二维平面问题，现已推广至三维空间。该方法用一种三角化算法将目标用尽量少的三角形完全分割覆盖，这些三角形主要是由目标的拓扑结构决定，这样目标的复杂拓扑结构被分解成简单的三角形拓扑结构。该方法后来被发展为普遍使用的目标初始三角化算法，用来实现从实体表述到初始三角化表述的自动转换。拓扑分解法原理简单，引入的算子概念使程序易于实现模块化，处理容易。但是该方法只从拓扑关系入手，不考虑几何因素，因此难以保证网格质量，而且检测量很大，对包含曲面的三维形体也难以处理。

Woo等[16]提出了另外一种基于拓扑分解法的有限元网格自动生成算法，试图解决三维实体的有限元网格生成问题，但其网格质量难以得到保证。

3.2 节点连元法

节点连元法主要包括两个步骤：节点生成和单元生成。首先在待分区域内生成一定数目的节点，然后通过适当的算法连接节点生成有限元单元。常用的算法有Delaunay三角剖分法(简称DT法)和推进波前法(advancing front technique，AFT)。

DT法是目前最流行的通用的全自动网格生成方法之一。其最大优点是遵循“最小角最大”和“空球”准则。“最小角最大”是指在不出现奇异性情况下，Delaunay三角剖分最小角之和均大于任何非Delaunay剖分所形成的三角形最小角之和。DT法自动避免了生成小内角的长薄单元，特别适用于有限元网格生成。而“空球”准则是指在剖分的任意三角形单元或四面体单元的外接圆(二维)或外接球(三维)内都不包含其他单元节点。DT法的计算效率与具体实现方法相关。

此网格划分方法是先生成覆盖区域的稀疏三角形单元，然后局部加密，再生成所需密度的三角形网格。所生成的单元形态趋向于等边三角形。DT法充分考虑了几何形状中存在的微小几何特征，并能在微小几何特征处划分较细的单元。在不需要密集网格处，采用稀疏单元，疏密网格的过渡十分平滑。

虽然DT法既适用于二维域也适用于三维域，但直接的DT法只适用于凸域，不适用于非凸域，因此后来又发展了多种非凸域的Delaunay剖分。

近年来，推进波前法也已经成为目前最流行的通用的全自动网格生成方法之一。其基本原理是：设区域的有向离散外边界集和边界前沿点集已经确定，按某种条件沿区域边界向区域内部扣除三角形(四面体)直到区域为空集。AFT的关键技术有两个：区域的边界离散与内部节点合理生成，扣除三角形条件。而扣除三角形条件有多种：最短距离条件、最大角条件、最大形状质量条件、最小外接圆条件等。

AFT可以全自动地在平面或曲面上生成网格，用户可控制生成单元的几何分类：四边形或三角形，或者四边形和三角形混合网格。这种自动计算网格的方法是一次生成一个单元，从区域的边界向内部逐渐生成全域网格。由它生成的网格同样有着很好的几何尺寸和形状且疏密过渡平滑。当网格疏密过渡较剧烈时，它也同样能够生成高质量的网格。

3.3 网格模板法

网格模板法生成单元主要分两步(以三维实体为例)：第一，将待剖分网格的实体用适当大小的立方体(树根)完全包容，按照“一化八”的原则递归离散，通过对每个八分块分类，形成IN和NIO八分块的并集，称为网格模板模型。第二，根据得到的网格模板模型，再进行网格划分处理。

网格模板法的优点是网格生成完全自动，网格剖分速度快，非常适用于自适应网格生成；主要缺点是边界单元形状难于完全保证。另外，网格模板法对物体的方向较敏感。

3.4 映射法

映射法的基本思想是：通过适当的映射函数将待剖分物理域映射到参数空间中形成规则参数域；对规则参数域进行网格剖分；将参数域的网格反向映射回物理空间，从而得到物理域的有限元网格。

当前许多商用有限元网格生成器都以该算法为理论基础。其主要特征是采用了“调配函数”概念。产生的网格整齐划一，非常规则，但同时这也是该法的缺点，尤其是当待划分区域不规则时，如瓶颈形状，得到的网格形状是畸变的。另外，映射法是非全自动方法，必须通过人工交互方式，将剖分对象先剖分成具有简单拓扑关系的子域。但映射法处理曲面问题很有效。

映射法的优点是：算法简单、速度快、单元质量好、密度可控制，它既可生成结构化网格又可生成非结构化网格，既可生成四边形单元网格又可生成六面体单元网格，可用于曲面网格生成，可与形状优化算法集成等。

映射法一般可直接处理单连通域问题，但对于复杂多连通域问题，需要首先用手工或自动方法将待剖分域分解成几何形状规则的可映射子区域，然后在每个子区域内应用映射法。然而在实践中仍有几个难点需要克服：① 如何自动地将复杂的不可映射的待剖分域分解成简单的可映射的子区域；② 如何满足某些物理问题中对网格疏密过渡的要求；③ 如何满足子区域之间的网格相容性要求。

3.5 几何分解法

在产生节点的同时，也确定了节点之间的连接关系的网格剖分方法称为几何分解法。这类算法基于问题域的拓扑几何描述，通过从域中逐个移去单元而生成有限元网格。它较多地考虑了待分域的几何特征，确保生成质量较好的网格单元，通常有两种方法：递归法和迭代法。几何分解法可实现从实体几何描述到初始网格生成之间的自动转换，并允许网格密度变化，但只能通过边界点的分布来控制网格规模，网格质量不高，且很难实现局部自适应加密。

几何分解法的最大优势是离散时考虑了网格的形状和大小，因此，所生成的网格单元形状和分布比较好。但是，这种方法自动化程度比较低，也不利于复杂件的网格生成。

3.6 基于栅格法

基于栅格法(grid-based approach)的基本剖分流程如下：首先用一组不相交的尺寸相同或不同的栅格(cells)覆盖在目标区域上面，保留完全或部分落在目标区域之内的栅格，删除完全落在目标区域之外的栅格；然后对与物体边界相交的栅格进行调整、剪裁、再分解等操作，使其更准确地逼近目标区域；最后对内部栅格和边界栅格(特别是后者)进行栅格级的网格剖分，进而得到整个目标区域的有限元网格。

这种方法预先产生网格模板，然后将要进行网格化的物体加到其上，并在实体内部尽可能多地填充规则的长方体或正方体网格，在实体的边界上根据实体边界的具体特征更改网格的形状和相互连接关系，使边界上的单元尽可能无限地逼近物体的边界形状。这种方法能实现网格生成的自动化，网格的生成速度也非常快，能够生成的单元类型很多，划分简单，效率较高。其最大缺点是物体边界单元的质量较差；另一个缺点是所生成的单元尺寸相近，网格密度很难得到控制。

栅格法首先用交互方式将物体划分为形状简单的子区域，每个子区域分别用定形的网格模板作为规整的部分，再采取适当的措施，使得相邻子区域在结合面共享公共的节点，并且网格相容。

3.7 空间编码法

空间编码法有两个本质属性：阶梯结构和空间可访问性。该法可以实现与实体造型系统的集成，并且容易精整网格质量。大多数实体造型系统都采用树形数据结构进行几何和拓扑描述，在此基础上，Yerry等[18]提出了修正的八叉树法等有限元网格生成算法。

基于修正的八叉树法的空间编码法在问题域内部容易生成高质量的单元，但是边界单元需要进一步处理，以免所生成的单元因质量太差而不适合有限元分析。也有学者将这种方法划归于基于栅格法。

4 网格形状质量判定及指标

4.1 网格质量要求

如果单元都是理想的形状(三角形单元等边，四边形都是正方形，六面体都是立方体等)，那么在计算单元刚度矩阵的时候误差和错误就会很少出现，然而在整个模型中都用理想形状的单元来离散几乎是不可能的事情，尤其是模型非常复杂时，难以全用规则单元来剖分，因此必须在模型不同位置合理设置不同形状的网格，改善网格质量。

网格质量对于数值分析的精度有十分重要的影响，特别对于具有复杂形状的分析对象，尤为重要。对于复杂几何实体和壳，首先要保证网格单元与几何体严格对应；其次保证单元具有高质量。很多时候在进行数值计算过程中，会出现单元质量不合格的警告信息，严重时会因出错而导致计算中断。因此，建立网格质量标准体系，对于数值分析具有很重要的意义。

一般而言，对于不同的数值分析内容网格质量的标准有所不同。对于一般的热传导分析，可以适当降低网格质量标准，而对于一些非线性问题，如大变形、接触、瞬态高速冲击等分析问题，需要高质量的网格。

由于有限元网格的质量直接影响到数值求解的精确度和正确性，自动生成的初始网格的质量并不总是令人满意的，所以通常要对初始网格的质量进行改进或优化。网格质量的改进可分为两个方面[18]：一是拓扑关系的调整；二是节点位置的调整。

检查网格质量，首先应该检查是否有重复的节点和单元。如果在同一位置需要建立两个节点或单元，应务必小心。在绝大部分商业工程分析软件中，具有在一定公差范围内消除重复节点的功能，如果需要在同一位置产生不同节点(如接触问题)，应避免使用此功能。

4.2 一维网格质量评价指标

一维网格质量评价指标包括自由端点和刚性单元，即检查网格内是否存在自由端点和刚性单元。其中，自由端点主要检查是否存在自由端点或自由节点(即与其他单元不相连)，在一维单元容易出现这个问题，如质量集中单元等。刚性单元主要检查是否具有形成环状的刚性单元。

4.3 二维网格质量评价指标

二维单元的几何形状主要是三角形和四边形，主要质量指标包括：单元长度、翘曲角、单元边长比、内角大小、扭曲角、雅可比比率(Jacobian ratio)等。

三角形单元主要检查：单元长度、长宽比、扭曲角和内角大小。

四边形单元主要检查：单元长度、翘曲度、长宽比、扭曲角、雅可比比率、弦偏离度。

各项技术质量指标如下所述。

(1)单元边长比γAR。γAR为单元最大边长与最小边长之比，适用于所有单元。对单元尺寸应进行适当控制，既保证计算精度，又不浪费资源。理想的单元是单元边长比为1，对线性单元来说，可接受的单元边长比的范围是0<γAR<3，对二次单元来说，可接受的单元边长比范围是0<γAR<10。对于同样形状的单元来说，高阶单元对于边长比没有线性单元对于边长比那么敏感。单元在非线性分析中对于边长比的敏感程度要比在线性分析中对于边长比的敏感程度高。如果一个问题在某一方向应力梯度很大，单元有可能需要相当大的边长比，最小边放在梯度最大的地方。这是因为在一个单元内，如果某一边的梯度很大，这一边又很长，那么误差就会很大。

(2)三角形单元内角。即三角形三个内角大小。

(3)三角形单元扭曲角。这一指标表征了单元在单元面内的扭曲程度。其定义为：对应边中点连线的夹角中最小角的余角，即三角形单元扭曲角θskew=90°-min(α1,α2,α3)，α1、α2、α3为中内角，见图1。另外还有一种定义：单元相邻边夹角与60°之间的差值。

图1 三角形单元扭曲角定义

(4)四边形单元扭曲角。该指标的定义为：对应边中点连线的夹角中最小角的余角，即四边形单元扭曲角θskew=90°-min(δ1,δ2)，见图2。另外一种定义是：单元相邻边夹角与90°之间的差值。

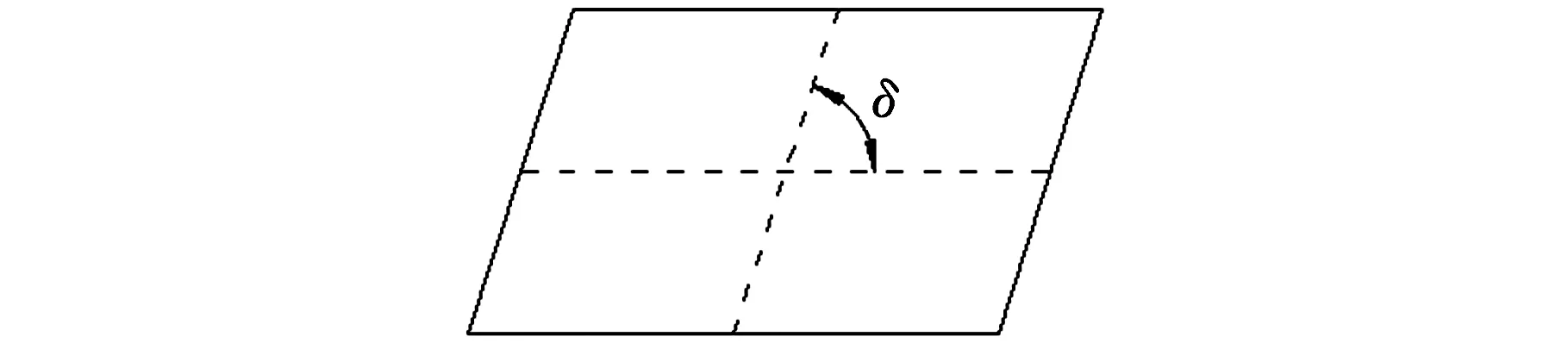
图2 四边形单元扭曲角定义

(5)四边形单元翘曲角。该指标表征了单元在单元的面外的翘曲程度，面外翘曲发生在单元面的节点不共面的时候。其定义如下：依次沿对角线将四边形分为两个三角形，寻找这两个三角形所在面构成夹角的最大值，该角即为翘曲角，即θwarp=max(α1，α2)，见图3。

图3 四边形单元翘曲角

(6)弦偏离度。即单元各边中点与各点在对应边上的投影点的距离值，见图4中的L1、L2。

图4 四边形单元弦偏离度

(7)雅可比比率。即单元内各个积分点Jocabian行列式值中的最小值与最大值之比，见图5。计算公式如下：

(1)

式中，JR为雅可比比率；|J|min、|J|max分别为最小和最大雅可比行列式值。

且

|J|(-1，-1)=(x2-x1)(y4-y1)-
(x4-x1)(y2-y1)=l1l4sinθ1

(2)

式中，x2、x1、y4、y1、x4、x1、y2、y1、l1、l4、θ1参见图5c。

(a)规则四边形单元积分点示意图(b)任意直边四边形单元积分点示意图

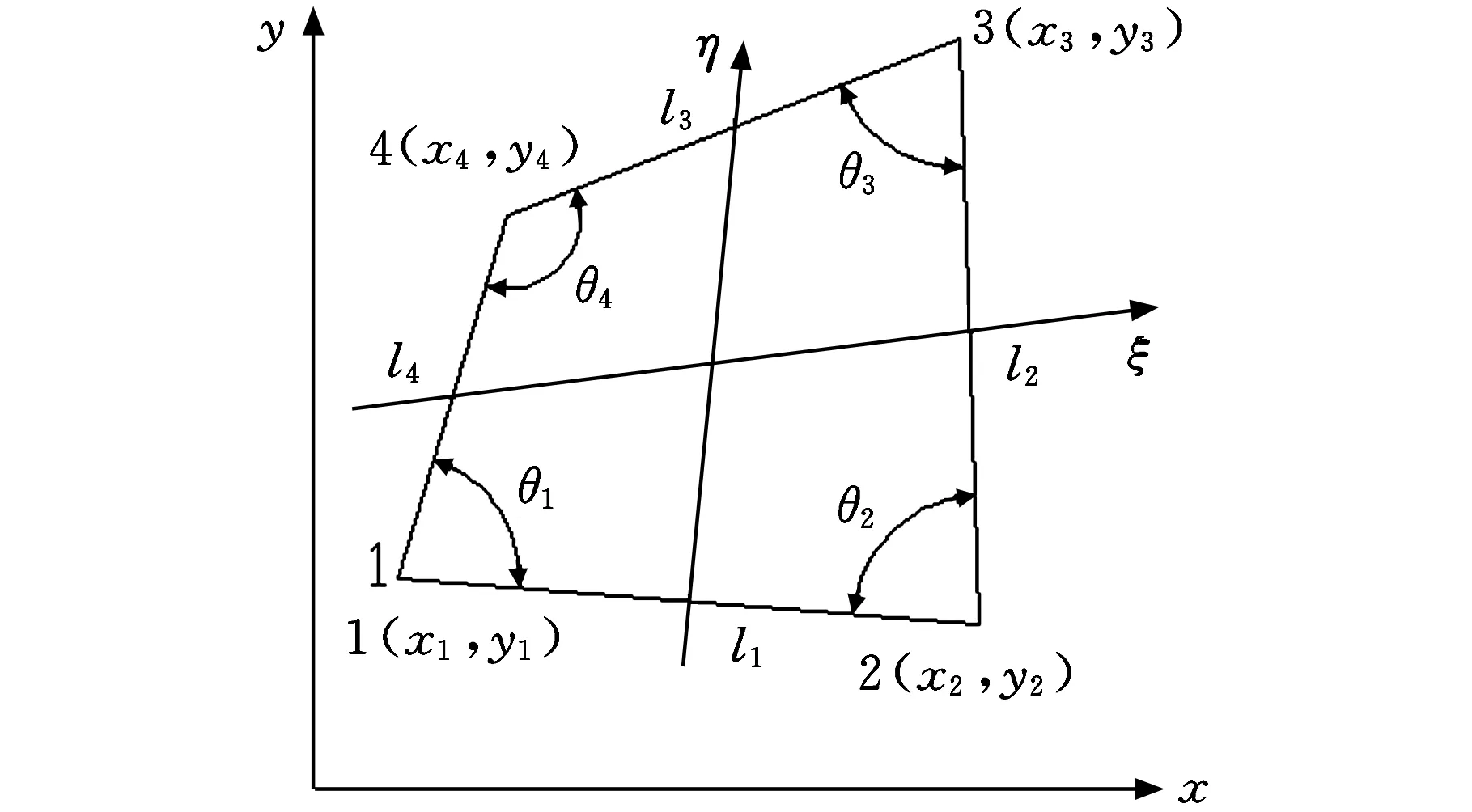
(c)任意直边四边形单元整体坐标

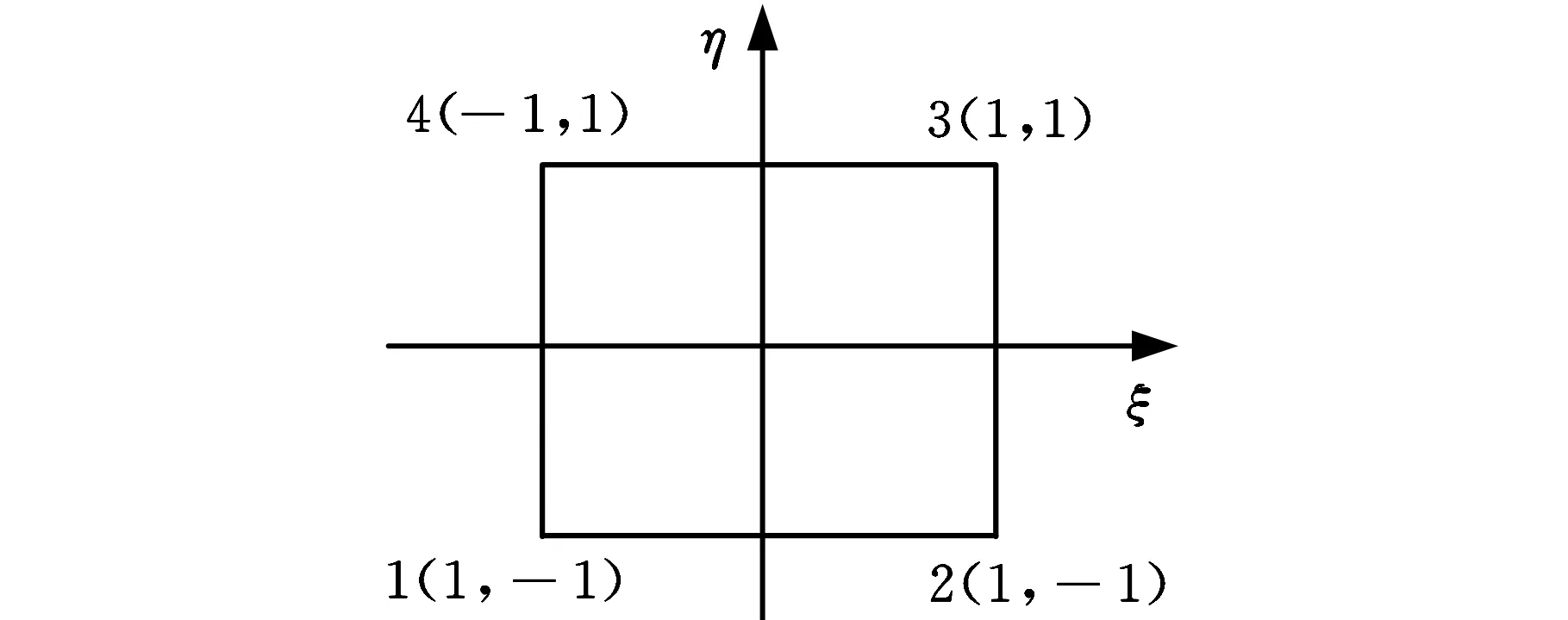
(d)任意直边四边形单元局部(自然)坐标图5 四边形单元雅可比计算示意图

4.4 三维网格质量评价指标

三维单元质量检查指标与二维单元质量检查指标大同小异，但有些指标不一样，如在四面体中，边长比定义为单元最长边与最短高之间的比值，见图6。对于六面体单元，单元质量检查指标与二维单元差不多，但对于四面体单元，还需要另外检查如下几个指标：

(1)四面体单元坍塌(collapse)值。如图7所示，其计算公式如下：

Tcollapse=min(hi/sqrt(Ai))/1.24i=1,2,3,4

式中，hi为各个顶点到对应面的距离值；Ai为对应面的面积；sqrt(·)为取平方根运算的函数。

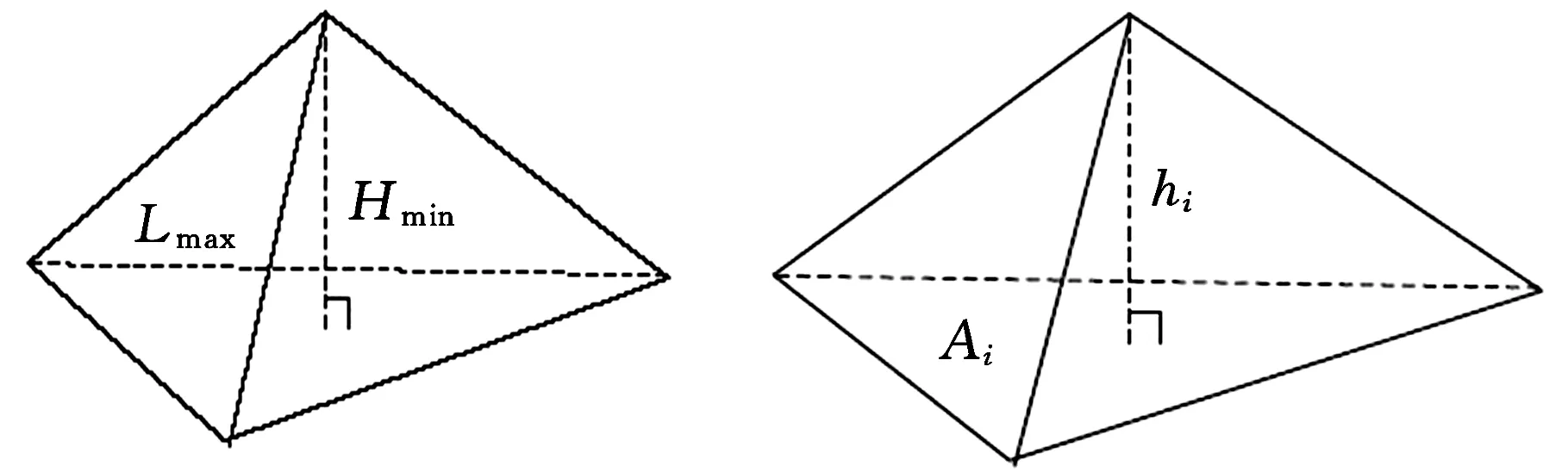
图6 四面体单元边长比示意图图7 四面体单元坍塌值计算示意图

(2)四面体单元的体积扭曲(skew)值。对于任意一个四面体单元，定义一个过该四面体四个顶点的外接球体，如图8所示，再依照球体的半径，计算出一个理想四面体的体积，该体积假定为Videal，实际四面体单元的体积为Vactual，参照理想四面体的体积，按照下面公式计算，就可以得到四面体单元的扭曲值：

Tvolumetric_skew=(Videal-Vactual)/Videal

式中，r为外接球的半径。

图8 四面体单元体积扭曲值计算示意图

5 有限元网格质量优化

5.1 网格优化

为了保证有限元分析结果令用户满意，有限元网格通常应具备以下条件[8]：①所有单元接近理想形状；②主要变量(温度、速度等)变化梯度较大的地方网格密度较大；③粗细网格之间过渡均匀。但通常情况下，在有限元网格自动生成器所产生的网格中总存在一些畸形单元，问题域越复杂，畸形网格所占比例越大。

网格优化目的是改变网格质量，提高计算精度。目前主要存在两种优化方法[8,19]：①网格精整。根据网格密度和计算结果的要求对网格进行细分；②光滑处理。保持网格拓扑关系不变，通过摄动单元节点位置来改善网格质量。

Laplacian光滑处理技巧是应用得最早，也是最成熟的一种优化方法[20]。其核心内容为：保持网格拓扑关系不变，将整个内部节点的位置摄动到由其相邻节点组成的多边形的质心处，使每个单元更接近于理想形状。将这个摄动过程遍历所有内部节点若干次，可较大幅度地提高网格质量。经过Laplacian光滑处理的网格，不再具有Delaunay三角剖分的基本性质。

近年来出现了各种各样的网格优化方法，自适应网格精整方法即是其中之一。首先用较稀疏的网格进行有限元分析，根据计算结果，通过某种误差指示器判断哪些区域的网格需要精整，经局部自适应网格精整后再对该区域进行有限元分析。这样的局部网格精整过程可反复进行多次，直到计算结果满足用户要求为止。

5.2 自适应网格方法

在目前很多数值计算中都需要用到网格自适应技术，如激波产生的高速飞行、材料加工等大变形问题、瞬态高速冲击、炸药爆轰聚能射流及侵彻等。在有限元分析中，网格自适应是在现有的网格基础上，根据有限元计算结果估计计算误差、重新剖分网格和再计算的循环过程。当计算误差达到预定值时，自适应过程结束。因此，有效的误差估计和良好的自适应网格生成是自适应有限元分析两大关键技术[9,21-23]。就目前国内外研究来看，自适应网格生成从大的方面可分为网格增加技术和网格重划分技术两类。

网格增加技术主要依靠增加自由度总数来提高有限元分析精度。目前，主要采用三种类型方法：h型、 p型和 h-p型[22]。h型使用特别广泛，网格模板模型的网格改进正是利用该法。p型是在保持网格划分不变的情况下，通过提高插值函数的阶数获得更高的求解精度。h-p型是将h型和p型结合的一种方法。h-p型虽然实现不容易，但它却可使收敛速率明显加快。实践表明，在获得同一精度时，上述三种类型收敛速率是按h型、p型、h-p型顺序增大的。

网格重划分技术是根据现有的网格并配合误差估计确定新的节点分布，然后重新划分网格，再计算，重复上述过程直到求解精度达到预定目标为止的过程[21]。目前，网格重划分技术在平面区域已得到了较好的实现。从理论上讲，该原理可扩充到三维实体域，但由于三维实体域难以完全自动地用等节点密度曲面来分割任意实体，因此在三维域的扩充至今仍未实现。实践表明，网格重划分技术比网格增加技术具有更多的优点，如收敛速度快、网格单元形状稳定等。

6 网格剖分前处理软件及其应用状况[24]

有限元技术的特点决定其前处理过程为一个相对独立而又十分重要的部分。随着众多有限元商业软件的出现，前处理技术也得到了迅猛的发展，同时很多专业的前处理软件也应运而生。目前，在国际上被认可的前处理软件主要包括Altair公司的HyperMesh，MSC公司的Patran，EDS公司的FEMAP，SamTech公司的Samcef/Field，CAE-Beta公司的ANSA，CFDRC公司的CFD-GEOM和CFD-MicroMesh，TrueGrid，Fluent软件中的Gambit等，还有一些大型有限元商业软件自带有网格剖分器，如Marc/Mentat、Ansys/PreProcesser等。在一般情况下，前处理软件都与CAD软件具有良好的接口，且与众多的有限元求解器结合，可使用户更快、更方便地解决问题。一些大型企业都采用了适应自己需求的前处理软件。

当前，应用最广泛的前处理软件首推HyperMesh，它是一款高效率的有限元前处理软件，可与大多数的有限元分析软件搭配使用，如Marc、Nastran、Abaqus、Ansys、Ls-Dyna等。HyperMesh主要用于汽车行业，它已经成为全球汽车行业的标准配置，几乎所有的整车厂商都在使用。同时HyperMesh也广泛进入各行各业，如航空、航天、通用机械与日用品等行业。

MSC公司的Patran软件是一个集成的并行框架式有限元前处理及分析仿真系统，最早由美国宇航局(NASA)倡导开发，是工业领域最著名的软件系统。其开放式、多功能的体系结构可集工程分析、结果评估、用户化设计和交互图形界面于一身，构成一个完整的CAE集成环境。Patran的用户主要集中在航空、航天、汽车和通用机械等领域。

FEMAP是一个纯Windows风格的、非常易于使用的高性能有限元前处理软件。FEMAP提供给工程师和分析人员一个可以容易、精确、有效地操控复杂模型的前处理手段。FEMAP从高级梁造型、中面提取和高级网格划分，到功能卓越的直接访问CAD工具和简化工具，都提供了有效的方法。

Samcef/Field系列软件的前处理工具是一个独立的图形环境，具有几何建模、读取主流CAD模型和驱动Samcef线性求解器的能力。

ANSA(automatic net-generation for structure analysis)是希腊BETA CAE System公司的软件产品，是世界上广泛应用的、功能强大的前处理系统和三维网格软件工具。ANSA起源于汽车工业领域，主要是为了满足有限元前处理对时间的需求。ANSA已成为工业标准，而且在汽车、航空航天和化工等工业领域应用广泛。

CFD-MicroMesh是为微电子和微机电工业领域的特殊需求而开发的软件系统。它直接从EDA布局图和初始设计开始，是自动化的三维几何创建和网格生成工具。

TrueGrid是美国XYZ Scientific Applications公司推出的专业通用的网格划分前处理软件，支持大部分有限元分析及计算流体动力学(CFD)软件，可以方便快速生成优化的、高质量的、多块结构的六面体网格模型。TrueGrid支持一般CAD所输出的几何形状，如AutoCAD、Pro/E、I-Deas等；支持多款当今主流的分析软件，如Ansys、Abaqus、Adina、Ls-Dyna、Autodyn、Marc、Nastran和流体动力学分析软件，如与Fluent、AutoReagas、CFX、CFdesign、Star-CD、Phoenics、Numeca、Tascflow等具有接口。

Gambit是帮助分析者和设计者建立并网格化计算流体力学模型和其他科学应用而设计的一个软件包，是面向CFD分析的高质量的前处理器，其主要功能包括几何建模和网格生成。由于Gambit所具有的强大功能，在目前所有的CFD前处理软件中，Gambit稳居上游。Gambit通过它的用户界面(GUI)来接受用户的输入，能直接建立模型、网格化模型、指定模型区域大小等，这对很多的模型应用已足够。

目前，国外很多厂商主要以HyperMesh和ANSA作为划分网格与前处理的工具标准。

7 网格剖分实际案例

利用HyperMesh软件平台，笔者进行了二次开发，对几个复杂模型进行了网格剖分。该软件具有先进的网格剖分与网格优化算法，能自动对网格进行光滑、优化处理，改善网格质量，能进行完备的网格质量检查，具备强大的网格编辑功能，可以方便调整、编辑网格，以改善网格质量。

实例一汽车发动机活塞的网格剖分(图9),使用了网格生成映射法和直接建模方法。公司提供如下的网格质量与技术要求：①总的单元数量为50 000～60 000个；②在缸体内壁面上不能出现三角形单元；③90%以上的单元是八节点六面体单元；④单元必须是六面体单元和五面体楔形单元；⑤网格质量指标为θwarp<30°，γAR<5，θskew<60°，JR>0.3；⑥不能出现破裂和T形连接。

图9 汽车发动机汽缸活塞六面体网格模型

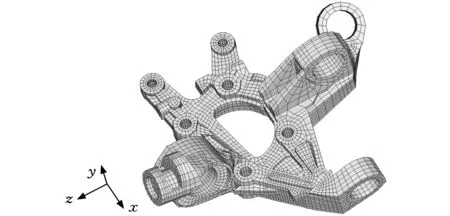
图10 复杂模型六面体网格模型

实例二某复杂模型网格剖分(图10)，综合使用了几何分解法、推进波前法和直接建模法。网格剖分要求为：①总的单元数量为20 000～30 000个；②95% 以上的单元是八节点六面体单元；③单元形状必须是六面体单元或五面体楔形单元；④网格质量指标为θwarp<40°，γAR<4，θskew<50°，JR>0.5；⑤不能出现破裂和T形连接。

实例三汽车转向盘网格剖分(图11)，使用DT法。其网格质量与技术要求为：①全部用四面体单元；②单元数量为30 000～40 000个；③网格质量指标为单元边长小于6mm，γAR<4，θskew<50°，JR>0.5；④不能出现T形连接。

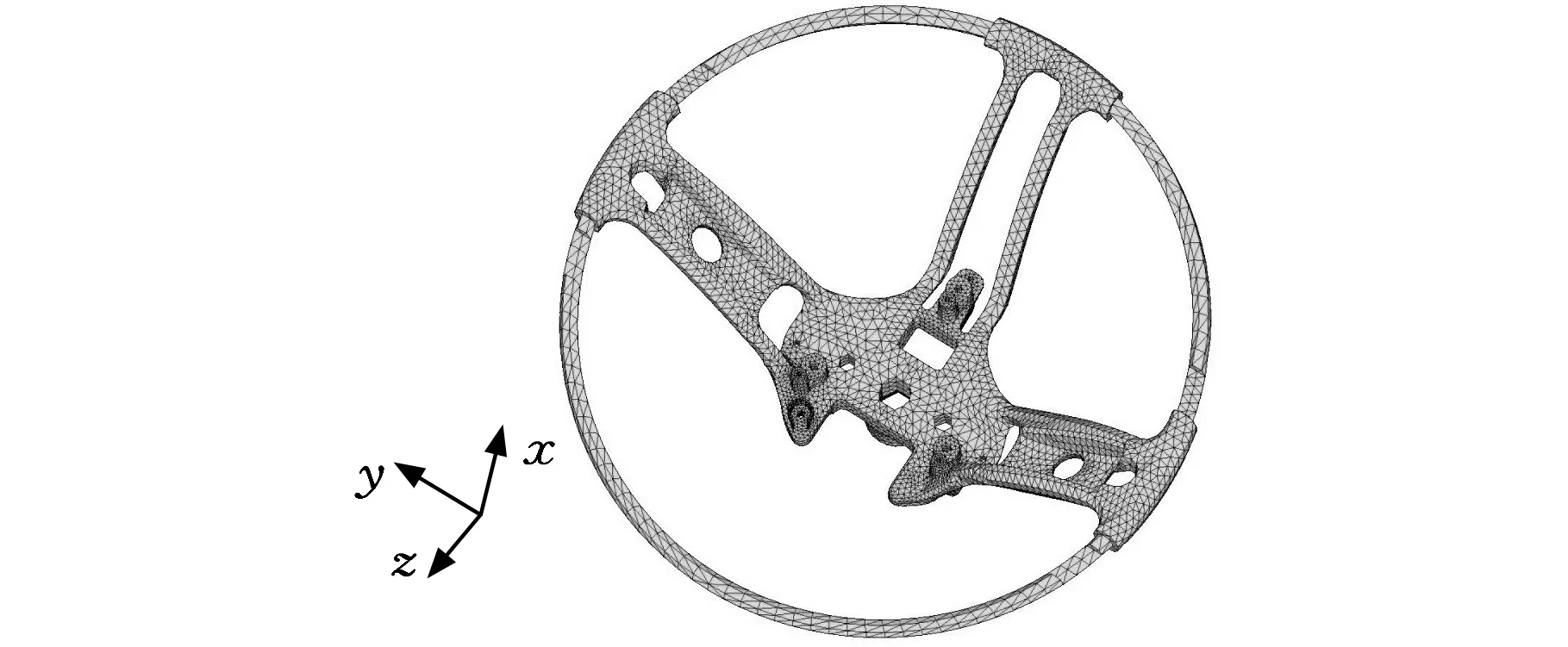
图11 汽车方向盘四面体网格模型

8 网格剖分前处理技术发展趋势

(1)通用算法的数据结构与多种算法的联合应用[1]。在通用算法的研究方面，应注意数据结构的研究和多种算法的联合应用，提高核心算法的可靠性和几何适应性，达到速度与质量之间的平衡，实现核心算法的黑箱化。

(2)根据所分析问题的物理特性对网格进行修改，从这个角度出发有两个主要的问题：生成具有所有性质或部分性质的网格，对现有的网格进行修改以获得所期望的性质，其中自适应有限元分析是一个最为主要的研究领域[25]。

(3)自适应网格剖分技术。自适应算法中通过自动加密网格来提高计算精度，这种算法有效而且收敛速度快，在各个领域内自适应算法将会有较大的发展，其主要问题在于如何进行误差估算。这对于各个领域中的不同问题是不一样的，这也是目前有限元前处理技术发展的主要方向之一。

(4)六面体网格自动剖分技术。几十年来，众多学者致力于六面体单元网格自动生成方法研究，但复杂三维实体的全六面体单元网格全自动生成问题始终未能获得真正意义上的解决。近几年来，全六面体网格自动生成再度成为焦点问题[26-33]。

(5)网格生成算法的并行化和分布化。并行化计算环境对于大规模、超大规模科学计算以及高端工程应用是必需的，而分布式计算环境可作为一种中端工程应用解决方案。现有网格生成并行化或分布化算法在计算效率、内存管理、生成单元质量等方面还不够完善，还有许多潜力可挖。另外，并行计算环境与分布式计算环境的控制软件日趋成熟，这为算法的并行化、分布化开发提供了更强有力的技术保障。

9 结语

数值分析已经与理论研究、实(试)验研究成为三大研究技术手段之一，在计算机技术高度发展的今天，这种手段将会发挥越来越大的作用。采用离散化方法对研究对象进行网格剖分是数值模拟前处理的核心问题。研究网格剖分方法、建立网格质量标准及技术要求体系对于有限元分析具有重要意义。在数值模拟应用日益广泛的今天，必须更加深入研究网格剖分技术方法，建立网格质量标准及技术要求体系。

[1] 王明强，朱永梅，刘文欣.有限元网格划分方法应用研究[J].机械设计与制造，2004(1): 22-24.

[2] Shephard M S. Approaches to the Automatic Generation and Control of Finite Element Meshes[J]. Applied Mechanics Review,1998,4(4):169-185.

[3] 郑岩，顾松东，吴斌.Marc 2001从入门到精通[M].北京：中国水利水电出版社，2003.

[4] 吕军，王忠金，王仲仁.有限元六面体网格的典型生成方法及发展趋势[J].哈尔滨工业大学学报，2001，33(4)：485-490.

[5] 古成中，吴新跃，有限元网格划分及发展趋势[J].计算机科学与探索，2008，2(3), 248-259.

[6] 关振群，宋超，顾元宪，等.有限元网格生成方法研究的新进展[J].计算机辅助设计与图形学学报，2003，15(1)：1-14.

[7] Ho-Le K. Finite Element Mesh Generation Aethods:a Review and Classification[J].Computer-Aided Design,1988,20(1):27-38.

[8] 李俊，游理华.有限元网格自动生成算法的研究进展[J].机械研究与应用，1998，11(4)：25-27.

[9] 李卫民.有限元网格生成算法的评述[J].泰州职业技术学院学报，2004，4(1)：12-14.

[10] 胡恩球，张新访，向文，等.有限元网格生成方法发展综述[J].计算机辅助设计与图形学学报，1997，9(4)：378-383.

[11] 张建华，叶尚辉.有限元网格自动生成典型方法与发展方向[J].技术研究，1996(2):28-31.

[12] 闵卫东，唐泽圣.有限元网格划分技术[J].计算机研究与发展，1995，32(7)：37-42.

[13] George P L.Automatic Mesh Generation. Applications to Finite Element Methods[M]. New York: Willey,1991.

[14] Lohner R, Juan R C. Parallel Advancing Front Grid Generation[C]//Proceedings of the 8th International Meshing Roundtable. Sout Lake Tahoe,CA,1999:67-74.

[15] Wordenweber B. Finite Element Mesh Generation[J]. Computer-Aided Design,1984,16(5)：15-20.

[16] Woo T C, Thomasma T. An Algorithm for Generating Solid Element in Objects with Holes[J]. Comp. Struct., 1984, 18(2)：30-36.

[17] Ruppert J, Seidel R. On the Difficulty of Triangulating Three-dimensional Nonconvex Polyhedra[J]. Discrete & Computational Geometry, 1992,7(3):227-253.

[18] Yerry M A,Shephard M S.Automatic Three Dimensional Mesh Generation by the Modified-octree Technique[J].Int. J. Num. Methods. Eng.，1984,20(11)：1965-1990.

[19] 黄志超，包忠诩，周天瑞，等.有限元网格划分技术研究[J].南昌大学学报，2001，23(4)：25-32.

[20] Huang C Y. Recent Progress in Multiblock Hybrid Structured and Unstructured Mesh Generation[J].Computer Methods in Applied Mechanics and Engineering, 1997,150(1/4):1-24.

[21] Almeida R C, Feijo R A, Galeao A C,et al.Adaptive Finite Element Computational Fluid Dynamics Using an Anisotropic Error Estimator[J]. Computer Methods in Applied Mechanics and Engineering, 2000,182(4):379-400.

[22] Fuenmayor F J,Restrepo J L,Tarancn J E, et al. Error Estimation and H-adaptivere Finement in the Analysis of Natural Frequencies[J]. Finite Elements in Analysis and Design, 2001, 38(2):137-153.

[23] 单菊林.自适应有限元网格生成算法研究与应用[D].大连：大连理工大学，2007.

[24] 于开平，周传月，谭惠丰,等.HyperMesh从入门到精通[M].北京：科学出版社，2005.

[25] 罗特军，罗季军，汪榴.有限元网格优化方法[J].四川联合大学学报，1999，3(3)：65-72.

[26] Chrisochoides N, Nave D. Simultaneous Mesh Generation and Partitioning for Delaunay Meshes[J]. Mathematics and Computers in Simulation,2000,54(4/5):321-339.

[27] Liu Shangsheng, Rajit G. Automatic Hexahedral Mesh Generation by Recursive Convexand Swept Volume Decomposition[C]//Proceedings of 6th International Meshing Roundtable.Washington: Sandia National Laboratories,1997:217-2311.

[28] Blacker T.Automated Conformal Hexahedral Meshing Constraints,Challenges and Opportunities[J]. Engineering with Computers, 2001, 17(3):201-210.

[29] Schneiders R, Bunten R. Automatic Generation of Hexahedral Finite Element Meshes[J].Computer Aided Geometric Design,1995,12:693-70.

[30] Schneiders R,Weiler F.Octree-based Generation of Hexahedral Element Mesher[C]//5th International Meshing Roundtable.Washington:Sandia National Laboratories,1996:205-216.

[31] Mller-Hannemann M. Quadrilateral Surface Meshes Without Self-intersecting Dual Cycles for Hexahedral Mesh Generation[J]. Computional Geometry, 2002,22(1/3):75-97.

[32] Takeo Taniguchi, Tomoaki Goda, Harald Kasper, et al. Hexahedra Mesh Generation of Complex Composite Domain[C]//Proceedings of the 5th International Conference on Grid Generation in Computationa Field Simulations. Mississippi:Mississippi State University, 1996:699-707.

[33] 关振群，单菊林，顾元宪.基于转换模板的三维实体全六面体网格生成方法[J].计算力学学报，2005，22(1)：32-37.