中厚板辊式矫直过程模型算法修正与应用

王效岗 黄庆学 胡 鹰

太原科技大学，太原，030024

0 引言

中厚板作为重要的钢铁产品，广泛应用于机械、船舶、化工等国民建设的重要领域。在其生产流程中，矫直是获得平直板材的重要成形环节，其工艺质量直接决定产品品质。辊式矫直工作原理如下：通过交错布置的辊系使板材在运行过程中产生反复的弯曲，在这个过程中，板材的上下表面发生了局部的塑性变形，中心层为弹性变形区，这种独特的变形过程可以有效地提高板材的平直精度、消除残余应力。辊式矫直过程是一个多道次弯曲的弹塑性变形过程，属于非线性问题。到目前为止，国内外学者对辊式矫直过程已做了大量的研究工作，但矫直过程的精度和智能化程度还不够高。矫直过程研究在理论上存在两个重要问题：①矫直过程中材料的变形特性不明确；②矫直过程的理论解析不完善[1-3]。近年来，工程上对金属条材的强韧性、平直度、残余应力均提出了更高的要求，工业生产中也有节能高效智能化的需求，这些现实需求使得辊式矫直理论模型的完善变得十分迫切[4-8]。

现有辊式矫直理论模型弯曲分析中一般对中厚板按材料力学中的简支梁进行简化研究，但此假设影响了矫直过程的精确计算。本文在对辊式矫直理论模型影响因素进行分析的基础上，提出运用分层算法将材料特性和中性层偏移等因素引入到矫直理论模型中，使计算结果更加符合实际。

1 影响辊式矫直弯曲过程计算的因素

1.1 材料特性及包辛格效应

现有矫直理论分析中，弹塑性弯曲变形中的应力沿截面分布规律一般根据材料拉伸压缩实验应力应变曲线确定，并且材料的拉伸和压缩应力应变曲线近似为同一曲线。同时由于矫直特定的加工过程，板材沿厚度方向的各层纤维产生不同程度的拉伸、压缩变形，这些纤维在矫直过程中承受循环载荷的作用，包辛格效应明显。在循环加载下，应力应变曲线有不同的形式，除具有包辛格效应外，还有同向加工硬化、同向加工软化等现象出现，这些都与材料和其组织状态有关。计算时应采用合适的材料模型，否则在计算矫直过程时理论值与实际值会有明显的偏差。把合适的材料模型引入矫直计算过程，对得出精确的过程解是必要的。

1.2 中性层位置

现有矫直理论分析中，将金属材料弯曲认为是简单弯曲，也就是说不计三向应力的影响；同时不考虑拉伸、压缩对应力极限的影响，弯曲时纵向应力极限都按屈服强度取值。此外，假设弯曲变形时材料弯曲中性层与材料厚度中间层重合，截面上各点的位移正比于该点至中性层的距离，横截面仍为平面，变形与断面高度的关系是线性关系，板材内部应力、应变关于中心点对称分布。而在实际弯曲变形中，板材内部应力、应变并非关于中心点对称分布。中性层在板材厚度上的位置必须满足内部应力平衡的条件，这使得弯曲变形时材料弯曲中性层与材料厚度中间层之间会有一个偏移量，由此导致整个矫直过程的计算基础改变了。

2 弯曲过程分层算法的建立

为精细化研究辊式矫直过程，建立精确的矫直计算模型是必要的。弯曲过程的分层算法通过细化解析方法，把矫直计算过程中材料模型和中性层偏移引入到矫直过程的解析算法中。其具体算法建立如下。

2.1 分割层的建立

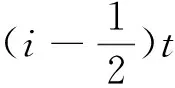
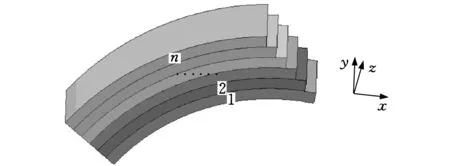
图1 弯曲单元的几何分层

2.2 计算条件

(1)材料模型条件。在热模拟实验基础上，建立循环拉伸压缩力学模型，采用多线段近似应力应变曲线取代实验模型曲线。

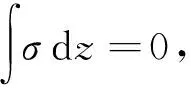
2.3 计算流程

内弯矩计算流程如图2所示，首先，通过矫直机辊系的压下量确定每个弯曲单元的反弯曲率；然后计算每个弯曲单元的内弯矩，在这个过程中，对板材进行分层，对每层进行应力和应变的计算，同时通过迭代计算使整个截面上应力之和等于0；将此弯曲单元的计算结果作为下一个弯曲单元的计算初始条件，在整个矫直计算过程中，分层的情况不发生变化，单元间计算结果的传递也是通过在每层建立独立变量来进行的；计算过程直到所有的弯曲单元全部计算后结束；最后输出数据。

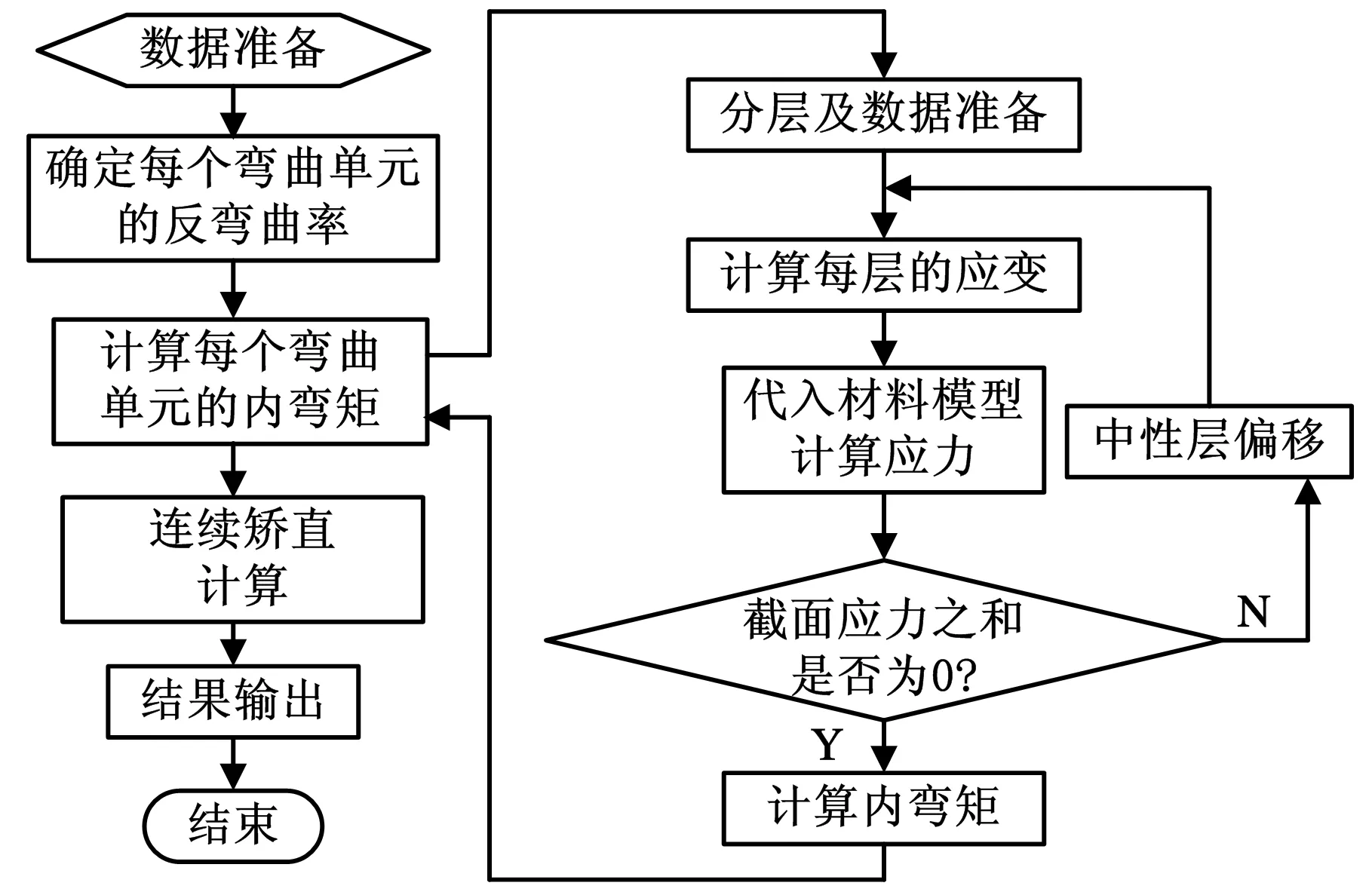
图2 分层算法内弯矩计算流程图

3 计算结果分析

计算板材的规格为：板材厚度h=25mm、板材宽度b=3000mm；计算材料性能按多线段近似应力应变曲线进行，为了简化说明问题，原始屈服强度取为350MPa，材料硬化线段斜率取0.1。同时，假定矫直前材料原始曲率C0=0，截面上应力分布均匀，均为0。

如图3所示，矫直过程中，反弯应变εw为矫直弯曲时，截面曲率从0变化到反弯曲率Cw所经历的应变，其在截面上的分布与其位置到中性层的距离成正比，呈线性变化。总的弯曲应变εΣ等于反弯应变εw与上弯曲单元残余应变εc之和。残余应变εc为总的弯曲应变εΣ与弹性应变εt之差；塑性应变εs为本弯曲单元的不能弹复的应变。

由于弹性应变εt等于σs/E(σs为屈服应力、E为弹性模量)，而σs与所在层的应变历史和本弯曲单元的总应变εΣ有关，呈非线性变化。因此，塑性应变εs在截面上表现为在距中性层一定距离内为0，在这个范围内材料只发生弹性变形，没有塑性应变，超过这个范围，塑性应变εs变化总体为从0开始逐步增大，但不是线性增大。塑性应变εs为弯曲单元实际经历的塑性变形，对塑性变形的计量可用于材料的不同应变历史下屈服应力的计算。

残余应变εc为板材在不受外力作用条件下，存在于板材内部的应变。残余应力σc为由于残余应变对应产生的应力，其值为σc=εcE。

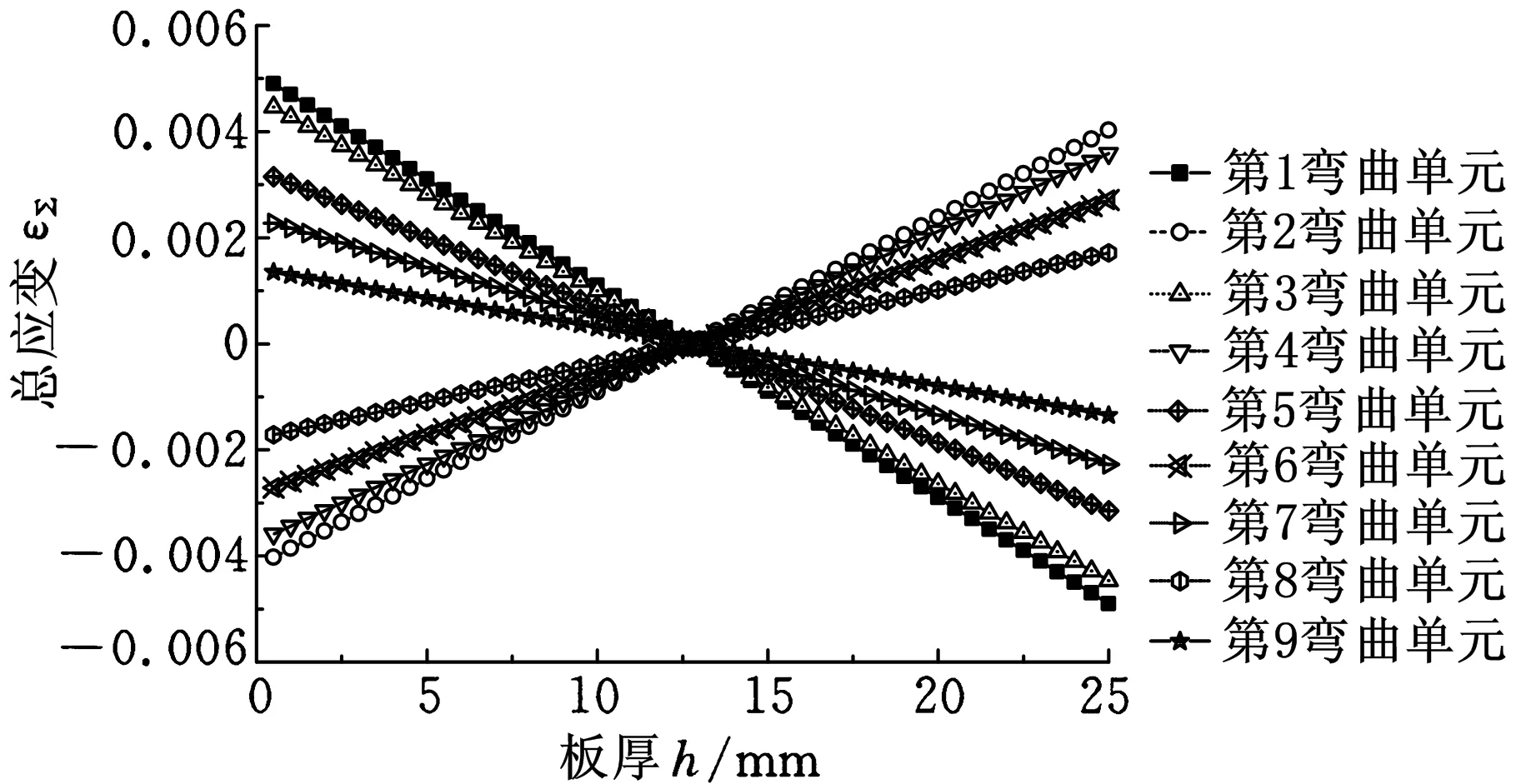
(a)总应变

(b)弯曲应力

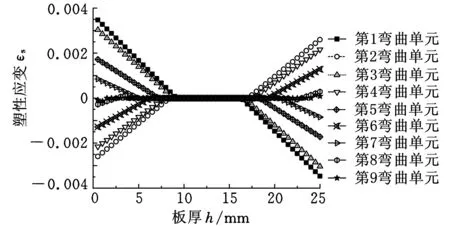
(c)塑性应变

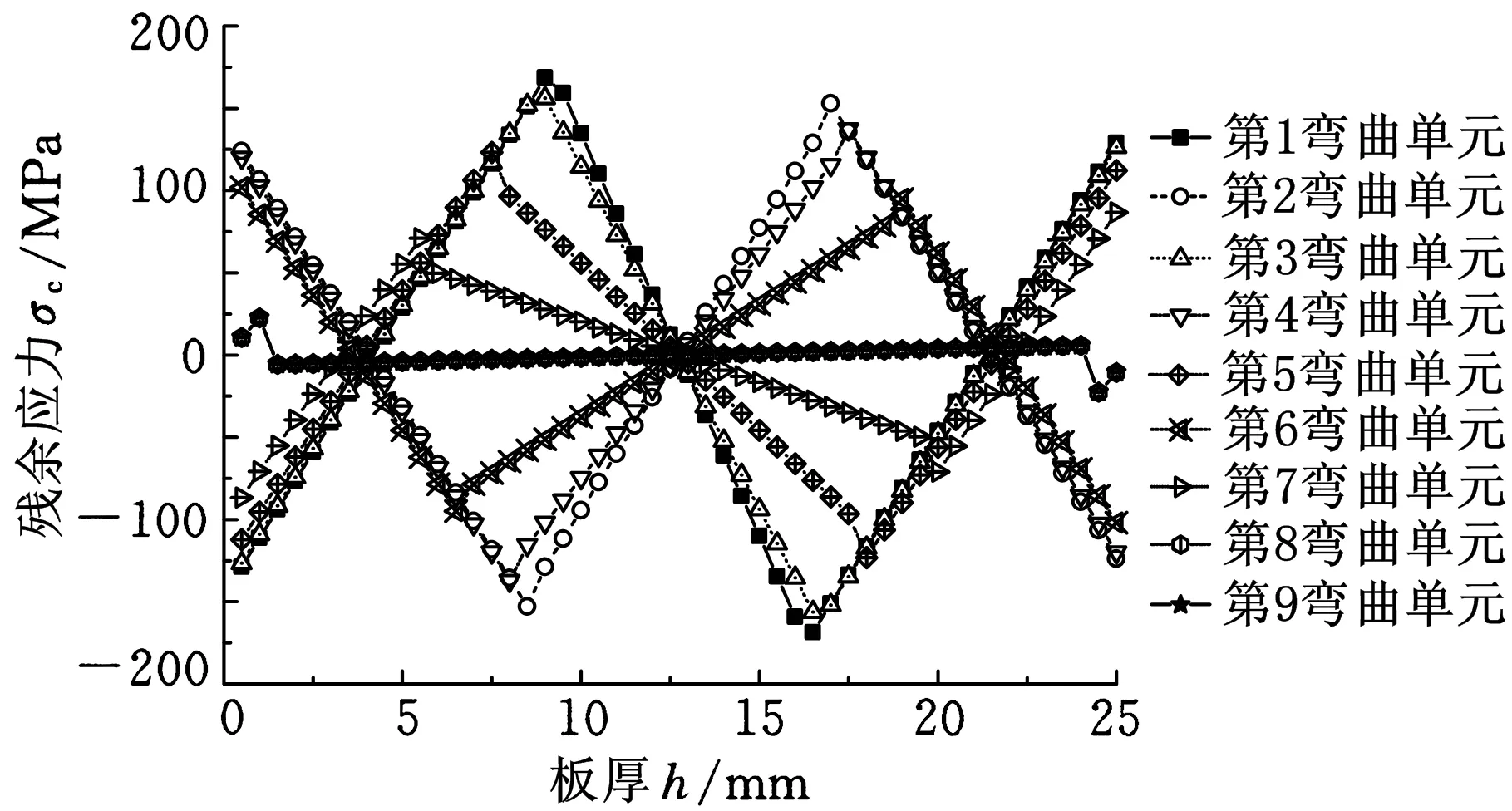
(d)残余应力图3 截面内各应力应变的分布

总弯曲应变εΣ等于反弯应变εw与上弯曲单元残余应变εc之和。随弯曲单元增加，反弯曲率逐步减小，总体上总的弯曲应变εΣ变小。在不考虑板材的原始曲率条件下，由于第1个弯曲单元的总的弯曲应变εΣ等于反弯应变εw，因此，总的弯曲应变εΣ在第2个弯曲单元处达到最大值。塑性区百分比在第2个弯曲单元处达到80%，随后随弯曲单元增加逐渐减小，在最后一个弯曲单元处，整个变形为弹性变形。

由于在计算过程中考虑到材料的应变历史，材料的变形抗力随应变的增大而增大，所以在单个弯曲单元的总弯曲应变减小的情况下，材料的变形抗力一直保持较小的增加，这样的计算方法所得到的力能参数值比采用其他方法所得的计算值偏大，尤其在高硬化指数的合金钢等材料矫直过程中，力能参数计算值较采用其他方法所得计算值大。

矫直过程中及矫直后的残余曲率的大小及分布一直是人们所关心的问题。本算法通过分层的独立变形运算和弯曲变形后板材各层中的曲率、应变、应力之间的关系，得到了截面上残余应力及其分布。在不考虑原始曲率的前提下，残余应力随弯曲单元序号的增加而减小，从第1弯曲单元残余应力最大为167MPa，变为矫直后的残余应力最大为28MPa；从其分布来看，在1～4弯曲单元，残余应力的最大值位于总的弯曲应变的弹性区向塑性区过渡的边界，在5～9弯曲单元，残余应力的最大值位于板材的表面。应该指出的是，由于板材原始曲率的存在，弯曲单元的应力应变并非相对中性层对称分布，从第1弯曲单元开始就存在明显的应力应变的中性层偏移，同时矫直后残余应力也为不对称分布，且残余应力值稍大于矫直前材料原始曲率C0=0时的残余应力值。

4 实际应用数据分析

利用液压伺服控制矫直实验平台对矫直过程中所记录的数据和算法计算结果进行验证。实验矫直平台型号为11-90/100-800，设计矫直能力为2000kN，矫直机综合刚度约为500kN/mm，矫直范围为2～6mm。板材来料不平度为10～15mm/m，采用平行矫直方案。实验矫直平台如图4所示。

图4 实验矫直平台

经过矫直，板材平直度均小于2mm/m；同时模型算法计算与实测值基本相符，模型算法计算值比实测矫直值偏小，原因可能为在板材辊式矫直过程中，由于矫直辊和板材的提前接触，使得实际板材弯曲量比理论值偏大，如表1所示。

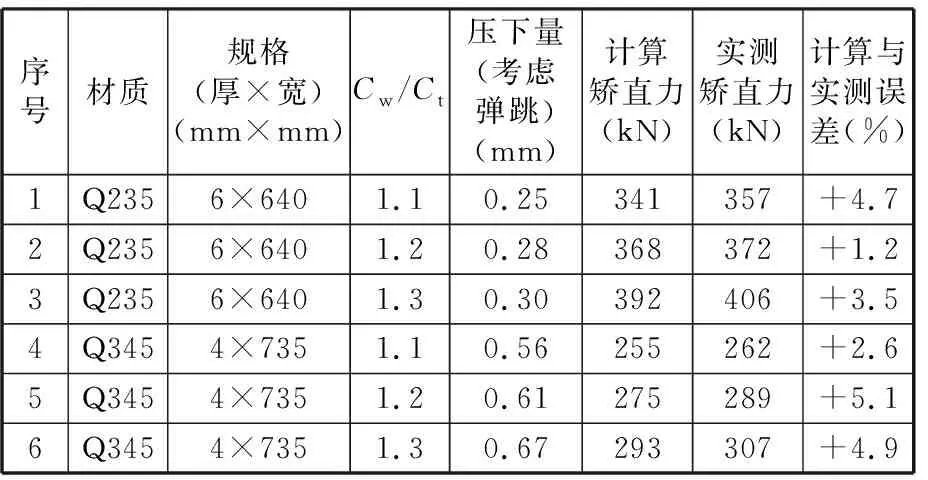
表1 记录数据与算法计算

5 结论

(1)弯曲过程分层算法是一种细化的弯曲变形解析算法，把材料模型和中性层偏移成功引入矫直计算过程，其算法结果与实验数据有较好的一致性。

(2)在计算过程中，由于考虑到材料的应变历史，所以在单个弯曲单元的总弯曲应变减小的情况下，材料的变形抗力一直保持增大，本计算方法所得力学性能参数值比其他方法计算值偏大。

(3)算法通过变形运算和变形过程中板材各层中曲率、应变应力之间的关系得到截面上残余应力。在不考虑原始曲率的前提下，残余应力随弯曲单元序号的增大而减小，从其分布来看，在1～4弯曲单元，残余应力的最大值位于弹性区向塑性区过渡处，在5～9弯曲单元，残余应力的最大值位于板材的表面。

[1] 阿高松男.「矯正工程の高精度化·高機能化」研究会を省みて[J].鉄と鋼,2009,14(11):731-731.

[2] 濱崎洋,志垣征聡,吉田総仁.確率的最適化手法によるテンションレベリンクエ程の信頼性設計[J].鉄と鋼,2009,14(1):740-746.

[3] Peter U.Flattening Straightening and Leveling[J].Metal Forming,2010,44(1):22-23.

[4] Philippaus V, Mailllard S.Modern Levelers for Advanced Plate Grades[J].Iron & Steel Review, 2009,52(10):144-148.

[5] 沈继刚,李宏图.现代辊式矫直技术在中厚板平直度控制中的应用[J].中厚板,2010,16(1):38-40.

[6] Grimm W, Korth J,Kohler W,et al.Ilsenburg Heavy-plate Mill:Modernisation of the Mill Stand Area and of the Hot-plate Leveller[J].Iron & Steel Review,2008,51(9):11-15.

[7] Bhooplapur P, Brammer M P, Steeper M J.Upgradingexisting Plate Mill for Higher Strength Product[J].Ironmaking & Steelmaking,2008,35(7):491-495.

[8] 王效岗,黄庆学,马勤.中厚板的横向波浪矫直研究[J].中国机械工程,2009,20(1):95-99.