沿任意倾斜面的机器人力/位置控制方法研究

李正义 唐小琦 熊 烁 叶伯生

华中科技大学国家数控系统工程技术研究中心，武汉， 430074

0 引言

机器人与未知环境间的力/位置控制主要研究减小未知环境的几何参数和动力学参数(惯量、阻尼、刚度)对控制系统性能的影响及如何提高机器人力/位置控制的自适应能力等，其中关于机器人与任意倾斜面间的力/位置控制以其环境模型相对简单受到众多学者青睐。文献[1-2]给出了基于机器人关节角位移、角速度的倾斜面法向矢量在线自适应计算公式，但算法收敛较慢；文献[3-4]根据机器人关节角位移和机器人末端接触力设计了能同时进行斜面法向方向估计和实现力/位置控制的算法，接触面切向速度恒定，但算法复杂、难以工程实现；文献[5]结合力觉、视觉和位移传感器实现了任意斜面上的机器人力/位置控制；文献[6]对比研究了未知环境参数(阻尼、刚度)估计的几种方法，指出各种方法应用于机器人力/位置控制的优缺点；文献[7]提出利用递归最小二乘(recursive least squares,RLS)算法估计环境阻尼和刚度参数，并设计了基于神经网络的PI控制器实时补偿环境参数估计误差。总之，机器人与环境间的力/位置控制算法较复杂、难以工程实现，目前大都处于仿真阶段，设计易于实现的机器人与环境间的力/位置控制方案有着重要意义。

本文设计了机器人自适应阻抗控制方法以实现机器人末端执行器沿任意倾斜面的力/位置控制，主要内容包括利用机器人末端与接触面碰撞接触激发环境的动态特性，由RLS算法估计环境的阻尼、刚度；接触稳定后，根据接触力矩调整机器人末端姿态到期望值；在机器人末端沿斜面滑动过程中，由于机器人末端位移相对值变化小，接触力测量噪声大，设计了基于位移和接触力反馈的模糊控制器以实时修正阻抗控制模型的阻尼和刚度参数，使其满足环境的阻尼、刚度变化和补偿估计误差的需要。

1 机器人阻抗控制模型

Hogan[8]提出了机器人阻抗控制方法，该方法通过将机器人末端力/位置控制等效为“弹簧-质量-阻尼”模型，建立了机器人末端位移与接触力的关系，并通过任意调节惯性、阻尼、刚度参数来调整机器人末端位置与接触力的关系，阻抗控制克服了机器人力/位置混合控制中力控制与位置控制频繁切换的缺点。机器人阻抗控制理想模型为[7]

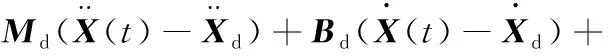
(1)

E(t)=Fd-Fe(t)

式中，X(t)为机器人末端当前位置；Xd为机器人末端期望位置；X(t)和Xd的一阶、二阶导数表示对应的速度、加速度；Md为机器人阻抗模型理想惯性矩阵；Bd为阻抗模型理想阻尼矩阵；Kd为阻抗模型理想刚度矩阵(为实现解耦控制，Bd、Kd和Md都取为l×l正定对角矩阵，l为机器人工作空间维数)；Fd为机器人末端期望接触力；Fe(t)为实际接触力。

机器人阻抗控制就是通过调整参数Md、Bd和Kd实现机器人末端期望的位移和接触力控制。机器人阻抗控制中的环境常近似为“弹簧-阻尼”系统[7]：

(2)

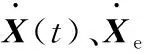
2 环境参数对机器人阻抗控制的影响

机器人阻抗控制应用于机器人与环境间力/位置控制时，环境参数未知或变化使控制系统的动静态性能变差，分析环境的刚度、阻尼对机器人与环境间力/位置控制性能的影响是应用机器人阻抗控制的基础[6]。

2.1 稳定误差影响

当机器人末端与环境接触并处于稳定状态时，对于机器人阻抗控制模型(式(1))有

Fe-Fd=Kd(X-Xd)

对于环境模型(式(2))，则有

Fe=Ke(X-Xe)

为实现Fd=Fe，要求

Xd=Xe+Fd/Ke

定义机器人实际控制目标轨迹Xr为“参考轨迹”，取

Xr=Xe+Fd/Ke

用Xr替换式(1)中的Xd，得

易知当时间t→∞时，机器人末端位移：

X(t)→Xr=Xe+Fd/Ke

机器人末端与环境间接触力：

F(t)=Ke(X-Xe)→Fd

即同时实现了机器人末端期望的接触力和位置控制，但实际应用机器人阻抗控制时，Ke的值大多是未知的或是变化的，需在线计算Ke。

2.2 动态性能影响

将式(2)代入式(1)并令Xe=Xd，将机器人与环境间相互作用等效为二阶系统，此二阶系统的阻尼系数ξ和无阻尼振荡角频率wn满足[7]：

其中，md、kd、bd、ke和be分别为矩阵Md、Kd、Bd、Ke和Be中对应的元素，表示某一方向上的等效质量、刚度和阻尼。由于wn和ξ决定了二阶系统动态性能，因此，当环境参数(ke,be)变化导致(wn,ξ)变化时，为保持设定的机器人与环境间力/位置控制系统动态性能不变，阻抗控制模型参数(md,kd,bd)必须根据环境变化实时调整。调整的方法一种是实时测量或根据环境模型计算出(ke,be)的值，修改(md,kd,bd)以补偿环境的变化；另一种方法是设计智能控制器，根据机器人末端位移和接触力反馈实时调整(md,kd,bd)，降低环境变化对系统动态性能的影响。本文设计的力/位置控制方法在机器人与环境作用不同阶段分别采用这两种方法提高系统对环境参数未知或变化的自适应能力。

3 沿倾斜面的机器人力/位置控制设计

机器人沿倾斜面的力/位置控制主要是机器人末端沿接触面法向方向的接触力跟踪控制和沿接触面切向方向的轨迹控制，实际任务(抛光、打磨)中一般给定接触面法向期望接触力、机器人末端姿态与倾斜面间的夹角和沿接触面切向的轨迹，因此，应用机器人阻抗控制实现沿倾斜面的力/位置控制时，需解决机器人末端姿态、环境阻尼、刚度未知的问题。本文在机器人末端与环境碰撞接触过程中利用RLS算法估计环境参数(Be,Ke)，接触稳定后由接触力矩计算出机器人末端姿态调整旋转矩阵；在机器人末端沿倾斜面滑动阶段，设计模糊控制器实时调整系统参数(Bd,Kd)，实现机器人力/位置控制对环境参数(Be,Ke)变化的自适应性。

3.1 环境参数(Be,Ke)初值估计

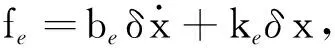
式中，z为复变量；T为采样时间。

对应差分方程为

k=1,2,…

将其改写为

Y(k)=φT(k)θ(k)

θ(k)=[A1(k)A2(k)]T

φ(k)=[δx(k) δx(k-1)]T

Y(k)=fe(k)+fe(k-1)

则由RLS算法得θ(k)的计算式如下：

θ(k)=θ(k-1)+G(k)(Y(k)-φT(k)θ(k-1))

其中,G(k)为增益因子；λ为遗忘因子，一般取0.9；P(k)为参数估计协方差矩阵，其递归计算式为

在迭代计算过程中，当θ(k)值变化小于设定阈值时，认为θ(k)值是稳定的，得到θ(k)值后由a1、a2的计算式得(be,ke)估计值分别为

依照类似的方法可得其他方向上的(be,ke)参数，若为提高(be,ke)估计的准确性，可让碰撞接触过程中系统处于欠阻尼状态[6]，获得笛卡儿空间三个相互垂直方向上的(be,ke)后，组合即为环境的阻尼和刚度矩阵(Be,Ke)。

3.2 机器人末端姿态调整

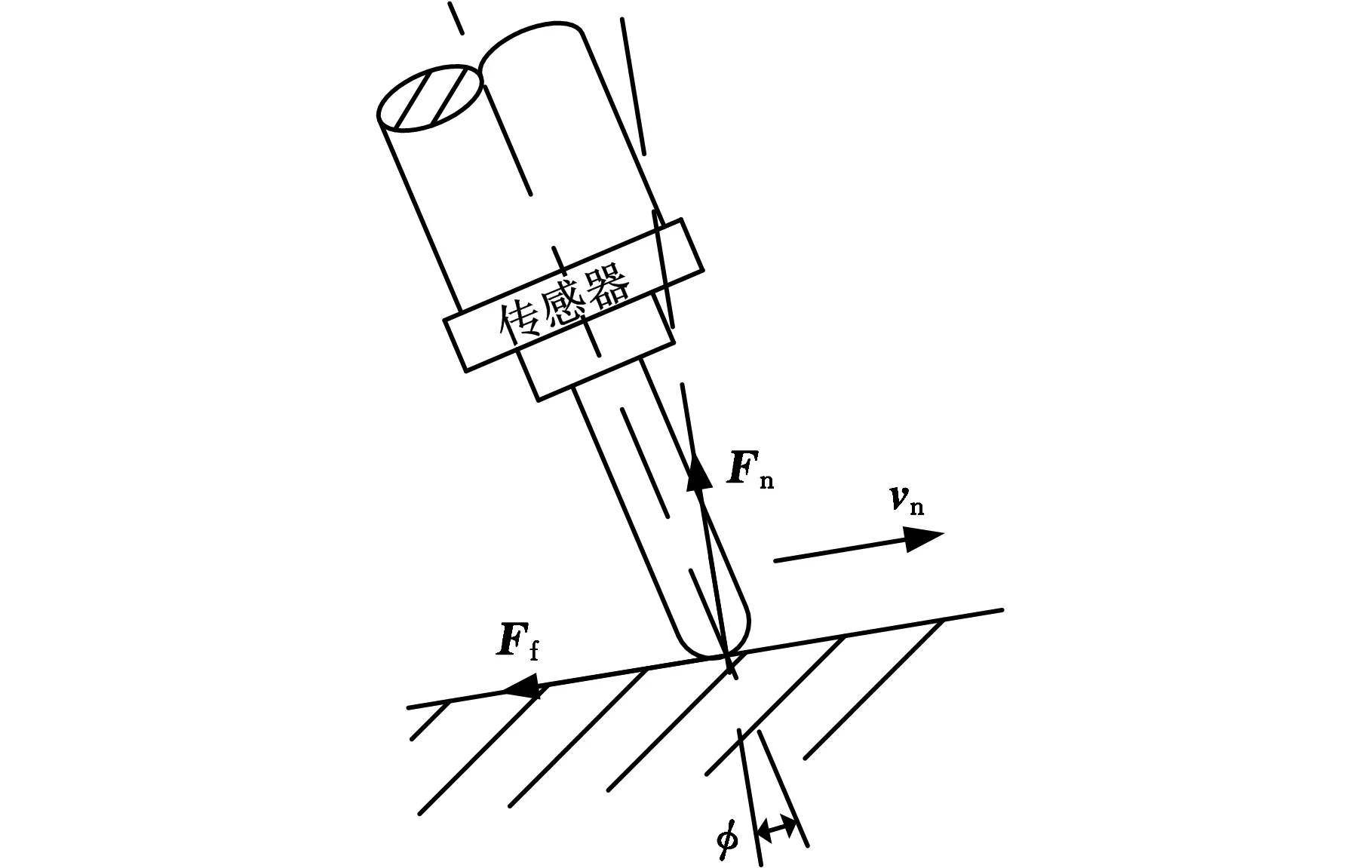
图1 机器人与斜面接触示意图

机器人末端受力如图1所示，vn为机器人末端速度，只要在初始接触时调整好机器人末端相对倾斜面的姿态，以后机器人末端沿倾斜面滑动时可不用调整姿态，因此，本文采用在机器人末端与倾斜面初始稳定接触时根据接触力矩调整机器人末端姿态。Fn为倾斜面法向压力，Ff为摩擦力，由于机器人末端与倾斜面初始稳定接触时沿倾斜面运动趋势较弱，可忽略Ff，则在当前姿态下，Fn在机器人末端产生力矩为Mn(k)，设机器人末端在期望姿态下Fn可产生力矩Md，定义em(k)=Md-Mn(k)，当前机器人末端姿态调整旋转矩阵在机器人工具坐标系下为TR(k+1)(力传感器坐标系与工具坐标系T重合)[9]：

k=0,1,2,…

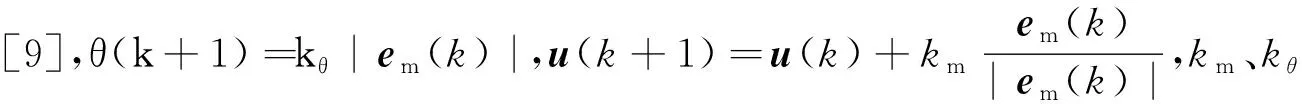
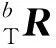
3.3 模糊控制应用于机器人阻抗控制

根据3.2节给出的方法，当机器人经过姿态调整达到期望姿态后，可计算出接触面法向方向单位矢量N，则机器人末端沿N方向压力Fn=FN，F为接触合力，定义fn=‖Fn‖，fd=‖Fd‖，在阻抗控制式(式(1))中取Md=mdIl×l、Bd=bdIl×l、Kd=kdIl×l，其中，Il×l为单位矩阵，则得单一方向(N方向且与操作空间坐标系中某一坐标轴重合)上机器人阻抗控制满足：

(3)

其中，ex=x-xd，ef=fn-fd分别表示N方向上机器人末端的位移、接触力误差；md、bd和kd分别表示系统在N方向上期望的惯性参数、阻尼和刚度值；对于任意方向上的阻抗控制，Md、Bd和Kd对角线上元素分别表示系统在操作空间各个自由度方向上的惯性参数、阻尼和刚度，即根据6个类似式(3)的求解得到机器人沿任意方向上的力/位置控制参数。在机器人末端沿接触面滑动过程中，环境的阻尼、刚度会变化，且机器人在不同姿态时，末端等效阻尼、刚度也不同，因此，需实时调整阻抗模型参数以适应环境变化，机器人受力控制时，运动速度慢，仅需考虑调整参数(bd,kd)。

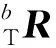
(4)

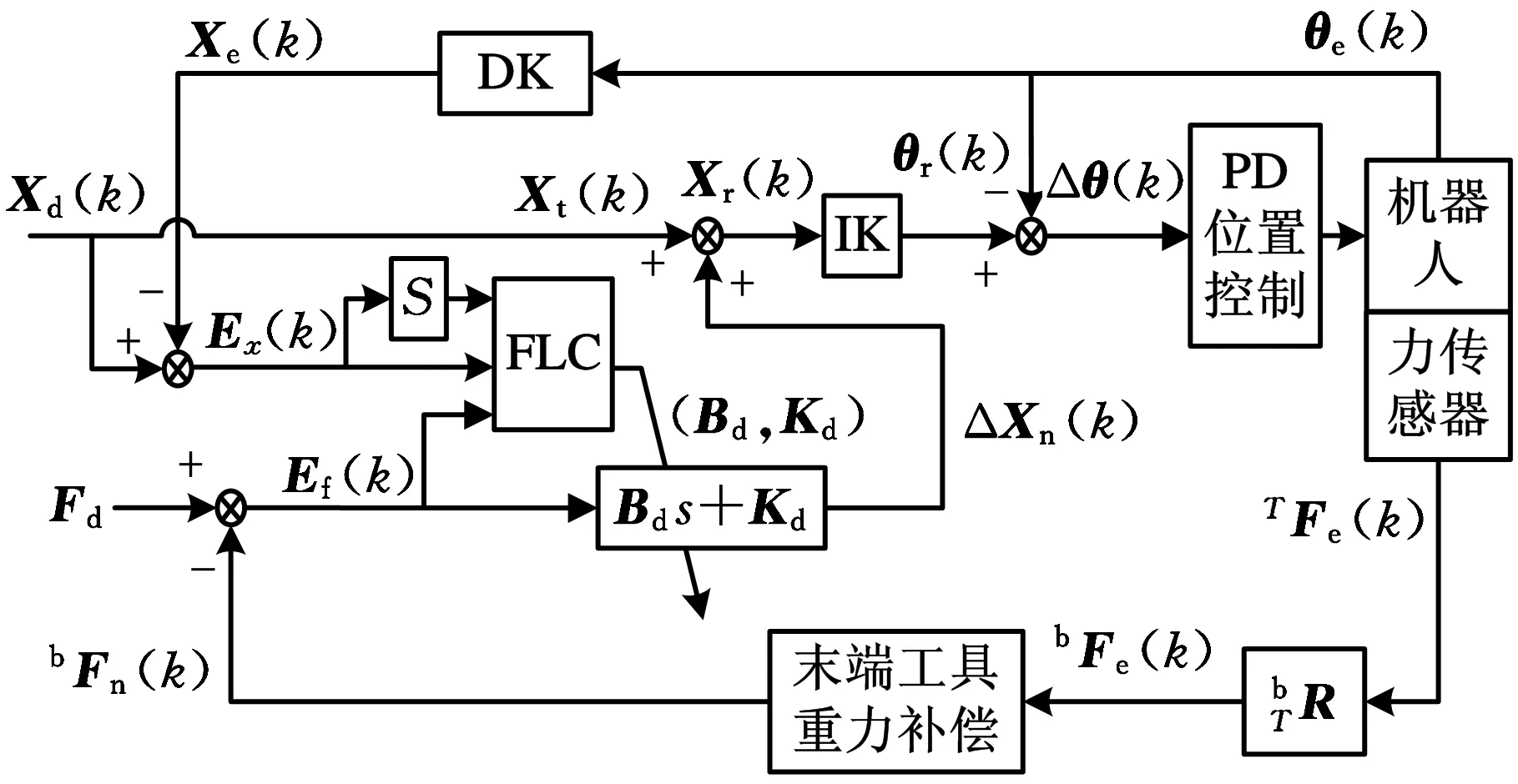
图2 机器人力/位置阻抗控制框图

系统刚度参数调整表达式为

(5)

k=0,1,2,…

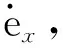
(6)

t=1,2,…

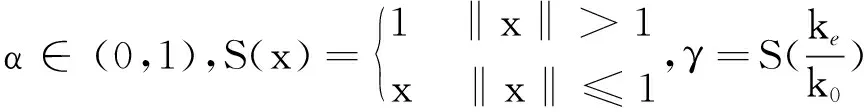
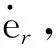
4 实验及结果

图3 沿斜面力/位置控制实验图

利用实验室改造的5自由度工业机器人设计实验，控制系统硬件平台为武汉华中数控HNC-210B控制器和HSV-18伺服驱动，软件平台基于DOS系统，位置控制周期为4ms，在机器人末端安装有ATI Delta力传感器(精度达0.1N，采样频率为7kHz)和作为探针的铝制光滑圆棒。实验现场如图3所示，将具有一定弹性、表面光滑的木板(表面为平面)以任意倾角(取约70°)固定于墙壁上，要求控制探针始终以期望姿态与木板平面接触并沿木板平面滑动，为便于计算，期望姿态取探针与木板平面垂直，期望接触力沿木板法向方向，大小为2N，木板平面切向运动则由控制面板上方向键控制。具体实验时，先将机器人末端运动到与木板平面接近的位置，然后启动接触力控制功能，由于当前接触力小于期望值(2N)，机器人末端向木板运动直到接触力稳定为2N，在探针与木板接触过程中采用RLS算法估计环境参数(be,ke)，接触稳定后根据测量的接触力矩值(期望姿态下的接触力矩理论值为0)调整探针姿态，使探针与木板平面垂直，同时，根据各个关节角位移计算出当前接触点在机器人基坐标系下的坐标，最后由手动操作控制面板上的方向键控制探针沿木板平面滑动：相对基坐标系先沿-x方向运动再沿+x、-z两方向同时运动，系统速度设定为20mm/s。

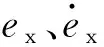
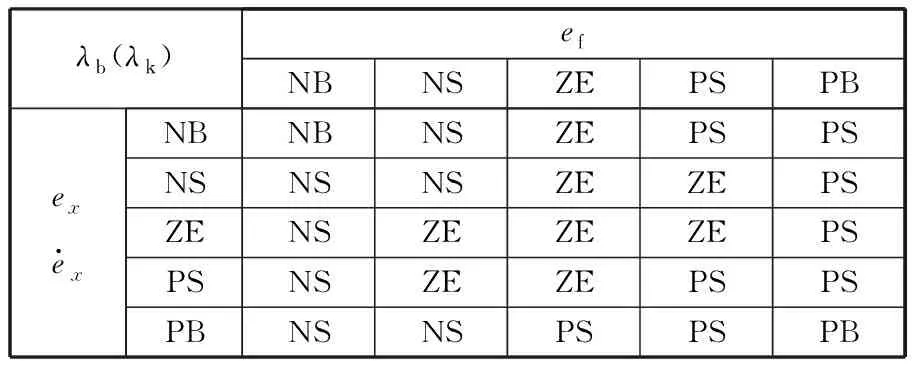
表1 模糊控制规则表(α=0.5)

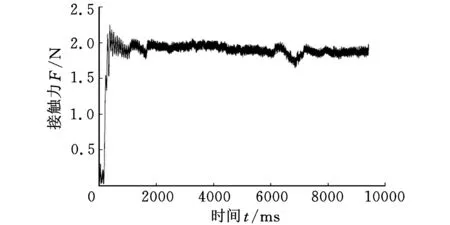
图4 倾斜面法向接触力

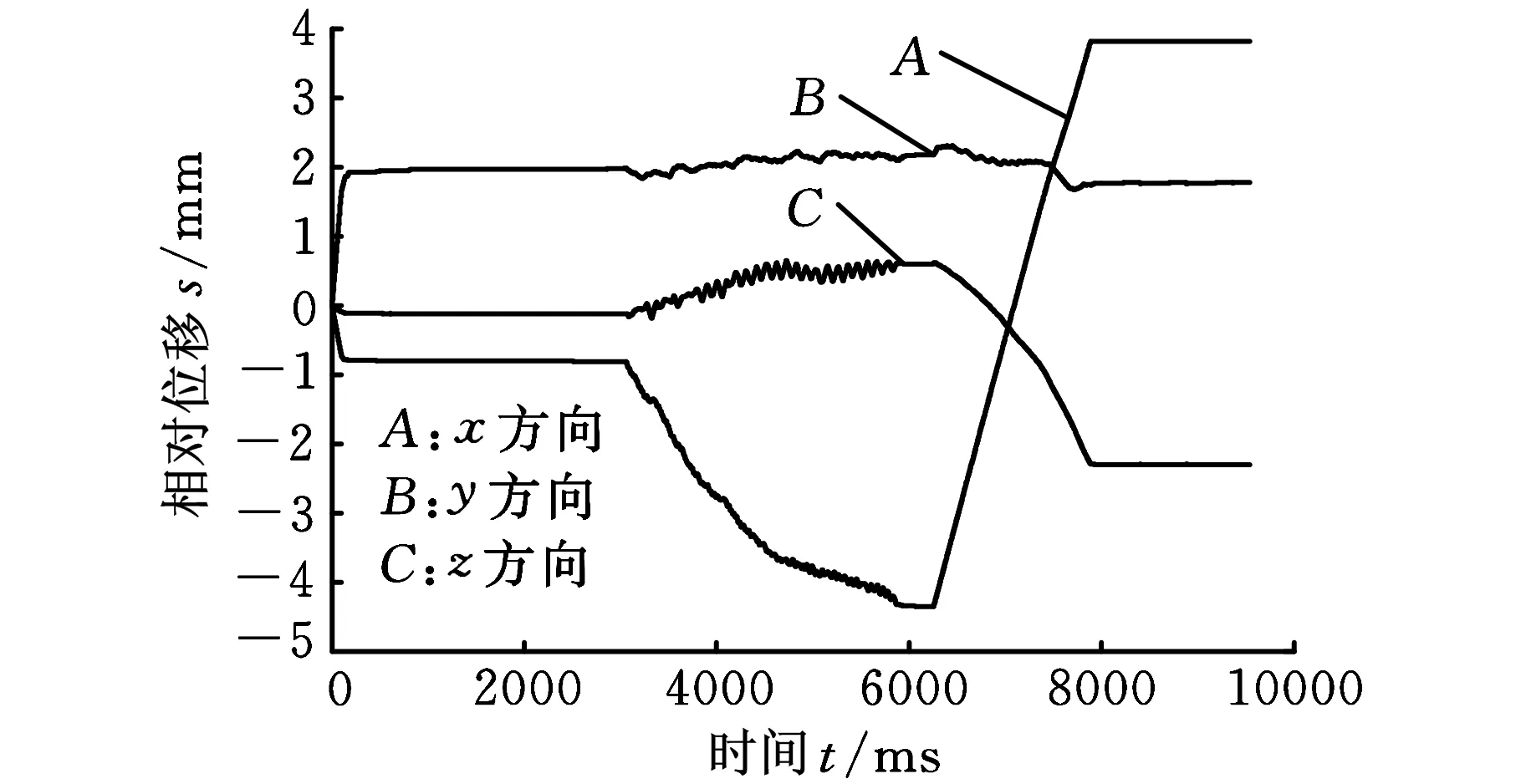
图5 机器人末端(探针)在基坐标系下位移

5 结语

本文设计了自适应阻抗控制实现了机器人沿任意倾斜面的力/位置控制，解决了倾斜面法向方向未知以及环境阻尼、刚度未知影响机器人力/位置控制性能的问题，具有编程简单易于实现的优点。为减少接触面摩擦力对机器人末端姿态调整的影响，在机器人与环境初始接触稳定时，根据当前姿态下接触力矩调整机器人末端到期望姿态；在机器人沿倾斜面滑动过程中，设计具有规则自调整的模糊控制器，根据机器人末端位移误差及其变化率和接触力误差实时调整系统的阻尼、刚度参数，以减小环境参数未知对机器人阻抗控制性能的影响。

[1] Karayiannidis Y, Doulgeri Z. An Adaptive Law for Slope Identification and Force/Position Regulation Using Motion Variables[C]//IEEE International Conference on Robotics and Automation. Orlando: IEEE, 2006: 3538-3543.

[2] Doulgeri Z, Karayiannidis Y. Force/position Regulation for a Robot in Compliant Contact Using Adaptive Surface Slope Identification[J]. IEEE Trans. On Automatic Control, 2008, 53(9):2116-2122.

[3] Karayiannidis Y, Doulgeri Z. Adaptive Control for Frictional Robot Contact Tasks on Uncertain Surface Slopes[C]//16th Mediterranean Conference on Control and Automation. Ajaccio: IEEE, 2008:932-937.

[4] Karayiannidis Y, Doulgeri Z. Robot/Force Position Tracking on a Surface of Unknown Orientation[C]//European Robotics Symposium.Heidelberg: Springer,2008:253-262.

[5] Olsson T, Bengtsson J, Johansson R. Force Control and Visual Servoing Using Planar Surface Identification[C]//IEEE International Conference on Robotics and Automation.Washington:IEEE,2002:4211- 4216.

[6] Erickson D, Weber M, Sharf I. Contact Stiffness and Damping Estimation for Robotic Systems[J]. Int. J. Robot. Res.,2003,22(1):41-57.

[7] Mallapragada V, Erol D, Sarkar N. A New Method of Force Control for Unknown Environments[J]. International Journal of Advanced Robotic Systems,2006,4(3):4509-4514.

[8] Hogan N. Impedance Control: an Approach to Manipulation: Part Ⅰ- Theory, Part Ⅱ-Implementation, Part Ⅲ-Application[J] . ASME Journal of Dynamic System, Measurement and Control,1985,107(1):1-24.

[9] Calvelli T, Bona B. How to Cope with a Closed Industrial Robot Control: a Practical Implementation for a 6-dof Articulated Robot[C]//SYROCO 2003. Wroclaw: IEEE,2003:637-642.

[10] Hu Zhongxu, Bicker R, Marshall C. Position/force Control of Manipulator Based on Force Measurement and Its Application to Gear Deburring[J]. Journal of Intelligent & Fuzzy Systems,2003,14:215-223.