参数曲线柔性加减速前瞻控制算法

王海涛 赵东标 陆永华 刘 凯

南京航空航天大学，南京，210016

0 引言

目前，参数曲线(曲面)广泛应用于航空、模具等制造领域中，复杂曲线、曲面的造型技术发展迅猛。对于复杂参数曲线的插补，传统数控系统在规划复杂参数曲线加工轨迹时，必须将曲线加工刀具路径处理成大量离散的直线段来编制数控加工程序[1-2]，此种处理方法会导致编程复杂，效率低，造成数控代码在传输过程中误码率上升，加工状态不稳定。为了解决这一问题，很多学者采用泰勒展开式的方法进行直接插补[3]，此方法大大简化了编程，提高了效率，但是由于速度有波动而很难保证精度。Yong等[4]综合了系统允许轮廓误差条件下进给速度的变化情况，采用二分法设计插补中加减速控制方法，保证了插补时加速度在系统允许范围内，缺点在于这种方法只针对特定的加减速特性曲线，不能适应曲线复杂多变的特性。Nam等[5]提出了加加速度限制条件下的进给速度的加减速变化控制方法，当加速度、加加速度超过系统性能的允许范围时，采用均匀变化的加速度曲线来控制进给速度的突变，减少了速度的突变对系统性能的影响，但有些情况下加工误差仍然难以满足精度要求。Du等[6]提出了一种自适应的前瞻插补算法，在对速度进行自适应控制的同时进行前瞻控制，找出速度变化超过允许范围的敏感点，提前进行加减速规划，尽量避免速度变化过大对机床产生冲击，但是这种方法没有对加加速度进行控制。曹宇男等[7]设计了一种基于S形加减速的前瞻控制算法，算法中设定了最大前瞻段数，并根据实际插补轨迹的几何特性实现了加减速的控制。但是在对复杂曲线进行加减速控制时，其前瞻距离的确定有一定的困难。

本文在以上研究基础上，提出了一种实时参数曲线插补的柔性加减速前瞻算法，首先根据插补精度进行速度自适应控制，通过将曲线划分为曲率上升点和曲率下降点来对曲线进行前瞻处理，在加减速过程中，在使用S形柔性加减速算法的同时，在曲率频繁变化处对加减速进行重新规划，然后通过自行开发的数控系统验证了算法的可行性。

1 参数曲线的自适应插补

参数曲线的方程可以表示成如下形式[8](以三维曲线为例，u为参变量)：

C(u)=(x(u),y(u),z(u))

(1)

其中，u∈[0,1]，通过泰勒展开，经过变化，可以近似得到插补中参变量的计算方程：

(2)

式中，T为插补周期；v为进给速度。

在插补过程中，限定弓高误差为δ，限定系统的最大进给速度为vmax，插补点的实际弓高误差为ρi，当遇到大曲率点，以vmax加工超过限定弓高误差时，就需要进行减速，则相应插补点的进给速度V(ui)为

(3)

因此，进给速度V(ui)就随δ和ρi的变化自适应地调整，调整规则如下：

(4)

但是对于曲率急剧变化的点，按照此种规则调整就会引起速度的急剧变化，给机床带来冲击。

2 参数曲线柔性加减速前瞻控制算法

为了解决上述问题，就需要在曲率变化点对速度进行前瞻控制，使进给速度在满足弓高误差的同时满足柔性加减速的要求。

2.1 柔性加减速的速度规划

S形加减速方法作为一种数控系统插补的柔性加减速方法，能够有效地避免速度和加速度的突变，提高数控系统的加工精度，但是S形加减速算法比较复杂，特别对于一些变化复杂的曲线，频繁地加减速会加大系统的计算量，因此，本文使用三角函数加减速方法对曲线上频繁加减速区域进行规划。

对于频繁加减速区域的速度规划有以下两种情况：加速+减速→加速，如图1所示；加速+减速→减速，如图2所示。

图1 参数曲线前瞻加速规划前

图2 参数曲线前瞻减速规划前

2.1.1加速+减速→加速情况

在曲率频繁变化处使用S形加减速方法规划速度曲线如图1所示，此时速度频繁变化，S形加减速方法计算复杂，容易加重系统负荷。如果采用三角函数的加减速方法，如图3所示，则可以大大简化加减速计算，其具体方法如下。

图3 参数曲线前瞻加速规划后

在曲线的规划中采用的三角函数曲线为

(5)

分析整个规划过程，其速度变化方程为

(6)

式中，ta_act为规划后实际加速时间。

则其加速度、加加速度为

(7)

(8)

在三角函数加速过程中，其加加速度和加速度的最大值为

(9)

(10)

由于速度规划前和速度规划后两点间的距离是不变的，且其速度规划两点间的距离Li可由规划前的加减速方程得到，即

(11)

则可得到加速时间ta_act：

(12)

2.1.2加速+减速→减速情况

在加速+减速→减速的规划中，使用的三角函数的减速特性曲线为

(13)

前瞻减速规划前参数曲线如图2所示，规划后如图4所示。

图4 参数曲线前瞻减速规划后

2.2 参数曲线柔性加减速的前瞻控制策略

所谓前瞻，就是对要插补的参数曲线进行预插补处理，通过预插补找出插补路径上的速度敏感点及其对应的进给速度以及插补距离，然后对进给速度进行规划，以便提早进行加减速处理，以满足误差及机床的性能要求。

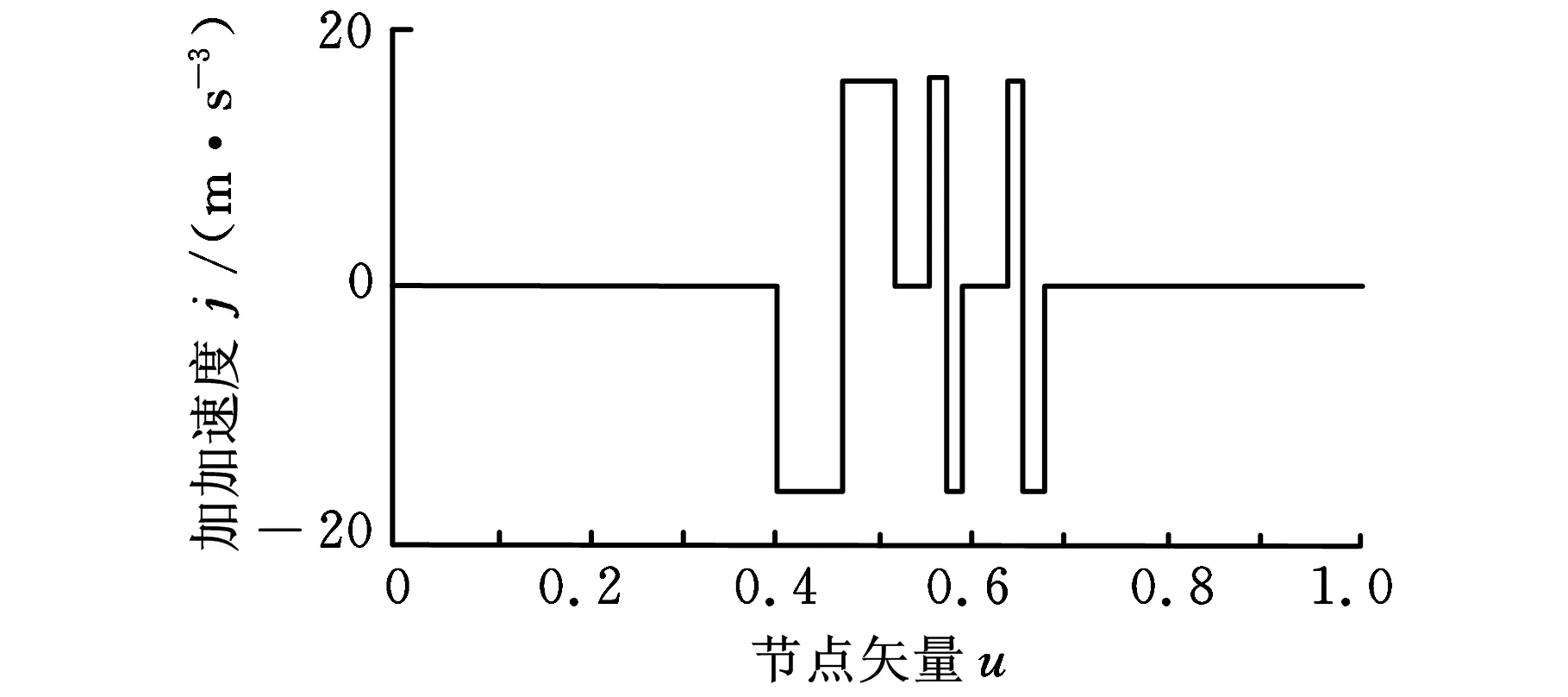
在前瞻的插补预处理中，将曲线分为两种情况——曲率上升和曲率下降。曲率上升时说明在插补过程中要遇到拐点，需要进行减速处理，而曲率下降说明从拐点开始速度开始增大。因此将前瞻的预插补分为曲率上升模块和曲率下降模块。当前瞻开始时的速度vstart

(1)前瞻中曲率上升模块。当前瞻的初始速度vstart=vmax时，说明此时预插补的加工速度处于最大阶段，在预插补的过程中有可能出现曲率上升阶段，当曲率上升时，弓高误差变大，进给速度就要减小，进入减速阶段；另外也有可能在预插补过程中曲线形状不发生大的变化，进给速度也不发生变化，因此，对于此种情况其前瞻预读距离也根据曲线形状动态变化，如果加工速度不发生变化，则预读距离为从vmax减速到0所需要的距离，如果此时遇到拐点，曲率发生变化，则前瞻距离预读至整个拐点的曲率最大处。在前瞻过程中首先通过预插补分析各个插补点，以最大加工速度vmax来计算各个插补点的位置，然后求出其弓高误差，并且比较所得弓高误差与系统允许最大弓高误差δ的差值，如果在允许范围内，则继续比较下一个插补点；否则，根据式(4)确定此点的最大加工速度，并且分析此点是否仍旧处于曲率增大的范围，如果是，则继续分析比较下一个插补点，直到找到曲率最大点，并且记录此点的位置ui及最大的约束速度vend。如果在前瞻预读的从vmax减速到0所需要的距离中，没有出现曲率波动点，则记录最后前瞻插补点ui。其具体前瞻过程如图5所示。

图5 参数曲线柔性加减速曲率上升前瞻模块

(2)前瞻中的曲率下降模块。当前瞻的初始速度vstart

首先以速度v=vmax预插补并分析各个插补点的弓高误差，因为此时处于曲率下降的阶段，所以弓高误差应该是一个变小的过程，所以，通过计算可以找到一个v=vmax且满足弓高误差(即ρi<δ)的插补点，这样就可以把曲率下降的加工路径的速度规划出来了。但是当插补路径变化复杂，需要频繁加减速的时候，有时弓高误差约束速度还未达到vmax，可能又会有新的拐点出现，曲率就会转而变大。如果出现这种情况，则找到新的敏感点的最大曲率处，表明此段前瞻路径是速度频繁加减速区域，设定Fv_plan=1，表明此路径需要根据上文使用三角函数加减速方法对速度进行规划。因此，其前瞻距离的大小随曲线曲率的变化自适应改变，具体的前瞻过程如图6所示。图5和图6中，L为前瞻预读距离，本文中选取S形加减速从vmax减到0的距离；uend为前瞻结束后寻找到的速度敏感点，如果在此段前瞻距离上没有拐点，则该点就是前瞻距离的最后插补点；vend为满足弓高误差的速度敏感点的速度；vi为预插补点上的进给速度；s为实际前瞻的距离；l为每个插补周期内的位移量；ρi为预插补点上的弓高误差；ρmax为记录的前瞻预插补过程中的最大曲率；Fv_plan为速度重新规划标志，当需要对频繁加减速区域进行重新速度规划时，Fv_plan=1，否则Fv_plan=0。

图6 参数曲线柔性加减速曲率下降前瞻模块

这样，就可以得到整个前瞻路径上的曲率变化的特征，并且据此来对速度进行规划。

3 参数曲线柔性加减速前瞻控制算法仿真与实验

为了验证算法的可行性，仿真加工一段三次有理样条曲线(图7)。插补周期设为4ms，最大速度vmax=100mm/s，最大加速度amax=1m/s2,最大加加速度jmax=20m/s3,曲线的控制顶点数据如表1所示。

图7 加工的NURBS曲线

表1 加工路径数据点

如图8所示，采用自适应插补方法能将弓高误差控制在允许范围之内，但是为了控制误差，未使用前瞻插补算法和使用前瞻插补算法，速度的变化是不相同的。在未使用前瞻插补算法时，不能提前知道曲线的拐点，因此无法使用S形加减速算法，其速度变化如图9a所示，当遇到高曲率点时其速度突然变小，因此带来了很大的加速度变化，如图10a所示，其最大加速度竟然接近10m/s2，整整超出了限定值的9倍多，这必然会给机床带来很大冲击。

图8 参数曲线加减速弓高误差变化曲线

通过图9b使用前瞻算法的速度变化图、图10b使用前瞻算法的加速度变化图和图11可以看出，使用具有前瞻功能的插补算法，在良好控制弓高误差的同时，速度、加速度、加加速度都在限定范围内，满足了机床性能要求。

(a)未用前瞻算法(b)使用前瞻算法图9 参数曲线加减速速度变化曲线

(a)未用前瞻算法的加速度曲线(b)使用前瞻算法的加速度曲线图10 参数曲线加减速加速度变化曲线

图11 参数曲线加减速加加速度变化曲线

在加工过程中，使用自主研发的基于RT-linux的数控系统，采用R2.5mm的高速钢球头铣刀，在此相同的加工参数下，图12a为未采用前瞻控制算法得到的加工零件图，图12b为采用前瞻控制算法得到的加工零件图。选取其中两处进行放大比较，如图13、图14所示。

(a)未采用前瞻控制算法(b)采用前瞻控制算法图12 加工试件

(a)未采用前瞻控制算法(b)采用前瞻控制算法图13 试件1处局部放大图

(a)未采用前瞻控制算法(b)采用前瞻控制算法图14 试件2处局部放大图

图13a和图14a所示为使用传统的加减速方法加工的零件。可以看出其加工轨迹上有加工缺陷，表面比较粗糙，并且有明显接刀痕。而采用前瞻控制算法加工获得的试件如图13b和图14b所示，相比传统方法而言，使用前瞻控制算法加工获得的试件，其加工质量提高了，加工缺陷减少了，加工表面也更加光滑了。

4 结语

本文提出了一种参数曲线的S形加减速和三角函数加减速的混合型柔性加减速前瞻控制方法，在前瞻控制中以S形加减速为基础，并在曲率频繁变化处使用三角函数的加减速方法来简化计算。在前瞻过程中，采用将路径根据曲率变化分为曲率上升段和曲率下降段的方法来对前瞻路径进行划分，这样不仅仅能适应参数曲线的复杂变化，而且降低了计算的复杂性，满足了数控系统的实时性要求。通过仿真和实验可知，此种前瞻方法提高了加工质量，取得了较为理想的结果。

[1] 苟琪.MasterCAM五轴加工方法[M]. 北京: 机械工业出版社, 2005.

[2] 吴光琳. 组合曲面实时插补关键技术研究[D]. 上海: 上海交通大学, 2000.

[3] Shpitalni M, Koren Y, Lob C C. Realtime Curve Interpolators[J]. Computer-Aided Design, 1994, 26(11): 832-838.

[4] Yong T, Narayanasami R. A Parametric Interpolation with Confined Chord Error Acceleration and Deceleration for NC Machining[J]. Computer-Aided Design, 2003, 35(13): 1249-1259.

[5] Nam S H, Yang M Y. A Study on a Generalized Parametric Interpolator with Real-time Jerk-limited Acceleration[J]. Computer-Aided Design, 2004, 36(1): 27-36.

[6] Du Daoshan, Liu Yadong, Yan Cunliang,et al. An Accurate Adaptive Parametirc Curve Interpolator for NURBS Curve Interpolation[J]. Int. Adv. Manuf. Technol.,2007,32:999-1008.

[7] 曹宇男,王田苗,陈友东, 等. 插补前S加减速在CNC前瞻中的应用[J].北京航空航天大学学报，2007,33(5):594-599.

[8] 施法中. 计算机辅助几何设计与非均匀有理B样条 [M]. 北京：高等教育出版社，2001.