隧道坍方风险评价的未确知测度模型及工程应用

何美丽，刘霁,，刘浪，周健

（1.湖南城市学院 土木工程学院，湖南 益阳，413000；2.中南大学 资源与安全工程学院，湖南 长沙，410083）

塌方是大跨度公路隧道施工过程中常见的工程地质灾害之一。近年来，隧道工程发展极其迅速，国内大部分在建或已建的隧道均发生过不同程度的塌方。隧道塌方不仅给隧道施工带来巨大的困难，而且严重威胁着工程设备和人员安全，给工程带来巨大的经济损失和恶劣的社会影响。随着隧道工程建设的不断开展，对隧道塌方风险的定量化要求越来越高[1−2]，为此，国内外相继制订了一系列法律法规，如国际隧道协会颁布的Guidelines for Tunneling Risk Management[3]，2007年11月我国铁道部颁布了《铁路隧道风险评估与管理暂行规定》[4]，但在理论、方法体系的论述不多，也缺少实施层面的指导和工程实践范例。开展隧道塌方机制、评价和防治方法研究具有重大现实意义。近年来，人们对塌方的机制、预测、处治等方面进行了许多研究[1−2,4−14]。尤其在塌方预测方面，许多先进的计算理论与方法逐步引入到隧道塌方风险势评价中，如：张立新等[4]建立了隧道塌方失稳的尖点突变模型，并给出塌方与否的判据；周建昆等[5]编制了岩石公路隧道塌方分析事故树；周峰[6]提出了钻爆法施工的山岭隧道塌方风险模糊层次评估模型；袁龙[7]建立了隧道洞口段塌方风险模糊层次综合评估模型；Shin等[8−10]利用人工神经网络理论，提出一种隧道塌方灾害指标及评估系统，用于评估掌子面的塌方灾害水平；Fraldi等[9−11]根据 Hoek–Brown 破坏准则，借助微分学相关理论，推导出围岩破坏的精确解，用于预测岩石隧道洞顶的稳定性，并得到隧道任意交叉段塌方机制的解析解以及用解析和数值模拟方法评价圆形岩石隧道塑性破坏区；Yang等[12−13]据极限分析中的上限定理和Hoek–Brown破坏准则，得到了考虑水压力的圆形隧道滑动面的数值解，并根据非线性Hoek–Brown破坏准则分析了浅埋隧道塌方机制；安永林等[1]借鉴可拓学，建立了隧道坍方风险的可拓综合评估流程；李风云[14]基于支持向量机相关理论并结合隧道塌方的特点，建立了隧道塌方的支持向量机预测模型。上述新的理论和方法有其自身的特点，同时也存在一定不足，如：模糊综合评判法对各指标确定隶属度及赋予不同权重时，会带有一定的主观性和随意性[6−8]；人工神经网络方法存在收敛速度慢、易陷入局部最优及隐含层确定具有主观性等弱点；支持向量机所确定的边界抗干扰能力差、对噪声数据敏感等[14]。因此，上述分类方法还不能很好地指导隧道工程实践。影响隧道塌方风险的因素具有复杂性、多样性和非线性的特点，很难提出准确通用的判别准则，如何建立一种多参数综合评价模型对隧道塌方风险进行正确预测及抗震减灾具有重要意义。隧道塌方风险等级评价问题实质上是一个不相容问题，是内因和外因综合作用的结果，具有模糊性、复杂性和不确定性，其影响因素目前没有统一标准，部分指标也难以确定，各因素对隧道塌方的影响程度是一种未确知关系。在隧道塌方风险评价中，未确知测度评价方法与其他评价方法相比，未确知测度满足“归一性条件”及“可加性原则”，因而评价结果是科学的。未确知测度方法注意了评价空间的“有序性”，给出了比较合理的置信度识别准则，使评价结果更清晰合理，并且采用信息熵确定各指标权重，最大限度地利用了源数据的有效信息，避免了评价过程中的单纯主观臆断和片面性。为此，本文作者在前人研究工作的基础上，借鉴未确知数学理论和思想[15−17]，将隧道塌方与其影响因素之间的关系看成一种未确知系统，将未确知理论运用到隧道塌方风险定级评价中，同时引入信息熵理论[16−18]确定各指标的权重，以便较好地消除人为因素带来的偏差，使评价结果更符合实际，从而为工程的设计与施工提供合理的决策依据。

1 未确知测度评估原理

设隧道塌方风险评价对象ξ有n个，则评价对象空间 ξ={ξ1，ξ2，…，ξn}。对于每个评价的对象 ξi（i=1，2，…，n）有m个单项评价指标空间，即 X={X1，X2，…，Xm}，则 ξi可表示为 m 维向量 ξi={ξi1，ξi2，…，ξim}。其中：xij表示隧道塌方风险其评价指标的测量值。

对每个子项 xij（i=1，2，…，n；j=1，2，…，m），假设有p个评价等级{V1，V2，…，Vp}（本文将隧道塌方风险分为 4个类别，则 p=4）。记评价空间为 D，则D={V1，V2，…，Vp}。设Vk（k=1，2，…，p）为第k级评价等级，且 k 级比 k+1 塌方风险等级“高”，记为Vk＞Vk+1。若满足 V1＞V2＞…＞Vk，则称{V1，V2，…，Vp}是评价空间D的一个有序分割类[15−17]。

1.1 单指标测度评价向量

若μijk=μ（xij∈Vk）表示测量值xij属于第k个评价等级的程度，且要求满足：

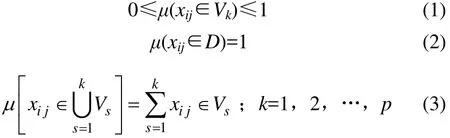
式（1）称为“非负有界性”，式（2）称为“归一性”，式（3）称为“可加性”。满足式（1）～（3）称为未确定测度，简称测度[16]。称矩阵为单指标测度评价矩阵，且有：

该矩阵的第 j个行向量（μj1，μj2，…，μjp）为 xij的单指标测度评价向量。

直线型未确知测度函数图见图1。在区间[ai，ai+1]上对应的未确知测度函数的表达式分别为：

图1 直线型未确知测度函数Fig.1 Straight-line UM function

在上述各函数表达式中，μi（x）在点ai左半区间上的值取 0，在区间[ai+1，ai+2]上与 μi+1（x）在（ ai,ai+1]上的图像相同；μi+1（x）在[ai−1，ai]上的图像与 μi（x）在[ai，ai+1]上的图像相同，μi+1（x）在ai+1左半区间上取值为0。

1.2 基于Shannon熵理论确定各指标权重

确定评价指标的权重时，多采用Delphi法和AHP法等主观赋权法，这会使评价结果可能由于人主观因素而形成偏差。信息论中，熵反映了信息无序化程度，其值越小，表明系统无序度越小，故可用信息熵评价所获系统信息的有序度及其效用，从数据本身所反映的信息的无序化效应值来计算权重系数，即由评价指标值构成的判断矩阵来确定其权重。它可尽量消除各指标权重计算的人为干扰，使评价结果更符合实际[17]。设 wj表示测量指标 Xj与其他指标相比具有的相对重要度，需满足：0≤wj≤1，且称wj为Xj重，w={w1，w2，…，wm}为指标权重向量，根据熵确定权重，即

显然，0≤vj≤1。令

因矩阵（4）已知，故可由式（6）～（7）求得wj。

1.3 多指标综合测度评价向量

令 μik=μ（R∈Vk）为评价样本属于 ξi第 k个评价类Vk的程度，则有：

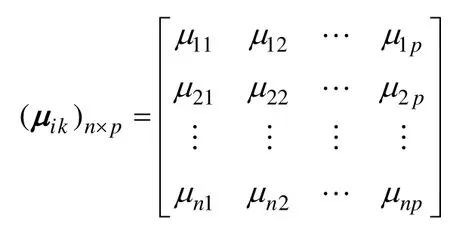
为多目标综合未确知测度评价矩阵，{μi1，μi2，…，μip}为ξi的多指标综合测度评价向量[15]。

1.4 属性识别模型

当{V1，V2，…，Vp}有序时，最大隶属度识别准则不再适用，为此，采用置信度准则[16−19]。设λ为置信度，取值范围通常为0.5＜λ＜1.0（常取0.6或0.7）[19]，且满足V1＞V2＞…＞Vp时，其识别模型为：

取 k直到满足式（9），则认为 xi属于 Vki类或 Vki级别。

2 隧道塌方风险评价的未确知测度模型

2.1 隧道塌方风险评价因子的确定

隧道坍方的发生、发展是一个复杂的过程，其影响因素很多，随机性大，且各因素之间呈高度的非线性。导致塌方的原因有很多，但总的说来，主要有自然因素、地质因素、勘察设计因素和施工因素共4种客观与主观因素[1,6−7,14]。建立隧道塌方风险的未确知测度评估模型时，还需考虑分析资料的易获性和代表性，经综合考虑选取围岩级别X1、开挖跨度X2、埋深X3、偏压角度 X4、地下水状况 X5、施工水平 X6这 6个特征参数指标作为未确知测度模型评估指标，其分级判据指标如表1所示[1,6−7]，评价流程见图2。表1中：地下水、施工技术和管理水平为定性因素；分级是用定性语言描述的，在计算法按表1量化值计算。在确定评价等级分类方案时，根据部分学者研究成果[2,6−7,14]、隧道坍方的特征和《铁路隧道风险评估与管理暂行规定》[3]，将坍方风险分为低度坍方风险（V1）、中度坍方风险（V2）、高度坍方风险（V3）和极高坍方风险（V4），如表1所示。

表1 隧道塌方评价指标及分级标准Table 1 Evaluation and grading standards for tunnel collapse

图2 隧道塌方风险的未确知测度评价流程Fig.2 Principle flow chart for proposed UM-based approach to assess risk of tunnel collapse

运用未确知测度理论对隧道塌方风险进行评价的基本步骤如下：

（1）确定隧道塌方风险的影响因素和分级标准。

（2）根据分级标准建立隧道塌方风险评价指标的单指标未确知测度函数。

（3）根据评价指标未确知测度函数和评价对象参数值建立评价矩阵。

（4）根据式（6）～（7），运用信息熵理论确定评价指标的权重。

（5）根据式（4）计算多指标综合测度评价向量。

（6）根据式（9），利用置信度识别准则对隧道塌方风险进行评价。

2.2 隧道塌方风险评价的未确知测度模型的建立及评价

为了验证本文提出的基于熵权未确知测度理论的隧道塌方风险评价方法的有效性和实用性，以武广（武汉—广州）客运专线浏阳河隧道 DⅡK1565+120～DⅡK1565+250 段为例[1]。该地段出现风化槽谷，其原始指标数据为：围岩Ⅴ级，开挖跨度约为 14 m，埋深 45 m，无明显偏压，地下水较发育，地质结构很复杂，施工技术和管理水平很高，开挖方法为三台阶法施工，其结果如表 2 所示。

表2 浏阳河隧道塌方评价指标及分级标准Table 2 Liuyang River tunnel collapse collapse risk factor and its evaluation results

根据单指标测度函数的定义和表1构建单指标测度函数以便求得各评价指标的测度。其各自的单指标测度函数分别见图3。由表1中各因子的取值，根据以上单指标测度函数（见图3），可求得该地段评价对象的单指标测度评价矩阵为：

图3 隧道坍方的评价指标体系Fig.3 Evaluation index system of tunnel collapse

利用信息熵理论确定各指标权重，据式（6）～（7）可得评价指标的权重向量w={0.173 4,0.132 8,0.173 4,0.173 4,0.173 4,0.173 4}。根据单指标矩阵和式（4）可求得样本1的多指标综合测度评价向量：{0.173 4，0，0.466 4，0.360 2}。

2.3 属性识别评价结果分析

取置信度λ=0.6，由多指标综合属性测度评价向量式（7）和置信度评价准则公式（8）得测度为 0.639 8＞0.600 0，则可以判别其风险等级为V3，即表示浏阳河隧道在该段的坍方风险属于“高度风险”级别。测试计算结果与实际结果及物元可拓分析法[1]的评价结果进行对比，结果如表3 所示。

从表3 可以看出：该隧道塌方风险评价样本未确知测度评价结果与实际情况基本吻合。从而说明本文隧道塌方风险评价模型的有效性和可行性。所以，将未确知测度分析模型应用于隧道塌方风险等级评价的判定中完全可行、高效可靠的，具有较高的实用价值。在隧道塌方风险评价中，未确知测度评价方法与其他评价方法相比，未确知测度满足“归一性条件”及“可加性原则”，因而，评价结果是科学的。此外，未确知测度方法注意了评价空间的“有序性”，给出了比较合理的置信度识别准则，使评价结果更加清晰、合理。并且采用信息熵确定各指标权重，最大限度地利用了源数据的有效信息，避免了评价过程中的单纯主观臆断和片面性。单指标测度函数图见图4。

表3 ZK122+575～ZK122+645段隧道塌方风险因素参数及其评价结果Table 3 ZK122+575～ZK122+645 section tunnel collapse risk factor parameters and its evaluation results

图4 单指标测度函数图Fig.4 UM function of evaluation indices

3 工程应用

3.1 案例1：青山岗隧道

青山岗隧道[7]是长沙—重庆高速公路中的 1座分离式双向4车道隧道，左洞起止桩号为ZK121+420～ZK122+665，全长 1 245 m；右洞起止桩号为YK121+388～YK122+615，全长1 227 m。采用新奥法原理设计、施工，衬砌为复合式衬砌。出口段为震旦系上统地层出露。左洞出口段ZK122+575～ZK122+645为浅埋地段且严重偏压，山体自然坡度为 35°～45°，覆盖层最薄处仅4 m，该段围岩为硅质岩，弱～微风化，岩层薄层状，岩石坚硬，节理裂隙发育，岩体呈块碎石镶嵌结构，地质勘察为IV～V级围岩，其稳定性差，比较容易发生塌方，且围岩为微透水层，渗水严重，局部滴状漏水，为此，有必要对此段进行塌方风险评估。根据已建立的塌方风险未确知测度评估模型对ZK122+575～ZK122+645段进行风险评估，其指标取值见表 4[7]。根据地质勘察资料，ZK122+575～ZK122+610段（记作 A）为 IV 级围岩，ZK122+610～ZK122+645段（记作B）为V级围岩，因此，把此段按围岩级别分为A和B2段进行塌方风险评估。

将评价结果与有关文献提供的隧道塌方风险情况及评判结果进行对比分析。利用本文方法预测的隧道塌方风险等级结果与实际结果及模糊综合评价法[6]所得评价结果进行对比，结果如表3 所示。周峰[6]根据最大隶属度原则得出ZK122+575～ZK122+610段隧道塌方发生概率的等级为Ⅲ级，即为偶尔发生。根据现场施工情况，青山岗隧道左洞自 2005-09-03从出口ZK122+645开始掘进，2005-11-23掘进到ZK122+575断面，据施工记录显示[7]，此段施工过程中经常出现小规模的塌方掉块，并且波及地表，引起地表开裂，沉降过大，由此可以说明本文构造的隧道塌方风险评估模型有一定的准确性和实际意义。结果表明：这 2种方法所得结果一致，进一步表明未确知测度模型在隧道塌方风险分级预测中的有效性与可行性。

3.2 案例2：马鞍山隧道

马鞍山隧道[8]位于诸（暨）永（嘉）（诸暨—永嘉）高速金华段，属分离式隧道。该隧道位于浙中中低山丘陵区，中间高，东西两端低，山顶海拔高程为370.9 m，地形自然坡度 35°～40°，地表植被发育。马鞍山隧道右洞为单向行车双车道隧道，长为181 m。隧道右线洞口段为浅埋偏压段，埋深为5～16 m，偏压角度大约为25°，3倍洞径内主要为全、强风化层，风化裂隙极发育，岩石破碎，呈角碎石状，结构松散，稳定性差，围岩级别为V级。由于马鞍山隧道右线洞口段为浅埋偏压地形，围岩稳定性差，隧道洞口容易发生塌方事故，因此，对隧道洞口段（K97+573～K97+593）进行塌方风险评估。根据已建立的洞口段塌方风险未确知综合评估模型，对马鞍山隧道洞口段塌方风险进行评估。

经计算得其多指标综合属性测度评价向量。在现场施工过程中，马鞍山隧道右洞洞口在进洞过程中发生塌方，地表由于隧道塌方产生了范围大约为12.5×3 m2的塌陷坑，最深达2.8 m。可以看出：模型计算结果和现场实际结果基本吻合，验证了评估模型的实用性和准确性。与实际情况、模糊综合评价法[7]的评价结果进行对比，结果如表4 所示。

表4 马鞍山隧道右洞洞口塌方评价指标及其评价结果Table 4 Evaluation and grading standards for tunnel collapse and its evaluation results

4 结论

（1）针对隧道塌方风险评价与其影响因素间高度的非线性复杂关系，引入未确知数学和信息熵理论，通过深入地挖掘隧道塌方的各种因素，选取围岩级别、开挖跨度、埋深、偏压角度、地下水状况、施工水平这6个特征参数指标作为塌方诱因，建立基于熵权的隧道塌方风险评价未确知测度模型，以期进一步提高我国隧道塌方风险评估与管理技术水平，为塌方的有效预防和防治提供依据。

（2）在评价过程中，将信息熵理论和未确知理论耦合到一个评价模型中，利用熵权来确定权重的方法，使得权重的确定有了一定的理论依据，减少了评价中人为主观因素的影响和评价结果的主观性，可提高隧道塌方风险等级评价模型结果的可信度。同时，置信度识别准则的应用使得评价结果更加准确、可靠。利用未确知测度模型对武广（武汉—广州）客运专线浏阳河隧道、青山岗隧道和马鞍山隧道坍方风险评估与实际情况一致，且评价结果直观、准确可靠，具有信息利用率高的优点。

（3）本文所建立的隧道塌方风险等级评价的未确知测度模型，计算方法简单，评价结果与实际结果较吻合，为隧道塌方风险等级评价方法提供了一条新的途径。值得注意的是：隧道塌方风险等级评价结论的准确性与可信度取决于所采用的评价指标及构造未确知测度函数的方法，因而需深入了解隧道塌方机制，详细分析各影响因素对隧道塌方风险等级的影响，构造更加广泛适用的未确知测度函数，提高隧道塌方风险等级评估模型的可靠性。

[1]安永林,彭立敏,吴波,等.隧道坍方突发性事件风险可拓法综合评估[J].中南大学学报:自然科学版,2011,42（2）:514−520.AN Yong-lin,PENG Li-min,WU Bo,et al.Comprehensive extension assessment on tunnel collapse risk[J].Journal of Central South University：Science and Technology,2011,42（2）:514−520.

[2]Eskesen S D,Tengborg P,Kampmann J,et al.Guidelines for tunnelling risk management:International tunnelling association,working group No.2[J].Tunnelling and Underground Space Technology,2004,19（3）:217−237.

[3]铁建设[2007]200号,铁路隧道风险评估与管理暂行规定[S].Railway Cconstruction[2007]No.200,The professional standard of People’s Republic of China[S].

[4]张立新,李长洪.突变理论及其在隧道失稳中的应用[J].工业建筑,2007,37（增刊）:863−865.ZHANG Li-xin,LI Chang-hong.Theory of mutation and its application in tunnel destabilization[J].Industrial Construction,2007,37（Suppl）:863−865.

[5]周建昆,吴坚.岩石公路隧道塌方风险事故树分析[J].地下空间与工程学报,2008,4（6）:991−998.ZHOU Jian-kun,WU Jian.Fault tree analysis of the collapse risk in rock highway tunnel[J].Chinese Journal of Underground Space and Engineering,2008,4（6）:991−998.

[6]周峰.山岭隧道塌方风险模糊层次评估研究[D].长沙:中南大学土木工程学院,2008:29−69.ZHOU Feng.Research on fuzzy-hierarchy assessment on mountain tunnel collapse[D].Changsha:Central South University.School of Civil Engineering,2008:29−69.

[7]袁龙.基于模糊层次综合评估法的隧道洞口段塌方风险评估[D].西安:长安大学公路学院,2010:24−56.YUAN Long.Risk assessment in tunnel portal landslide based on fuzzy AHP comprehensive evaluation[D].Xi’an:Changan University.School of Highway,2010:24−56.

[8]Shin J H,Kwon Y C,Jung Y S,et al.Methodology for quantitative hazard assessment for tunnel collapses based on case histories in Korea[J].International Journal of Rock Mechanics and Mining Sciences,2009,46（6）:1072−1087.

[9]Fraldi M,Guarracino F.Limit analysis of collapse mechanisms in cavities and tunnels according to the Hoek−Brown failure criterion[J].International Journal of Rock Mechanics and Mining Sciences,2009,46（4）:665−673.

[10]Fraldi M,Guarracino F.Analytical solutions for collapse mechanisms in tunnels with arbitrary cross sections[J].International Journal of Solids and Structures,2010,47（2）:216−223.

[11]Fraldi M,Guarracino F.Evaluation of impending collapse in circular tunnels by analytical and numerical approaches[J].Tunnelling and Underground Space Technology,2011,26（4）:507−516.

[12]Yang X L,Huang F.Collapse mechanism of shallow tunnel based on nonlinear Hoek−Brown failure criterion[J].Tunnelling and Underground Space Technology,2011,26（6）:686−691.

[13]Huang F,Yang X L.Upper bound limit analysis of collapse shape for circular tunnel subjected to pore pressure based on the Hoek–Brown failure criterion[J].Tunnelling and Underground Space Technology,2011,26（5）:614−618.

[14]李风云.隧道塌方风险预测与控制研究[D].长沙:中南大学土木工程学院,2011:41−67.LI Feng-yun.Study on tunnel collapse risk prediction and control[D].Changsha:Central South University.School of Civil Engineering,2011:41−67.

[15]王光远.论未确知性信息及其数学处理[J].哈尔滨建筑工程学院学报,1990,23（4）:52−58.WANG Guang-yuan.Uncertainty information and its mathematical treatment[J].Journal of Harbin Architecture and Engineering Institute,1990,23（4）:52−58.

[16]史秀志,周健,董蕾,等.未确知测度模型在岩爆烈度分级预测中的应用[J].岩石力学与工程学报,2010,29（Supp1）:2720−2727.SHI Xiu-zhi,ZHOU Jian,DONG Lei,et al.Application of unascertained measurement model to prediction of classification of rockburst intensity[J].Chinese Journal of Rock Mechanics and Engineering,2010,29（Supp1）:2720−2727.

[17]ZHOU Jian,LI Xi-bing.Integrating unascertained measurement and information entropy theory to assess blastability of rock mass[J].Journal of Central South University,2012,19（7）:1953−1960.

[18]薛剑光,周健,史秀志,等.基于熵权属性识别模型的岩体可爆性分级评价[J].中南大学学报:自然科学版,2010,41（1）:251−256.XUE Jian-guang,ZHOU Jian,SHI Xiu-zhi,et al.Assessment of classification for rock mass blastability based on entropy coefficient of attribute recognition model[J].Journal of Central South University:Science and Technology,2010,41（1）:251−256.

[19]程乾生.属性识别理论模型及其应用[J].北京大学学报:自然科学版,1997,33（1）:12−20.CHENG Qian-sheng.Attribute recognition theoretical model with application[J].Acta Scientiarum Naturalium Universitatis Pekinensis,1997,33（1）:12−20.