空位缺陷对zigzag型石墨烯纳米带电子结构的影响

徐慧，张丹，陈灵娜

（1.中南大学 物理与电子学院，湖南 长沙，410083；2.中南大学 材料科学与工程学院，湖南 长沙，410083）

人们对石墨纳米带的理论研究最早可以追溯到20世纪90年代[1−3]。然而，因为当时受实验条件的制约，石墨纳米带并未引起广泛关注和研究。直到2004年，Novoselov等分离出二维石墨烯[4]，制备出仅包含几个原子层的超薄石墨片甚至单层石墨片，该材料是目前世界上最薄的物质[5−7]。近年来，石墨烯纳米带作为一种新型的准一维碳基纳米材料，由于其具有优异的物理化学性能，在纳米电子学器件上具有广阔的应用前景。石墨烯纳米带可以分为2种：锯齿型（zigzag）石墨烯纳米带和扶手椅型（armchair）石墨烯纳米带。大量研究表明，对于所有宽度的锯齿型（zigzag）石墨烯纳米带均呈现出金属性。在石墨烯纳米带的制备过程中，不可避免地存在各种各样的缺陷如拓扑缺陷[8−9]、空位缺陷[10−15]、吸附原子[16−19]等。在理论方面，欧阳方平等[20−22]研究了单、双空位缺陷及边缘缺陷等对石墨烯纳米带的电子结构和输运性质的影响；Zhang等[23]研究了具有边缘缺陷的zigzag石墨烯纳米带自旋极化效应。由此可见，缺陷的引入对石墨烯纳米带的电子结构有重要影响。但是，到目前为止，缺陷对纳米带电子结构的影响机理还有待进一步研究。为此，本文作者利用基于密度泛函理论的第一性原理研究空位缺陷对zigzag石墨烯纳米带的电子结构的影响。

1 计算模型与方法

Zigzag石墨烯纳米带的几何结构优化和电子结构的计算采用基于密度泛函理论（DFT）方法[24]的 VASP程序包完成。势文件采用广义梯度近似（GGA）和Perdew-Wang 91（PW91）交换关联函数势能。为了避免石墨烯纳米带之间的相互作用，故在Y方向的真空层厚度选取为10×10−10m，X方向的真空层厚度也选取为10×10−10m。在进行结构优化和计算中，一维的简约布里渊区积分通过Monkhost-Pack方法自动产生，K点取样为1×1×11的网格。结构弛豫收敛判据设为每个原子受力小于0.01 eV/nm。计算能带时，按照Line模式产生K点，K点取样是1×1×21的网格。

为了确保石墨烯纳米带的结构不会因为缺陷的存在而发生明显的变化，选取宽度为8的zigzag型石墨烯纳米带作为研究对象，其超胞构型包括5个单胞，完整的zigzag（8,5）石墨烯纳米带的单胞显示见图1（其中：E为石墨稀纳米带能，Ef为其费米能）。在超胞中去掉几个碳原子形成了空位缺陷，如图2所示。为了避免出现悬挂键，石墨烯纳米带的边缘以及缺陷的边缘都用氢原子饱和。图2所示为含缺陷zigzag（8,5）石墨烯纳米带超胞在弛豫之后的构型，其中图2（a）所为单空位缺陷的构型，图2（b）所示为双空位缺陷构型，图2（c）所示为三空位缺陷构型，图2（d）所示为四空位缺陷构型。

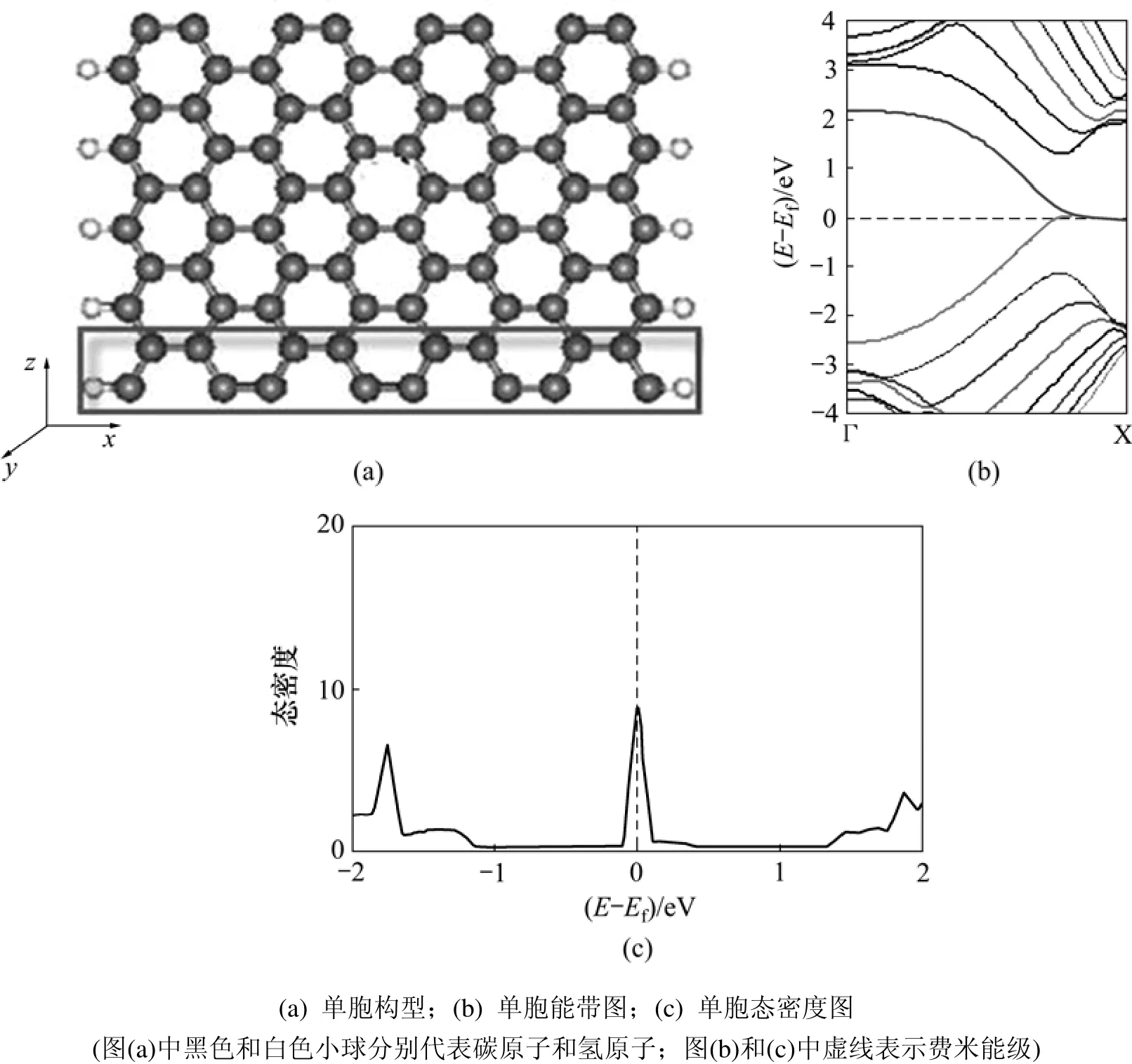
图1 zigzag（8,5）石墨烯纳米带的单胞构型、能带和态密度图Fig.1 Unit cell structure,bands and density of states of zigzag（8,5）graphene nanoribbons

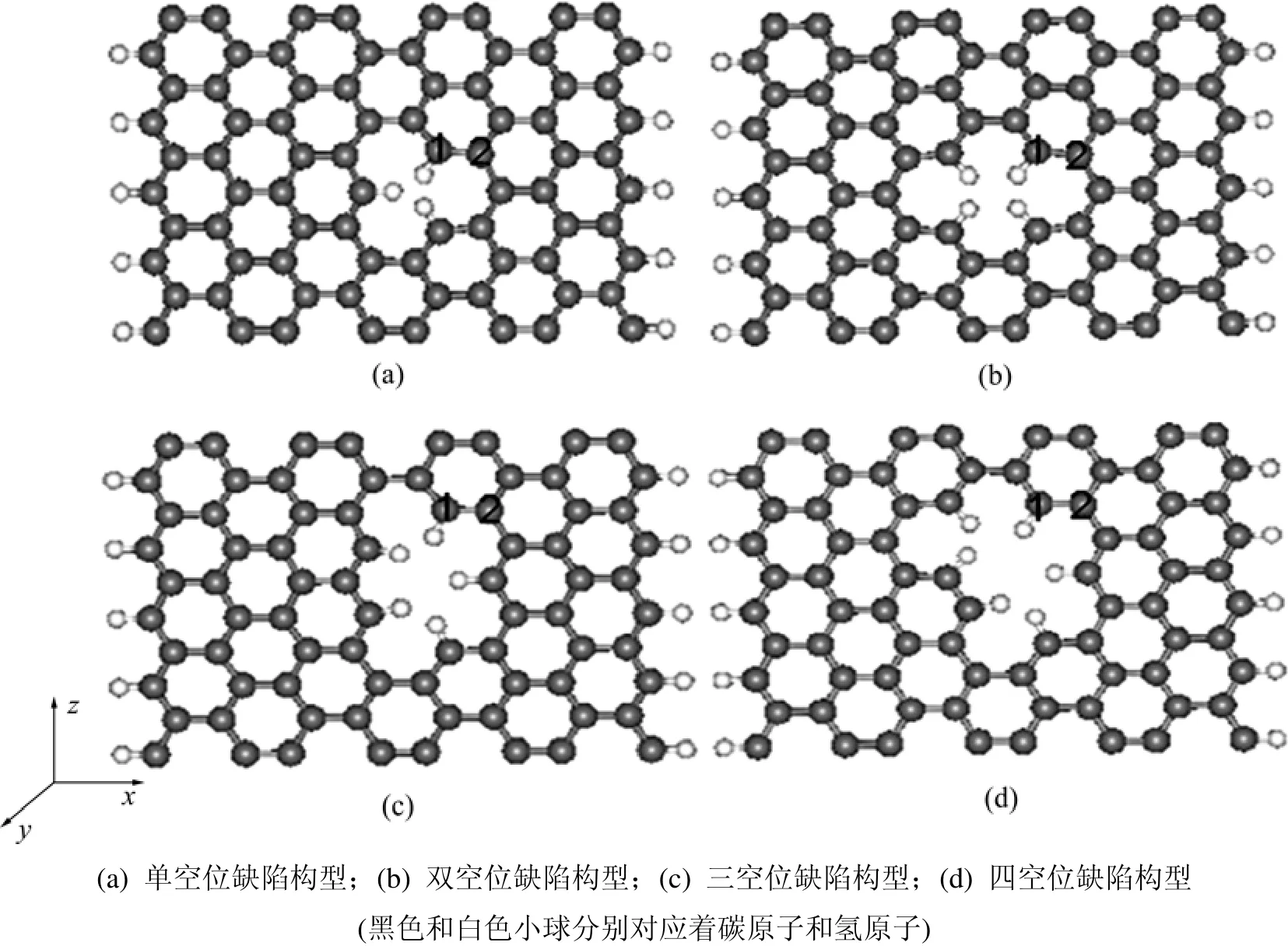
图2 结构弛豫之后的含缺陷zigzag（8,5）石墨烯纳米带构型Fig.2 Structures of defected zigzag（8,5）graphene nanoribbons after relaxed

2 计算结果与讨论

图3所示为含不同空位缺陷的zigzag（8,5）石墨烯纳米带的能带结构，对应的超胞构型如图2所示。在图3中，虚线代表费米能级的位置。每种构型的能带右边的能带图是对其相应的左边的费米能级附近能带图的放大图。从图 1（b）可见：完整的 zigzag（8,5）石墨烯纳米带在费米能级处有2条能带简并，表现出零带隙的准金属性质，这与欧阳方平等[21]的研究结果相一致。图3（a1）和（a2）所示为单空位缺陷的石墨烯纳米带的能带结构，可以发现费米能级处出现了3条局域能级，这些局域能级与费米能级相交，并且费米能级附近的 π和π*能带之间的距离增加，这与文献[20]所报道的对单空位zigzag石墨烯纳米带的特征相同，验证了本文计算方法的可靠性。在单空位缺陷构型的基础上再去掉1个碳原子形成双空位缺陷，能带结构发生了显著改变，在费米能级附近出现了2条局域能带，并且费米能级附近的π和π*能带之间的距离几乎没有增加，如图3（b1）和（b2）所示。当空位缺陷的数目增加到3个时，能带结构图同单空位缺陷构型的相类似，在费米能级附近同样有3条局域能级。然而，当空位缺陷的数目变为偶数4个时，能带结构图与双空位缺陷构型的类似，在费米能级附近有2条局域能级。由此可以得出：当空位的碳原子数为偶数时，费米能级处存在2条能带，并且费米能级附近的π和π*能带之间的距离几乎没有增加；相反，当空位缺陷的碳原子数为奇数时，费米能级处出现3条能带，并且费米能级附近的π和π*能带之间的距离明显增大。这4个缺陷构型的能带图中都有能带与费米能级相交，即含缺陷的zigzag石墨烯纳米带仍然显示出类金属性的电子结构特征。这是因为空位缺陷的引入只是改变了缺陷局部的结构，并没有改变zigzag石墨烯纳米带锯齿边缘的结构[20]。

结合图2的模拟构型，通过计算可以得出：缺陷碳原子位置的对称性对zigzag石墨烯纳米带的电子结构有显著影响。从图1（b）可以看出：完整的zigzag石墨烯纳米带由于对称性高，故导带底和价带顶在费米能级处发生高度简并。从图3可见：含缺陷的zigzag石墨烯纳米带由于缺陷的引入，对称性被破坏，从而引起费米面处的能级发生分裂，简并度降低。在二空位缺陷和四空位缺陷构型中，由于缺陷处具有镜面对称性，因此，虽然能带也发生了分裂，费米面多出 2条能级，但是没有完全消除简并；在单空位和三空位缺陷构型中，对称性完全被破坏，简并完全消除，费米面多出3条能级。

图3 含缺陷zigzag（8,5）石墨烯纳米带的能带图Fig.3 Bands of defected zigzag（8,5）graphene nanoribbons

图4 含缺陷zigzag（8,5）石墨烯纳米带的态密度图和分波态密度图Fig.4 Density of states and projected density of states of defected zigzag（8,5）graphene nanoribbons

为了进一步理解空位缺陷对ziazag型石墨烯纳米带电子结构的影响，给出4种含缺陷zigzag（8,5）石墨烯纳米带的态密度图（DOS）和分波态密度图（PDOS），如图4所示。从图4可见：在态密度图中，虚线代表费米能级；位点1和2均代表缺陷边缘的碳原子，在缺陷超胞构型图中用红色数字标识，如图2所示。从图4（a1）和（a2）可以看出：单空位缺陷构型的态密度在费米能级处出现了1个尖锐的峰，该峰主要是位点1的碳原子所致。这是因为位点1碳原子产生的PDOS峰远远大于位点2碳原子产生的PDOS峰；对于双空位缺陷，费米能级处的DOS峰比较平坦，该峰同样是位点 1的碳原子所致，如图 4（b1）和（b2）所示。从图4（c1），（c2），（d1）和（d2）可以观察到费米能级附近出现2个DOS峰，而且位点1的碳原子产生的PDOS峰明显明显高于位点2碳原子产生的PDOS峰。这表明含有三空位缺陷和四空位缺陷的石墨烯纳米带附近的能带主要是位点1碳原子所致。由此可以得出：费米能级附近的能带部分是由缺陷态引起的[25]，且缺陷边缘处紧靠缺失的碳原子对缺陷能级的贡献最大，缺陷周围的氢原子几乎对缺陷能级没影响。

完整的zigzag石墨烯纳米带的碳原子成键时其电子被束缚在原子核周围，自由导电的电子较少，电子的局域性较强。当中间缺失1个碳原子时，用氢原子饱和相当于用氢原子掺杂，但是，由于氢原子间的相对位置较近，并且氢原子对电子的束缚能力较弱，故增加了碳原子之间的相互作用，最终导致缺陷处的自由电子增多，在费米能级附近出现的概率增大；当空位缺陷处的碳原子数多于2个时，由于空位间的距离较大，不利于电子的相互转移；此外，碳原子的饱和度降低，电子的浓度减小，致使费米能级附近的峰值越来越低。

3 结论

（1）含空位缺陷的zigzag石墨烯纳米带都呈现出类金属性的电子结构特征，其电子结构与缺失碳原子的数量及缺陷位置附近碳原子的饱和度密切相关。

（2）缺陷的存在会破坏体系能级的简并，引入缺陷能级。当缺失的碳原子数目为偶数时，费米能级附近的简并态只是部分消除，只产生2条能级；当缺失的碳原子数目为奇数时，费米能级附近的简并态消除，产生3条能级。随着空位缺陷的增加，缺陷处碳原子的不饱和度也增加，并且电子的浓度减小，从而费米能附近的态密度峰发生相应衰减。

[1]Fujita M,Wakabayashi K,Nakda K,et al.Peculiar localized state at zigzag graphite edge[J].Phys Soc Jpn,1996,65:1920−1923.

[2]Nakada K,Fujita M,Dresselhaus G,et al.Edge state in graphene ribbons:nanometer size effect and edge shape dependence[J].Phys Rev B,1996,54:1195−1196.

[3]Miyamoto Y,Nakada K,Fujita M.First-principles study of edge states of H-terminated graphitic ribbons[J].Phys Rev B,1999,59:9858−9861.

[4]Novoselov K S,Geim A K,Morozov S V,et al.Electric field effect in atomically thin carbon films[J].Science,2004,306:666−669.

[5]Wang J J,Zhu M Y,Outlaw R A,et al.Free-standing subnanometer graphite sheets[J].Appl Phys Lett,2004,85:1265−1267.

[6]Novoselov K S,Jiang D,Sched in F,et al.Two-dimensional atomic crystals[J].Proceeding of the National Academy of Sciences of the United States of America,2005,102（30）:10451−10453.

[7]Zhang Y,Tan Y W,Stormer H L,et al.Experimental observation of the quantum Hall effect and Berrys phase in grapheme[J].Nature,2005,438:201−204.

[8]Stone A J,Wales D.Theoretical studies of icosahedral C60and some related species[J].Chem Phys Lett,1986,128:501−503.

[9]Xu S C,Irle S,Musaev D G,et al.Quantum chemical study of the dissociative adsorption of OH and H2O on Pristine and defective graphite surfaces:Reaction mechanisms andkinetics[J].Phys Chem C,2007,111:1355−1365.

[10]Telling R H,Ewels C P,El-Barbary A A,et al.Wigner defects bridge the graphite gap[J].Nature Mater,2003,2:333−337.

[11]El-Barbary A A,Telling R H,Ewels C P,et al.Structure and energetics of the vacancy in graphite[J].Phys Rev B,2003,68:144107.

[12]Krasheninnikov A V,Nordlund K,Lehtinen P O,et al.Adsorption and migration of carbon adatoms on carbon nanotubes:Density-functional ab initio and tight-binding studies[J].Phys Rev B,2004,69:073402.

[13]Krasheninnikov A V,Nordlund K,Sirviö M,et al.Formation of ion-irradiation-induced atomic-scale defects on walls of carbon nanotubes[J].Phys Rev B,2001,63:245405.

[14]Amorim Rodrigo G,Fazzio A,Antonelli Alex,et al.Divacancies in graphene and carbon Nanotubes[J].Nano Lett,2007,7:2459−2462.

[15]Lee G D,Wang C Z,Yoon E,et al.Diffusion,coalescence and reconstruction of vacancy defects in graphene layers[J].Phys Rev Lett,2005,95:205501.

[16]Lehtinen P O,Foster A S,Ayuela A,et al.Magnetic properties and diffusion of adatoms on a graphene sheet[J].Phys Rev Lett,2003,91:017202.

[17]Nordlund K,Keinonen J,Mattila T.Formation of ion irradiationinduced small-scale defects on graphite surfaces[J].Phys Rev Lett,1996,77:699−702.

[18]Talapatra S,Ganesan P G,Kim T,et al.Irradiation-induced magnetism in carbon nanostructures[J].Phys Rev Lett,2005,95:097201.

[19]Ma Y,Foster A S,Krasheninnikov A V,et al.Nitrogenstimulated magnetism in graphite and carbon nanotubes[J].Phys Rev B,2005,72:205416.

[20]欧阳方平，王焕友，徐慧,等.单空位缺陷对石墨纳米带电子结构和输运性质的影响[J].物理学报,2008,57（11）:71332−71338.OUYANG Fang-ping,WANG Huan-you,XU Hui,et al.Study on electronic structure and transport properties of grapheme nanoribbons with single vacancy defects[J].Acta Phys Sin,2008,57（11）:71332−71338.

[21]欧阳方平，徐慧，李明君,等.Armchair 型石墨纳米带的电子结构和输运性质[J].物理化学学报，2008,24（2）:328−332.OUYANG Fang-ping,XU Hui,LI Ming-jun,et al.Electronic structure and transport properties of armchair graphene nanoribbons[J].Acta Phys Chim Sin,2008,24（2）:328−332.

[22]欧阳方平,徐慧,魏辰.Zigzag型石墨纳米带电子结构和输运性质的第一性原理研究[J].物理学报,2008,57（2）:1073−1077.OUYANG Fang-ping,XU Hui,WEI Chen.First-principles study of electronic structure and transport properties of zigzag graphene nanoribbons[J].Acta Phys Sin,2008,57（2）:1073−1077.

[23]Zhang Y T,Jiang H,Sun Q F,et al.Spin polarization and giant magnetorestance effect induced by magnetization in zigzag grapheme nanoribbons[J].Phys Rev B,2010,81:165404.

[24]李燕峰,徐慧,马松山,等.单壁碳管直径对电子结构的影响[J].中南大学学报:自然科学版,2005,36（1）:44−48.LI Yan-feng,XU Hui,MA Song-shan,et al.Effect of diameter on electronic structure of open-ended single wall carbon nanotubes[J].Journal of Central South University:Science and Technology,2005,36（1）:44−48.

[25]欧阳方平,徐慧,林峰.双空位缺陷石墨纳米带的电子结构和输运性质研究[J].物理学报,2009,58（6）:4132−4136.OUYANG Fang-ping,XU Hui,LIN Feng.The electronic structure and transport properties of graphene nanoribbons with divacancies defects[J].Acta Phys Sin,2009,58（6）:4132−4136.