面齿轮啮合过程中压力角对齿面摩擦生热的影响分析
2012-11-29何国旗严宏志胡威何瑛舒陶量
何国旗 ,严宏志,胡威,何瑛,舒陶量
(1.中南大学 机电工程学院,高性能复杂制造国家重点实验室,湖南 长沙,410083;2.湖南工业大学 机械工程学院,湖南 株洲,412000;3.湖南理工职业技术学院 资源工程系,湖南 湘潭,411104)
面齿轮传动是一种圆柱齿轮与圆锥齿轮相啮合的齿轮传动,其面齿轮属于特殊的圆锥齿轮,是用尺寸与其啮合的渐开线圆柱齿轮尺寸相同或者相近的刀具经范成而得到的[1]。面齿轮传动由于具有结构简单、传动重合度大、动力分流效果好、振动小等诸多优点[1],面齿轮的动力分流传动装置在武装直升机传动系统中得到应用。由于武装直升机在飞行过程中的载荷及转速较高,传动系统摩擦生热较大,而且啮合过程中齿面各点的载荷及相对速度不同,使得轮齿上温度场分布不均匀,引起齿轮热弹性变形,不仅会消除齿轮传动间隙,还将引起齿廓形状发生改变,这将极大地影响面齿轮的传动性能、润滑性能和可靠性,导致传动失效,因此,齿面温度成为影响面齿轮传动质量的重要技术指标。Litvin等[1]对面齿轮传动的啮合进行了研究,从啮合几何学原理上分析了根切和顶尖的条件,同时发展了点接触面齿轮。邓小洈[2]在试验的基础上建立了摩擦副导热的数学模型及边界条件,采用数值计算方法对摩擦副温度场在不同工况下的温度场进行计算,得到了摩擦副的温度分布状况;龙慧等[3]系统分析了圆柱齿轮啮合过程中主、从动轮轮齿的绝对滑动速度和相对滑动速度,建立了齿面摩擦因数和摩擦热流量的计算方法,并分析了其沿啮合面的分布规律以及相关的影响因素。肖望强等[4]介绍了非对称齿轮摩擦热流量的计算方法,并分析了其沿啮合面的分布规律以及相关的影响因素,推导了轮齿本体温度的热平衡方程,建立了轮齿有限元温度分析的模型。李政民卿等[5]对面齿轮的啮合理论进行了研究,主要集中于面齿轮的齿面生成、面齿轮齿宽的限制条件、无安装误差及有安装误差的齿接触分析、运动误差、重合度齿面曲率和齿面速度等。目前,人们对面齿轮啮合过程中齿面摩擦生热的研究特别是压力角对齿面摩擦生热的影响研究较少。圆柱齿轮和面齿轮接触表面的摩擦热流量由齿面的相对滑动速度、接触压力和齿面摩擦因数共同决定[2]。为此,本文作者通过对面齿轮齿面几何特征进行分析,在全膜润滑的假设条件下,从齿面的相对滑动速度、接触压力和齿面摩擦因数等几个方面研究面齿轮啮合过程中齿面摩擦生热以及受压力角的影响,以便为面齿轮的设计提供有效的理论依据。
1 面齿轮啮合时齿面相对滑动速度及影响因素分析
1.1 面齿轮啮合时齿面相对滑动速度形成分析
在面齿轮啮合过程中,由于圆柱齿轮和面齿轮的尺寸和转速不同,将导致两轮齿在啮合点沿切线方向的速度不相等,使得两轮齿齿面产生相对滑动[2−3]。
如图1所示,设圆柱齿轮的齿面IΣ和面齿轮的齿面ΣII某个时刻在N点啮合,在各自所在的坐标系中,其矢量r1和r2表达式分别为:
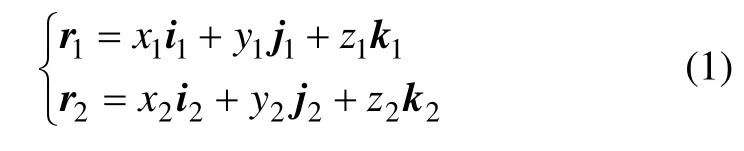
在时间dt内,圆柱齿轮的齿面ΣI移动到ΣI′,面齿轮的齿面ΣII移动到ΣII′′,点N运动到N′,该点在齿面ΣI上移到N1,在齿面ΣII上移到N2。
点N随各自坐标系的运动速度描述为:

图1 面齿轮传动时齿面接触点的运动描述Fig.1 Meshing point movement description of face-gear drive
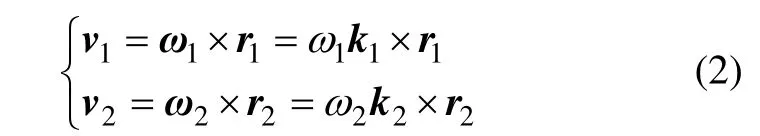
点N随同各自坐标系的相对速度为:


1.2 压力角对齿面相对滑动速度影响分析
本文算例中面齿轮传动的参数如下:面齿轮传动的模数为5,面齿轮的齿数为40,圆柱齿轮的齿数为17。圆柱齿轮及面齿轮的材料均为45号钢,圆柱齿轮进行表面淬火处理,硬度(HRC)为 40~45,面齿轮进行调质处理,硬度(HB)为220~240。齿轮啮合采用L-AN32全损耗系统用油喷油润滑,润滑油的初始温度和空气温度为 25 ℃,弹性模量E为 2.16×1011N·m2,泊松比ν为0.25;面齿轮系统扭矩T为20 kN·m,输入转速n1为2 000 r/min。
当压力角分别为20°和25°时,两齿轮接触面切向绝对滑动速度和相对滑动速度沿啮合区间的分布如图2所示。图2中v1和v2分别表示圆柱齿轮和面齿轮沿接触切线方向绝对滑动速度,vs为啮合点沿接触切线方向相对滑动速度;v1(20°)和v1(25°)表示压力角分别为20°和25°时圆柱齿轮沿接触切线方向绝对滑动速度;v2(20°)和v2(25°)表示压力角分别为 20°和 25°时面齿轮沿接触切线方向绝对滑动速度;vs(20°)和vs(25°)表示压力角分别为 20°和 25°时为啮合点沿接触切线方向圆柱齿轮和面齿轮的相对滑动速度。
从图2可知:压力角的改变对绝对滑动速度和相对滑动速度有较大的影响,压力角为 25°与压力角为20°相比,圆柱齿轮和面齿轮在啮合过程中绝对滑动速度增大,而圆柱齿轮和面齿轮的相对滑动速度随着压力角的增大而减小。

图2 不同压力角的面齿轮齿面沿接触切线方向绝对滑动与相对滑动速度分布Fig.2 Absolute and relative sliding velocity distribution at tangent direction of different pressure angels
2 面齿轮啮合区中的接触应力的确定
2.1 面齿轮啮合区中接触应力的计算
根据赫兹理论对接触物体表面几何关系的分析可知:物体表面之间有相同距离的点在公切面上将形成类似于椭圆的区域[6−7]。设面齿轮传动中,和分别为啮合点处圆柱齿轮齿面的两主曲率;和分别为啮合点处面齿轮齿面的两主曲率。正交主平面与公切面交线的交点分别为(x1,y1)和(x2,y2)。对于点接触的面齿轮传动,啮合点处形成接触椭圆,根据接触点主曲率和两弹性体弹性系数与接触椭圆区域的关系可知,接触区域椭圆长短半轴ρx和ρy分别为:

式中:iμ和Ei(i=l,2)分别为圆柱齿轮和面齿轮材料的泊松比和弹性模量;系数u和v为椭圆积分函数。
按照赫兹接触理论,在接触椭圆表面上,接触应力按椭圆体分布,其最大接触应力σmax在接触椭圆中心[8]。因此,面齿轮传动啮合点处的最大接触应力σmax为:

式中:ρx为椭圆的长半轴半径;ρy为椭圆的短半轴半径。当x=0,y=0时,椭圆中心发生最大应力为:

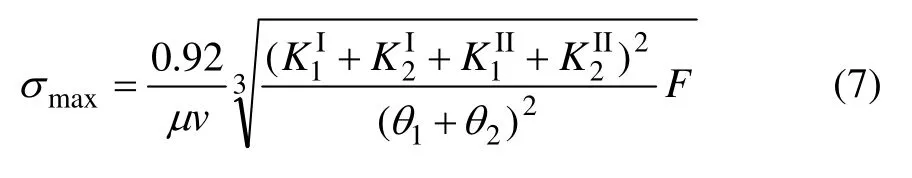
2.2 压力角对面齿轮啮合区中接触应力的影响分析
对面齿轮啮合区中的接触应力进行仿真分析,分析结果如图3所示。横坐标从左至右分别为双齿啮合区下界点即双齿齿根啮入点,单齿啮合区下界点即单齿啮入点,啮合节点,单齿啮合区上界点即单齿啮出点,双齿啮合区上界点即双齿齿顶啮出点。
图3 中σH(20°)和H(25°)分别表示面齿轮压力角为 20°和 25°时啮合区中的接触应力。由图3可以看出不同压力角的面齿轮从齿根啮入到齿顶啮出齿面接触应力沿啮合线的分布和变化规律。当压力角为 20°时,在单对齿啮合区下界点面齿轮的齿面接触应力达到一个啮合周期中的最大值,达到850 MPa。当压力角为25°时,无论单齿啮合区还是双齿啮合区,下界点面齿轮的齿面接触应力都呈明显下降趋势,齿面最大接触应力σHmax为 780 MPa,且啮合点接触区平均压力σc也减小。

图3 不同压力角的面齿轮齿面接触应力σH变化曲线Fig.3 Contact stress curves of face-gear at different pressure angels
3 面齿轮啮合时齿面摩擦生热流量的确定
3.1 面齿轮齿面接触域的摩擦因数
根据Barone等[9−10]提出的摩擦因数计算公式,对于面齿轮齿面的任意啮合点C,摩擦因数cμ可表示为:

式中:wcτ为单位宽度上的载荷;η0为润滑油黏度;v12为啮合点处相对滑动速度;vr为啮合点处卷汲速度。
在面齿轮啮合过程中,接触点处的相对滑动速度以及卷汲速度随啮合点位置的变化而变化,因此,齿面摩擦因数在啮合过程中也是变化的[8]。齿面接触区的摩擦因数不仅与面齿轮轮齿啮合位置有关,而且与面齿轮齿面粗糙度、转速、接触载荷等因素有关;同时,还受润滑油黏度和齿轮本体温度的影响。其中,转速及润滑油黏度是影响齿轮摩擦因数的主要因素。
3.2 面齿轮啮合区滑动摩擦热计算
面齿轮啮合齿面间的摩擦热主要包括:齿面间的滑动摩擦、滚动摩擦以及金属弹塑性变形引起的摩擦3个方面。在面齿轮啮合过程中,轮齿接触表面的摩擦热流量与接触压力、齿面的相对滑动速度和齿面摩擦因数等有关。齿面上由摩擦产生的热能一部分通过热传导进入齿轮齿体,而另一部分则由作用啮合齿面的润滑油通过强制对流传热而冷却扩散。因此,啮合齿面产生的摩擦热流量对高速齿轮温度的改变和分布以及热的平衡有重要影响[8]。面齿轮啮合区滑动摩擦热可按下式计算:

3.3 压力角对面齿轮啮合区滑动摩擦热的影响
对面齿轮啮合区滑动摩擦热进行仿真分析,得到面齿轮的摩擦热流量沿啮合线的分布如图4所示。图4 中qc(20°)和qc(25°)分别表示压力角为 20°和 25°条件下沿啮合线的摩擦热分布。
由图4可知:压力角为25°与20°相比,双齿啮合区面齿轮齿面摩擦热流量明显要小,压力角为20°时,双齿啮合区面齿轮下界点面齿轮齿面摩擦热流量为120 kN/m2;而压力角为25°时,双齿啮合区面齿轮下界点面齿轮齿面摩擦热流量约为75 kN/m2。在单齿啮合区,压力角为25°与20°相比,虽然单齿啮合区面齿轮齿面摩擦热流量要大,但相差很小。
因此,面齿轮轮齿在啮合区各点处的摩擦热流量随着工作齿侧压力角的增大而减小,在齿根处摩擦热流量最大值减小的幅度最大。

图4 不同压力角的面齿轮摩擦热流量qc沿啮合线的分布Fig.4 Face-gear friction heat flux distribution along meshing line at different pressure angels
4 齿面间摩擦热流量的分配
4.1 齿面间摩擦热流量的分配计算
由于材料、导热系数以及边界热阻等不同,接触面上产生的摩擦热流量向两齿轮的热量也不相同。由于面齿轮啮合状况非常复杂,摩擦因数μ通过实测或经验数据来确定,一般推荐μ=0.045~0.065[10],本文取μ=0.050。设两啮合轮齿之间摩擦热分配因子为λ,则齿轮任意啮合点C处的摩擦热流量qc分作2部分qc1与qc2,分别流入圆柱齿轮和面齿轮,则2个齿轮各自输入的热量分别为[6−8]:

摩擦热分配因子λ的表达式为:

式中:β1和β2为 2个齿轮材料的导热系数;ρ1和ρ2为2个齿轮材料的密度;c1和c2为2个齿轮材料的比热容;vτ1和vτ2为2个齿轮啮合点C处的切向速度。
4.2 压力角对齿面间摩擦热流量分配的影响
从齿根啮入到齿顶啮出,圆柱齿轮热分配系数λ1沿啮合线增大,面齿轮热分配系数λ2沿啮合线减小。对面齿轮啮合齿面间摩擦热流量分配进行仿真分析,热分配系数λ1和λ2沿啮合线的分布如图5所示,热分配系数λ1和λ2与轮齿参与啮合顺序及压力角有关,使齿轮在啮合线方向热分配系数变化率减小。图5中λ1(20°)和λ1(25°)为压力角分别为 20°和 25°时圆柱齿轮热分配系数;λ2(20°)和λ2(25°)为压力角分别为 20°和 25°时面齿轮热分配系数。
从齿根啮入瞬时到啮合节点,对于圆柱齿轮来讲,压力角为 20°的热分配系数比压力角为 25°的热分配系数要小,但从啮合节点到齿顶啮出瞬时,压力角为20°的热分配系数比压力角为25°的热分配系数要大。面齿轮则与圆柱齿轮相反。而且,从齿根啮入瞬时到啮合节点,圆柱齿轮的热分配系数均小于面齿轮。从啮合节点到齿顶啮出瞬时,圆柱齿轮的热分配系数均大于面齿轮的热分配系数。但是,圆柱齿轮和面齿轮在压力角为 25°时的热分配系数变化比压力角为 20°时的要小。

图5 不同压力角面齿轮热分配系数λ沿啮合线的分布Fig.5 Face-gear heat partition coefficient distribution along meshing line at different pressure angels
5 结论
(1)在面齿轮啮合过程中,压力角的改变对啮合齿面的绝对速度和相对滑动速度有很大的影响,随着压力角的增大,绝对滑动速度增大,而相对滑动速度则随着压力角的增大而减小。
(2)压力角增大,则圆柱齿轮、面齿轮沿啮合线的热分配系数变化率减小。
(3)面齿轮轮齿在啮合区各点处的摩擦热流量随着压力角的增大而减小,在齿根处摩擦热流量最大值减小的幅度最大。因此,适当增加压力角,有利于减少齿面摩擦生热。
[1]Litvin F L,Wang J C,Bossler R B,et al.Application of face-gear drives in helicopter transmissions[R].Scottsdale:NASA Technical Memorandum 105655,1991: 1−10.
[2]邓小洈.添加剂作用下滑动摩擦副温度场及胶合性能的研究[D].重庆: 重庆大学动力工程学院,2004: 25−46.DENG Xiao-wei.Study on temperature and scuffing properties for the sliding friction pair on considering oil additives[D].Chongqing: Chongqing University.College of Power Engineering,2004: 25−46.
[3]龙慧,张广辉,罗文军.旋转轮齿瞬时接触应力和温度的模拟分析[J].机械工程学报,2004,40(8): 24−29.LONG Hui,ZHANG Guang-hui,LUO Wen-jun.Modeling and analysis of transient contact stress and temperature of involutes gears[J].Chinese Journal of Mechanical Engineering,2004,40(8): 24-29.
[4]肖望强,李威,韩建友.非对称齿廓渐开线齿轮传动的热分析[J].农业机械学报,2006,37(12): 164−167.XIAO Wang-qiang,LI Wei,HAN Jian-you.Thermal analysis of involute gear transmission with unsymmetric tooth profile[J].Transaction of the Chinese Society for Agricultural Machinery,2006,37(12): 164−167.
[5]李政民卿,朱如鹏.面齿轮传动的承载接触分析[J].南京航空航天大学学报,2010,42(2): 219−223.LI Zheng-min-qing,ZHU Ru-peng.Load tooth contact analysis on face gear driver[J].Journal of Nanjing University of Aeronautics & Astronautics,2010,42(2): 219−223.
[6]Taburdagitan M,Akkok E.Determination of surface temperature rise with the rmoelastic analysis of spur gears[J].Wear,2006,261: 656−665.
[7]Long H,Lord A A,Gethin D T,et al.Operating temperatures of oil lubricated medium speed gears: Numerical models and experimental results[J].Journal of Aerospace Engineering,2003,217(2): 80−103.
[8]邱良恒,辛一行,王统,等.齿轮本体温度场和热变形修形计算[J].上海交通大学学报,1995,29(2): 79−86.QIU Liang-heng,XIN Yi-xing,WANG Tong,et al.A calculation of bulk temperature and thermal deflection of gear tooth about profile modification[J].Shanghai: Journal of Shanghai Jiaotong University,1995,29(2): 79−86.
[9]Barone S,Borgianni L,Forte P.Evaluation of the effect of misalignment and profile modification in face gear drive by a finite element meshing simulation[J].Transactions of ASME,Journal of Mechanical Design,2004,126: 916−924.
[10]Guing M,de Vaujany J P,Jacquin C Y.Quasi-static analysis of a face gear under torque[J].Compute.Methods Appl Mech Engrg,2005,194: 4301−4318.
