平面曲线切割函数的一阶和二阶导数
2012-11-28苑柳宁岳崇山
苑柳宁,岳崇山
(河北北方学院理学院,河北 张家口075000)
Peter J.Gibin和Donal B.O'shea在参考文献 [1]中讨论了平面闭曲线的双切圆的存在性问题。在上述作者的论文中,切割函数是一个重要的概念和工具。参考文献 [2-6]从各种角度研究了切割函数的一些基本的性质,特别是参考文献 [6]讨论了平面曲线的切割函数对参数s的连续性和可导性,从理论上证明了切割函数是光滑的,即它存在任意阶导数。本文的工作是通过具体地计算切割函数的一阶和二阶导数在不连续点的极限情况,希望得到的结果是:它们的不连续点都是可去间断点,进而得到切割函数的一阶和二阶导数的显式的表达式。这个工作的意义在于:倘若切割函数的一阶和二阶导数具有显式的表达式,那么我们就可以试图寻找平面曲线的凹凸性与其切割函数的凹凸性之间的关系。
1 基本概念
约定(s)为平面上的具有任意阶导数的曲线,称之为光滑曲线,这里参数s为弧长。
定义1.1 设(s)= {(s),y(s)}为平面曲线,(s)=(s)为曲线的单位切向量,(s)= {-y′(s),x′(s)}为曲线的单位法向量,κ(s)=x′(s)y″(s)-s″(s)y′(s)为曲线的相对曲率,称
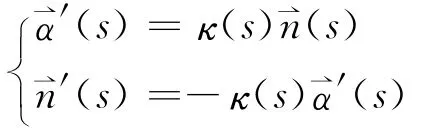
为平面曲线的Frenet公式。
定义1.2 设(s)为平面曲线,k(s)为其相对曲率,(s0)是曲线上一点。称
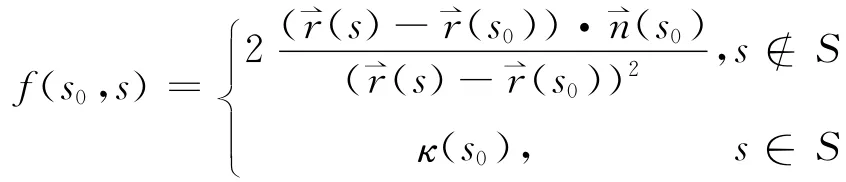
为曲线(s)的切割函数。这里S= {s|(s)=(s0)}。参考文献 [6]的定理2.1表明切割函数是连续的。
2 主要结果
设平面曲线(s)在点s,s0处的向径,单位切向量和单位法向量分别为(s)(s)(s)和(s0),,记
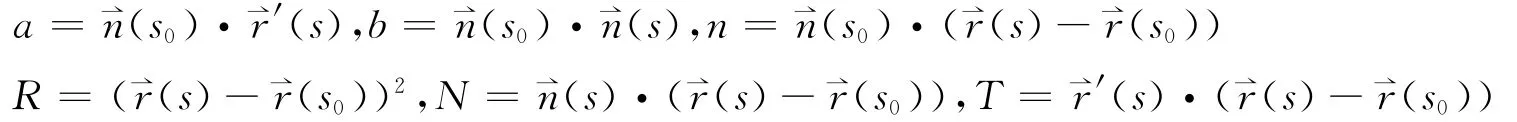
那么a,b,n,R,N,T都是关于参数s的光滑实函数。下面来研究它们的性质。
引理2.1a,b,n和R,N,T与它们各自的导数之间满足公式
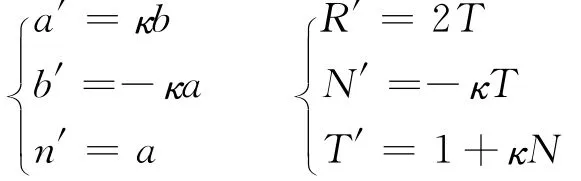
这里κ表示曲线在s处的曲率。
证明 由切割函数的表达式可知,
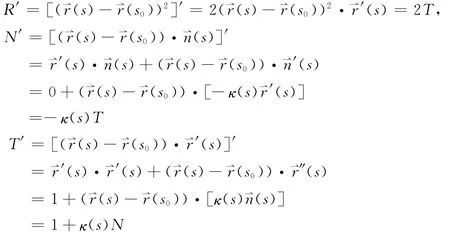
同理可证a′=κb,b′=-κa,n′=a。
根据函数a,b,n,R,N,T的定义容易得到下面的结果。
引理2.2 当时,
(1)P1= {a,b,n,R,N,T}中的元素除了b趋于1外,其余元素都趋于0。
(2)P2={xy|x,y∈P1}中元素除了b2趋于1外,其余元素都趋于0。
(3)P3={xyz|x,y,z∈P1}中元素除了b3趋于1外,其余元素都趋于0。
定理2.1 适当地补充值之后,切割函数的一阶导数处处连续。
证明 使用定理2.1的两组公式可知:当s∉S时,切割函数的一阶导数存在,其表达式为
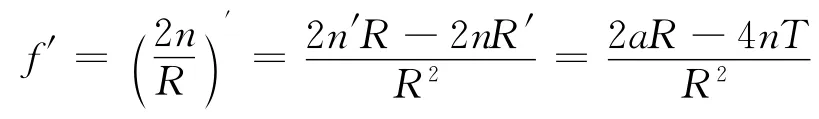
此时切割函数的一阶导数连续。下面我们来考察s∈S时,f′的可导性。为此,设g=2aR-4nT,h=R2。由引理2.1可以计算下面的结果。
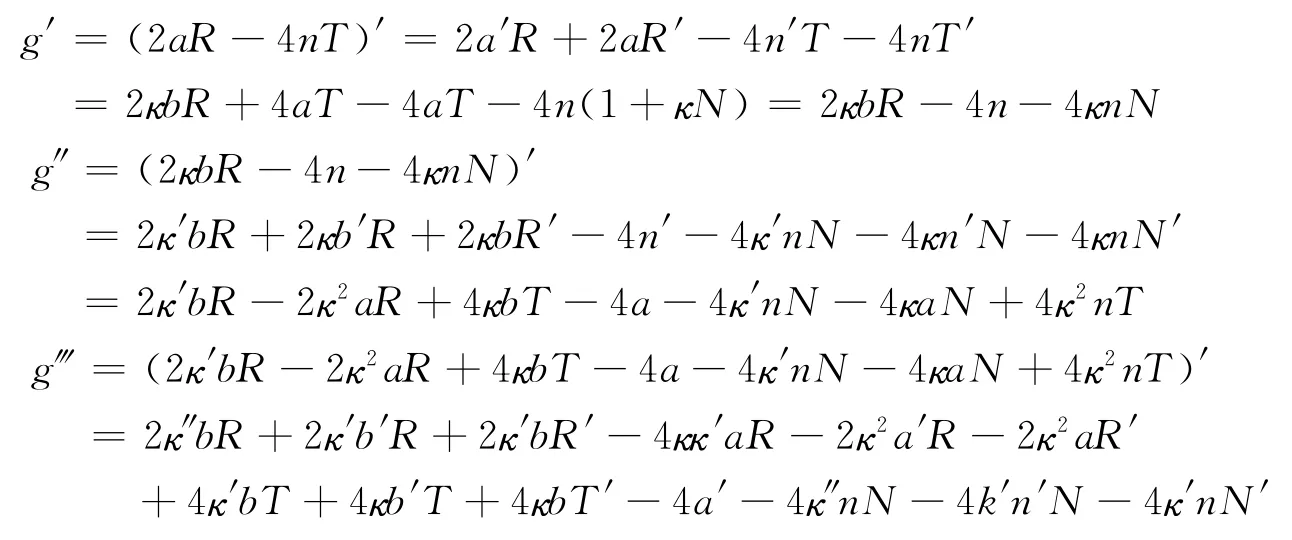
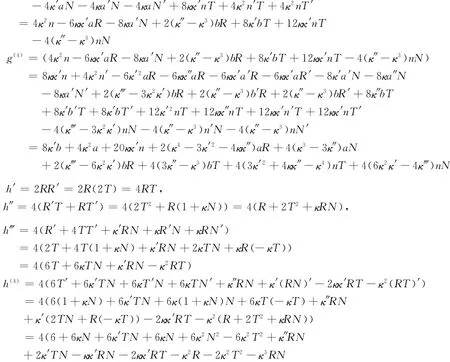
=4(6κ2N2-8κ2T2+(κ″-κ3)RN-3κκ′RT+8κ′TN-κ2R+12κN+6)由引理2.2可知当(s)→(s0)时,
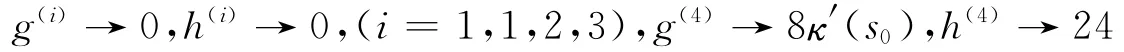
所以

这样在间断点补充值κ′(s0)/3之后,切割函数的一阶导数处处连续。事实上,可以将切割函数的一阶导数扩充为:
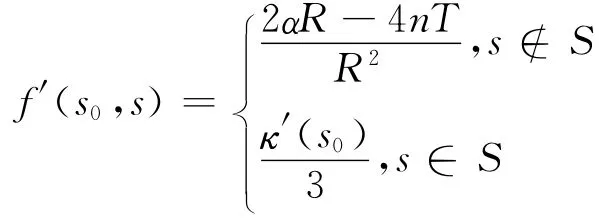
下面来考察切割函数的二阶导数的存在性和连续性。
引理2.3 设G=R3,则当s→s0时,G(i)→0,(i=1,1,2,3,4,5),G(6)→720
证明
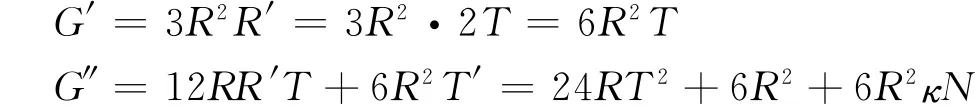
下面的计算中,反复使用引理2.1的公式,复合函数求导法则以及求导的四则运算.受篇幅所限,只列出了计算结果,而省略了大部分的计算步骤。
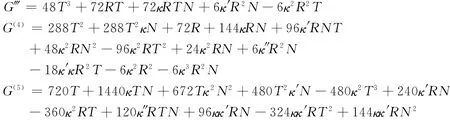
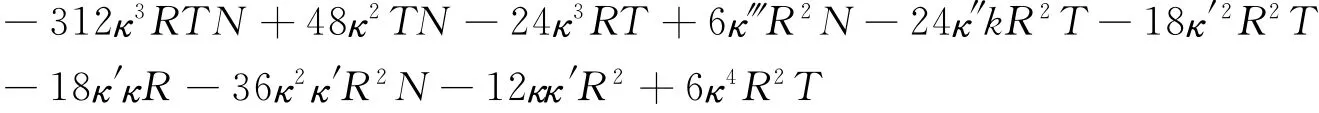
由引理2.2可知,当(s)→(s0)时,G(i)→0,(i=1,2,3,4,5),观察G(5)的表达式可知G(5)中求导取极限之后能够得到非零常数的项只有720T,而720T的求导取极限等于720,所以当(s)→(s0)时,G(6)→720。
引理2.4 设
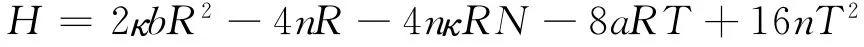
则当s→s0时,H(i)→0,(i=1,2,3,4,5),H(6)→120κ″(s0)。
证明
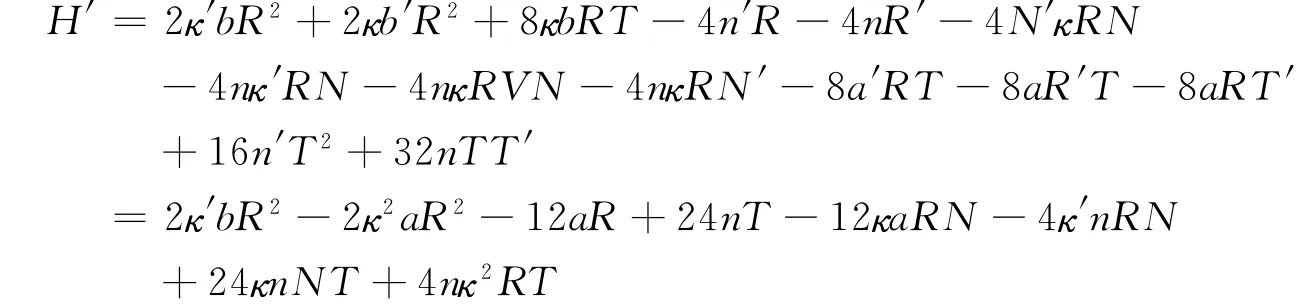
与引理2.3类似的原因,下面的计算也只列出了计算结果:

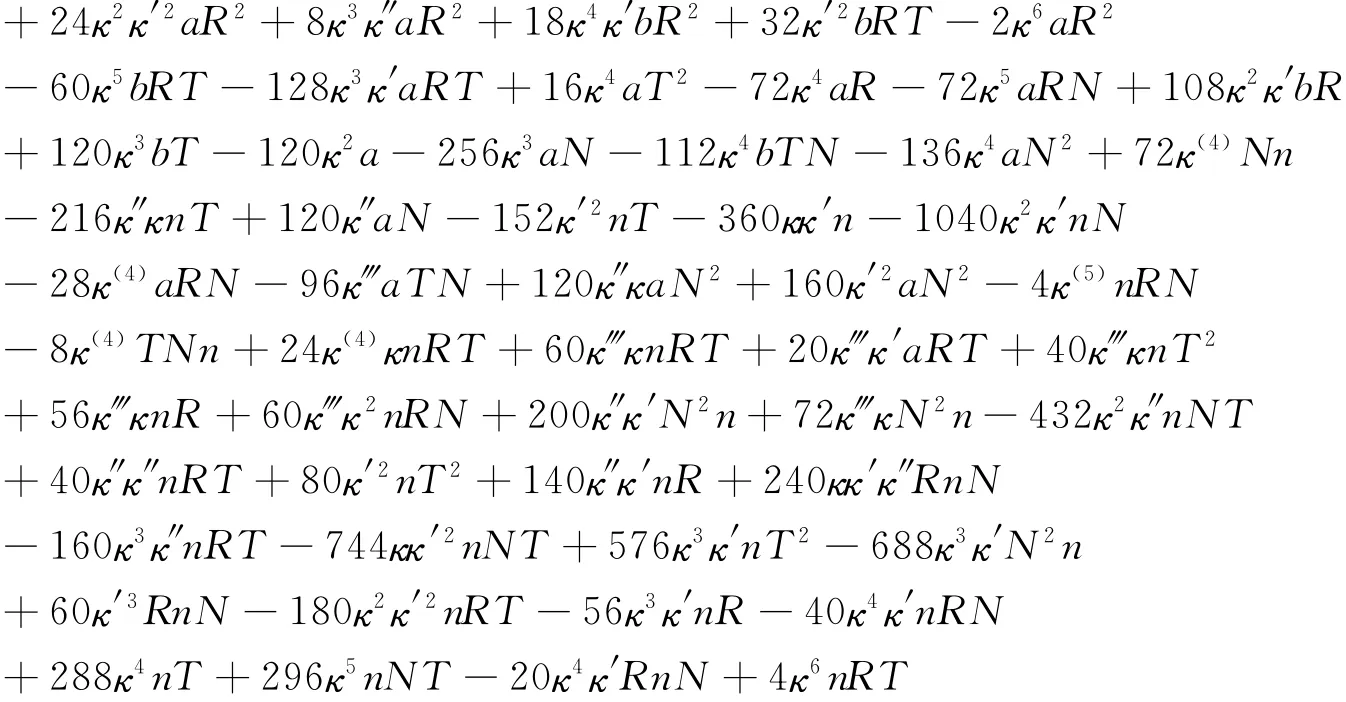
由引理2.2可知,当(s)→(s0)时,H(i)→0(i=0,1,2,3,4,5)。观察H(5)的表达式可知H(5)中求导取极限之后能够得到非零常数的项只有120κ″bT,而120κ″bT求导取极限等于120κ″(S0),所以当(s)→(s0)时,H(6)→120κ″(s0)。
定理2.2 适当地补充值之后,切割函数的二阶导数处处连续。
证明 使用定理2.1的两组公式及定理2.2得到的切割函数的一阶导数的表达式可知:当s∉S时,切割函数的二阶导数存在,其表达式为
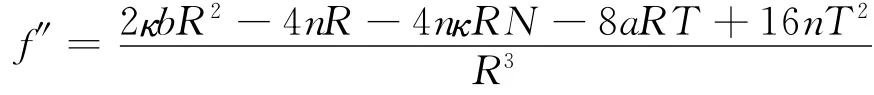
此时切割函数的二阶导数连续。下面来考察s∈S时,f″的可导性。为此,设H=2κbR2-4nR-4nκRN-8aRT+16nT2,G=R3。由引理2.3和引理2.4可知
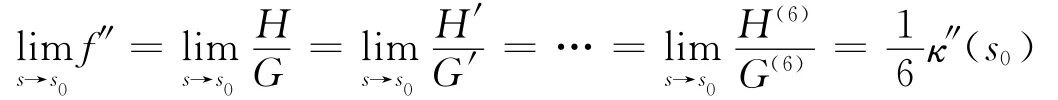
这样在间断点补充值κ″(s0)/6之后,切割函数的二阶导数处处连续。事实上,可以将切割函数的一阶导数扩充为:
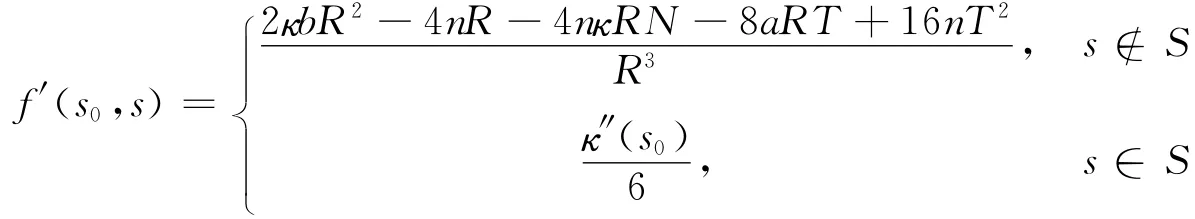
定理2.1和定理2.2的证明给出了平面曲线的切割函数的一阶和二阶导数的处处连续的具体的表达式,这有助于找到平面曲线的凹凸性与其切割函数的凹凸性之间的关系。
[1]Gibin PJ,O’shea DB.The bitangent sphere problem [J].Am Math Month,1990,97:5-23.
[2]岳崇山,宋旭华.切割函数为常值的曲线的一个结果 [J].河北北方学院学报:自然科学版,2010,26(03):13-15.
[3]岳崇山.切割函数的运动不变性 [J].河北北方学院学报:自然科学版,2010,26(05):10-13.
[4]岳崇山,张蒲修.切割函数与参数选择的关系 [J].河北北方学院学报:自然科学版,2011,27(05):10-12.
[5]岳崇山.切割函数关于第二参数的分析性质 [J].河北北方学院学报:自然科学版,2012,28(02):15-16.
[6]岳崇山,宋旭华,景海斌.平面曲线的切割函数的分析性质 [J].河北北方学院学报:自然科学版,2010,26(04):14-16.
