弹性阻尼耦合轮对动力学特性分析

王军平，黄运华，陈 倩，金 鑫

（西南交通大学 机械工程学院，四川成都610031）

在传统轮对、独立旋转车轮和耦合轮对3种轮轨导向系统中，传统轮对具有曲线上自导向和直线上自对中的优点：当轮对中心偏离轨道中心线时，在滚动圆半径差引起的左右车轮行驶距离差和蠕滑力的作用下可以自动返回轨道中心。然而，由于采用了具有一定斜度的锥形踏面，传统轮对不可避免地存在蛇行运动，限制了其运行速度的进一步提高，从而具有一定的局限性。但在所有轮轨导向系统中，传统轮对的应用最为广泛，技术也最为成熟。独立旋转车轮一般是将车轮通过轴承等装配到车轴的两端，左右车轮可以绕轴无相互影响地转动，其优点为消除了轮对的蛇行运动，临界速度得到了提高，但同时失去了曲线上的自导向和直线上的自对中能力。这种轮对可以通过采用较大等效斜度的踏面来增大横向重力刚度，依靠较大重力复原力来抑制轮对向单侧贴靠的趋势。独立旋转车轮一般轮缘磨耗严重，易发生脱轨事故，因此在世界范围内采用较少。耦合轮对是一种新型的轮轨导向系统，轮对的左右车轮是通过耦合器连接在一起的，既不完全独立也不完全固结。通过调节耦合器的耦合度，可以得到不同的动力学性能。当耦合度选取适当值时，耦合轮对可以兼备传统轮对和独立旋转车轮的优点，一定程度上消除了二者的缺陷，同时具有较好的曲线自导向和直线自对中能力，抑制了轮对蛇行运动，提高了临界速度。耦合轮在汽车行业中应用广泛，但由于耦合器研制技术等的限制，还未能在铁道车辆行业中得到实际应用。耦合轮对耦合器的形式可以有弹性阻尼、离心、气动、电磁、液压等多种形式［1］，由于其性能的优越性，非常有必要对不同形式的耦合轮对进行深入分析。

本文着重研究不同耦合度（耦合刚度和阻尼）下弹性阻尼耦合轮对（Elasto Damper Coupled Wheelset）车辆的动力学性能，并讨论耦合度变化对车辆动力学性能的影响，文中的耦合轮对均指弹性阻尼耦合轮对，用EDCW表示，车辆系统指转向架前后轮对均装有EDCW的车辆系统。

1 动力学计算模型

1.1 单个EDCW模型

图1 EDCW模型

图1所示为单个EDCW基本力学模型，其中K和C分别为耦合刚度和阻尼系数，当左右车轮有不同的旋转角时，可以得到不同的耦合力矩。假设左右轮的旋转角分别为φwL和φwR，则相应的旋转角速度分别为和此时，耦合力矩为：

通过调节耦合度，可以使轮对得到不同的特性，当耦合度趋于无穷大时，该轮对可看作传统轮对，同时当耦合度趋于无穷小时，轮对可看作为独立旋转车轮。

1.2 EDCW车辆及线路模型

铁道车辆是一个多刚体、多自由度、非线性振动的复杂系统，各部件之间通过弹簧和减振器等相连接。在不考虑车辆之间的相互影响，即以单个车体为研究对象时，可得到EDCW车辆动力学计算模型如图2所示。各刚体自由度的选择如下：

车轮：横移ywi，点头φwLi和φwRi，摇头ψwi；

构架：横移yfk，点头φfk，摇头ψfk，侧滚θfk，浮沉zfk。

车体：横移yc，点头φc，摇头ψc，侧滚θc，浮沉zc。其中k=1、2，分别代表前、后转向架；i=1～4分别代表1～4位轮对。因为EDCW左右车轮的点头角速度不一定相同，所以分别用φwLi和φwRi表示。整个车辆的自由度为31个。

图2 EDCW车辆动力学计算模型

本文分析所采用的轨道为60kg／m钢轨，车轮踏面为LM磨耗型踏面，轮轨摩擦系数为0.4。曲线通过性分析中采用的激扰为超高和曲率，直线稳定性分析中采用的初始激扰为1位轮对7mm横向位移，均不考虑轨道不平顺。曲线线路是由一段超高和曲率都固定的圆曲线及其两端各有一段超高和曲率都不断变化的缓和曲线组成。具体线路设置为直线（30m）→缓和曲线（100m）→圆曲线（100m）→缓和曲线（100m）→直线，其中圆曲线半径为400m，外轨最大超高120mm。

2 运动方程

在图2所示车辆系统中，车轮、转向架构架、车体等均视为刚体且结构对称，即不考虑各部件自身的变形，同时假设前后转向架各项参数都一致，各刚体的坐标系的原点均在质心上。在坐标系中，x方向为纵向，指向车辆前进方向，y轴为横向，在轨道平面内垂直于x轴指向车辆前进方向右侧，z轴为垂向，垂直轨道理论平面向下。

EDCW车辆的构架和车体的受力情况与传统轮对相似，故不再赘述，这里仅将EDCW的运动方程罗列如下：

轮对横移：

轮对摇头：

轮对点头：

方程中，φwsi=（φwLi+φwRi）／2，φwdi=（φwLi-φwRi）／2，

式（2）～式（5）中，Mw为轮对质量，kg；r0为轮对标称滚动圆半径，m；φsewi为线路实际超高角，rad；v为车辆前进速度，km／h；Rwi为实际曲线半径，m；TLyi、TRyi为左右车轮横向蠕滑力，kN；TLxi、TRxi为左右车轮纵向蠕滑力，kN；TLzi、TRzi为左右车轮垂向蠕滑力，kN；NLyi、NRyi为左右车轮法向力的横向分力，kN；NLzi、NRzi为左右车轮法向力的垂向分力，kN；Fpwyi为一系悬挂横向力，kN；Iwy、Iwz分别为轮对绕y、z轴的惯性矩，kg·m2；φwi为轮对侧滚角，rad；a为左右轮轨接触点的横向间距之半，m；rLi、rRi为左右车轮的滚动圆半径，m；Mpwzi为一系悬挂摇头力矩，kN·m；MLyi、MRyi为左右车轮自旋蠕滑力矩在y轴的分量，kN·m；MLzi、MRzi为左右车轮自旋蠕滑力矩在z轴的分量，kN·m；Ci为耦合阻尼，kN·m·s／rad；Ki为耦合刚度，kN·m／rad。

3 动力学性能分析

3.1 不同耦合度下的直线稳定性分析

图3和图4所示分别为EDCW车辆系统临界速度随耦合刚度和阻尼的变化情况，其中耦合刚度和阻尼的单位分别为N·m／rad和N·m·s／rad，tra表示传统轮对。

研究发现，临界速度随耦合度的变化可以分为3个阶段。

图3 临界速度随耦合刚度的变化情况

图4 临界速度随耦合阻尼的变化情况

第1阶段：在小耦合度时，EDCW蛇行临界速度可以达到很高的值，并随着耦合度的增加呈递减趋势。例如，当耦合刚度和阻尼分别为10N·m／rad和100 N·m·s／rad时，临界速度为1 086km／h；当耦合刚度和阻尼分别取值为100N·m／rad和5 000 N·m·s／rad时，临界速度为355km／h。

第2阶段：耦合度取中间值（耦合刚度为103～105N·m／rad，阻尼为0～104N·m·s／rad）时，EDCW 车辆系统不稳定，并且其不稳定性有一定的特殊性。

第3阶段：较大耦合度时，车辆系统均稳定且临界速度逐渐增大并趋于稳定值。例如，取耦合刚度和阻尼分别为5×105N·m／rad和0时，临界速度为208km／h，临界速度随耦合刚度或阻尼的增加逐渐增加，当耦合刚度和阻尼取值分别达到108N·m／rad和5×104N·m·s／rad时临界速度达到314km／h，且不再随耦合度的增大而增大。当耦合刚度取值超过108N·m／rad或阻尼取值超过1×106N·m·s／rad时临界速度均为314km／h，并保持稳定。对相同参数，相同条件下的传统轮对车辆进行分析可知，其临界速度亦为314km／h，说明大耦合度下的耦合轮对与传统轮对性能相当，这与相关文献［1-2］所得的结论是吻合的。

同时对比图3和图4可以发现，耦合阻尼并不会引起EDCW系统的不稳定，而在小阻尼情况下，EDCW有较大的不稳定刚度区间，这种不稳定性随着耦合阻尼的增大而逐渐消失，说明耦合刚度的增大并不能改善系统的稳定性，而耦合阻尼对稳定性的影响效果较为显著。

图5为EDCW稳定性与同参数、同条件下的传统轮对稳定性对比，其中耦合刚度K=100N·m／rad、耦合阻尼C=1 000N·m·s／rad，纵坐标为1位轮对横向位移。由图5（b）可以看出，当速度达到315km／h时，传统轮对在初始激扰下不再收敛，而EDCW在该速度下收敛性依旧良好，说明EDCW的蛇行临界速度高于传统轮对；从图5（a）可以看出，在低于传统轮对的临界速度时，EDCW的收敛性同样优于传统轮对，蛇行失稳频率也小于传统轮对。

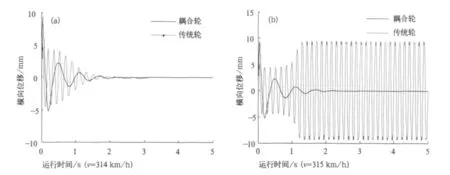
图5 传统轮对和EDCW的稳定性比较

图6 不同耦合度时的稳定性

图6所示为不同耦合度时的车辆稳定性曲线，由图6（a）可以看出，在稳定的小耦合度情况下，当速度较低时轮对无法回到轨道中心线，运行情况与独立旋转车轮相似，由于计算中所选用的轮轨摩擦系数比较大，所以车轮一直紧靠轮缘一侧，但运行状态稳定；在速度较高时对中性能良好，且随着速度的增加收敛速度加快。分析可知，虽然低速时轮对贴靠轮缘一侧运行，但运行稳定、随着速度的提高，轮对逐渐返回中心线，临界速度较高，因此小耦合度在高速列车中采用是一个比较理想的选择。

由图6（b）可以看出，在不稳定的中间耦合度情况下，车辆的不稳定性具有一定的特殊性，在较低速度时车辆蛇行运动不收敛，但其蛇行幅值较小，没有达到轮缘内侧与轨道的间隙值（9mm），说明此时的速度并未超出蛇行临界速度，但轮轨导向力不足使其无法收敛。随着速度的增加，车辆逐渐变得收敛，速度在200～448 km／h的范围内时车辆稳定，超出该范围时系统再次发散，但蛇行幅值达到了轮缘与轨道间的间隙值，说明高速下的不稳定是由于运行速度超出了蛇行临界速度而造成的。因此，中等耦合度（蛇行运动不稳定的耦合度区间）只适用于中等速度的运行状态，在高／低速时均无法满足要求，然而，车辆在运行中无法避免起／停以及较低速等状态，因此，该区间的耦合度不可采用。

图7 EDCW曲线通过性能比较

3.2 曲线通过性能

3.2.1 纵向蠕滑力导向机理

纵向蠕滑力能够产生一定的偏转力矩，在车辆通过曲线时起导向作用，传统轮对由于存在一定的踏面锥度，当轮对中心偏离轨道中心线（在曲线上为纯滚线）横移量为yw时，在纵向蠕滑力的作用下就产生一个偏转力矩，假设为Mz，其表达式为［3］：

式中f11为纵向蠕滑系数；λ为车轮踏面等效锥度；b为左右滚动圆距离之半。Mz在直线上起复位作用，在曲线上起导向作用。由于独立旋转车轮不产生纵向蠕滑力，因而无法实现直线上自对中和曲线上的自导向作用。而对于耦合轮对而言，其性能可以通过耦合刚度和阻尼来进行调节，在使轮轨间产生一定的蠕滑力来导向的同时提高车辆运行速度等其他性能。纵向蠕滑力的导向机理是本文研究EDCW曲线通过性能重要依据之一。

3.2.2 曲线通过性能分析

曲线通过性能是机车车辆动力学研究的重要内容之一，良好的曲线通过性能将大大减小轮轨间的磨耗及作用力，从而降低运营成本；反之，车辆曲线通过性能差，导向力不足，轮轨间将产生巨大的横向力，造成轮轨的严重磨耗，甚至发生脱轨事故［4］。因此，很有必要对EDCW车辆系统曲线通过性能进行研究。

本文以EDCW车辆以86km／h的恒定速度通过第1.2节所述曲线模型时的仿真结果作为参考分析其曲线通过性能。

对EDCW曲线通过性能进行分析可知，随着耦合度的增加，EDCW的曲线通过性能逐渐向传统轮对靠拢，但无法将其超越，其原因为EDCW纵向蠕滑力产生的偏转力矩始终无法超越左右车轮固结在一起的传统轮对。

图7所示为当刚度K=100N·m／rad时，在不同的耦合阻尼下EDCW曲线通过性能与传统轮对的对比图。图7（a）～（d）中，曲线下半部分为车辆前进方向1位轮对外侧轮轨接触点参数，上半部分为2位轮对外侧轮轨接触点参数。由7（a）图可以看出，小耦合度时，轮对横移量在过渡曲线时已经达到最大值，随着耦合度的提升，轮对在过渡曲线上向最大横移量的过渡越来越平缓；由图7（b）～（d）可以看出，耦合轮对转向架前轮对轮对冲角、轮轨横向力、脱轨系数均大于传统轮对，而后轮对对应各值均小于传统轮对；从图7（e）可以看出，耦合轮对的最大轮缘磨耗明显大于传统轮对。由于耦合轮对各参考量极限值和转向架前后轮对差值均大于传统轮对，因此，其曲线通过性能也劣于传统轮对。

值得注意的是如图7（f）所示，虽然耦合轮对的轮缘磨耗大于传统轮对，但其踏面磨耗却小于传统轮对，耦合轮对踏面磨耗值随耦合度的增加呈抛物线状，先下降再升高，但其值恒小于传统轮对。究其原因为耦合轮对在踏面上的蠕滑始终小于传统轮对，因此踏面磨耗也较小。

4 结论

通过对EDCW车辆系统动力学性能的分析可以得出以下结论：

（1）选择合适的耦合度时，EDCW车辆的动力学性能介于传统轮对与独立旋转车轮之间，在直线上其临界速度大于传统轮对，却无法超越独立旋转车轮；在曲线上的导向能力优于独立旋转车轮，弱于传统轮对。也就是说EDCW在直线上临界速度的提高是以在曲线上导向能力的下降为前提的。

（2）随耦合度从零逐渐增大，轮对逐渐从独立旋转车轮过渡到传统轮对，小耦合度时临界速度较高，大耦合度时导向性能较好，当耦合度足够大时，耦合轮对动力学性能与传统轮对相吻合。

（3）当耦合刚度或阻尼有一个取值较大时，另一个对系统动力学性能的影响甚微，只有二者取值均较小时，各自变化对系统的影响才较为明显。

（4）单纯的耦合阻尼不会引起EDCW系统的不稳定，而在小阻尼情况下，EDCW有较大的不稳定刚度区间，这种不稳定性随着耦合阻尼的增大而逐渐消失。

（5）EDCW轮缘磨耗大于传统轮对，而踏面磨耗小于传统轮对。

（6）为了更好地满足铁路发展需要，可以研制一种具有主动控制性能的耦合器，该耦合器的耦合度可以根据速度的变化而发生改变，高速时具有较小耦合度，低速和过曲线时具有较大耦合度。

［1］Ahmed A K W，Sankar S.Lateral Stability Behavior of Railway Freight Car System with Elasto-Damper Coupled Wheelset：part2-Truck Model［J］.Journal of Mechanisms，Transmissions，and Automation in Design.1987，109（12）：500-507.

［2］Ahmed A K W，Sankar S.Lateral Stability Behavior of Railway Freight Car System with Elasto-Damper Coupled Wheelset：part1-Wheelset Model［J］.Journal of Mechanisms，Transmissions，and Automation in Design.1987，109（12）：493-499.

［3］王开文，池茂儒.耦合轮对的发展［J］.铁道车辆，2002，40（12）：1-3.

［4］任 毅，李 芾，黄运华.独立旋转车轮动力学性能研究［J］.铁道机车车辆，2008，6（28）：15-19.

［5］李 芾，黄运华，傅茂海.车轮耦合方式发展及其导向机理［J］.机车电传动，2006，（2）：1-4，9.

［6］张丽平，李 芾.弹性阻尼耦合轮对铁路客车系统横向稳定性［J］.交通运输工程学报，2002，2（1）：13-19.