广义多载波调制解调滤波器组干扰分析

陈年泼，庄彦瑛，俞加伟，华惊宇

(浙江工业大学通信网应用技术研究省重点实验室，浙江杭州310023)

0 引言

随着移动通信和互联网技术的进一步融合，多载波技术由于其在提高频谱利用率、抵抗频率选择性衰落、支持多种不同业务等方面的天然优势，受到人们的广泛重视［1］。广义多载波正是在这样的背景下由FuTURE项目提出的新型宽带无线多址传输技术［2］。在2004年，有人研究了B3G系统中的GMC调制解调滤波器组设计和其快速应用［3］，并且也有人对MIMO-GMC系统的下行同步和硬件实现做了相关研究［4］。GMC应用方面做了相关的研究，通过GMC与CDMA的结合做了相应的研究工作［5、6］。传统的FMC系统采用217阶均方根升余弦(RRC)滤波器［7］，其在浮点意义上满足要求，但是它是否最优的选择，以及该滤波器的具体干扰性能并没有文献报道。这对于GMC的实际应用是不利的，因此本文从接收信号的时域表达式开始，引入滤波器组的影响，具体分析原型滤波器对于接收信号干扰性能的影响，为GMC的原型滤波器选用以及干扰分析提供参考。

1 GMC的信号模型与干扰分析

假设子带数量为M，在发送端的第k子带，输入信号yk(m)，N倍内插后为y'k(m)。经过子带发送滤波器hk(n)后，得到子带信号sk(n)。由于本文重点关注的是滤波器组对信号造成的ISI和ICI，可以假设信号经历的信道是恒等信道以简化分析，即c(n)=δ(n)，此时接收端有r(n)=s(n)。解调第k'子带，即r(n)经过子带滤波器gk'(n)后，得到y－k'(n)。基于滤波器组的GMC实现结构如图1所示。

根据图1可以得到如下子带输出表达式:

式2最后一个等号右边第一项包含了第k'子带信号的全部有用信息，第二项表示其他子带对第k'子带的干扰。事实上第一项还包含了ISI的影响，但是其和原型滤波器的形式有关，如果为严格意义上的奈奎斯特滤波器将不存在ISI，下面将对此作进一步分析。长度为L的原型滤波器其峰值响应前后各有D=(L－1)/2N个符号周期长度，因而过滤波器会有DN的时延，由综合/分析原型滤波器的系数一致性，接收端分析滤波器输出就会有2DN的时延。故N倍抽取后的滤波器输出'(m')解调应得到'(m'－2D)。对式2最后一个等号的右边第一项进行改写:

式3等号右边第一项是有用信号;第二项是第k'子带的所有其他采样点对当前样点的干扰，及ISI和ICI的和。假设单子带上符号互相独立，各子带上的符号也互相独立。不妨假设各子带各符号能量相等，即=E［|yk(m)|2］=1，计算最终接收端滤波器组的输出平均功率，即'(m')的平均功率:

式4等式右边第一项为解调增益，第二项为自干扰增益，第三项与第四项的和为子带间互干扰增益;它们都是相应平均功率与符号能量的比值。

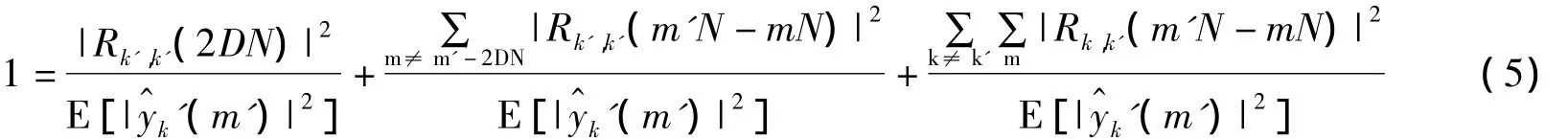
式5右边第一项为主值，第二项为ISI，第三项为ICI。至此，已经得到了ICI和ISI的闭合表达式。

2 数值结果分析

这里选择了3种不同的原型滤波器，对时域结果进行比较分析。在GMC的原型滤波器选择中，奈奎斯特滤波器［7－10］是最佳选择，然而有限长度下这是不可实现的。因此通常人们选用RRC滤波器，在过去GMC系统中，该滤波器的滚降因子α=0.22，采样率N=18，子载波数目M=16，延时2D=12。当实现均方根升余弦滤波器时，实际应用了两种窗函数，一种是用于控制过渡带宽的平滑连续函数，另一种是使脉冲响应限制在有限区间上的矩形窗函数。后者加剧了均方根升余弦滤波器频谱中的旁瓣效应，其原因在于半余弦过渡沿和阻带起点之间的边界上存在一阶不连续的导数，即在阻带的起始点处存在极大的不连贯性。而应用一种基于Remez算法的简单迭代算法，用于将低通滤波器转变为指定滚降系数的均方根升余弦频谱结构，并具有独立控制带通波纹和阻带波纹的能力，称为Nyq2滤波器。由于Nyq2滤波器在α=0.22时，最佳的延时2D=22，因此本文选择D=［3 4 5 6 10 11 12］作为示范。另外，本文亦调用matlab自带的remez函数设计一个低通滤波器作为对比。后面计算分析中的3种滤波器分别称为Nyq2，Rcosine和Remez。

2.1 干扰结果浮点计算分析

根据上述仿真条件得到的干扰结果的数据如表1所述。从表1可以看出，当滤波器阶数D取3，4，5，6时均方根升余弦滤波器在主值与ISI方面表现优于其他两种原型滤波器，特别是对ISI的压制效果明显。在D取较小的值时，适度增加D能显著地提高均方根升余弦滤波器组的性能，但是均方根升余弦滤波器对ICI的压制效果不佳，即使D持续增长，ICI也没有显著改善，始终保持在同一数量级上。这最终导致D的增长并不能显著地改善接收信号主值，提高信号的信干比。与此相反，用标准Remez法设计得到的原型滤波器对ICI的压制效果明显，在D取5时就达到了10－4这一量级。但它在ISI方面的表现不尽如人意，即使D取12，其ISI仍保持在1%以上。这导致了其信号主值并不能随着D的增长而有较大幅度的提高。若综合考虑ICI和ISI这两者的影响，均方根升余弦滤波器优于remez滤波器。另一方面，在ICI压制上，Nyq2滤波器较均方根升余弦滤波器更优;在ISI压制方面，Nyq2滤波器较标准Remez方法设计的滤波器更优。在D取值较小时，Nyq2的综合优势并不明显，在D取5或6时，其性能与均方根升余弦滤波器基本相当。如若继续增加D，Nyq2的优势开始凸现，原因在于Nyq2滤波器显著改良了滤波器旁瓣高度。最终当D取10时，Nyq2滤波器的总干扰已减少至10－5的量级，明显优于均方根升余弦滤波器和标准Remez滤波器。

表1 滤波器组时域性能比较浮点结果

3 结束语

在GMC调制解调滤波器组的实现结构上，进行时域干扰定量分析，得到了干扰和信号的闭合表达式。并以rcosine，Nyq2与Remez滤波器作为原型滤波器代入，进行浮点运算的比较分析。浮点结果显示，Nyq2作为原型滤波器的滤波器组，其时域主值会随着时延D的递增而逐步改善，最终优于Remez与rcosine。

［1］ 吴伟陵，牛凯.移动通信原理［M］.北京:电子工业出版社，2005:417－428.

［2］ Xiaohu Y，Guoan C，Gao M.Toward beyond 3G:the FuTURE project of China［J］.IEEE Communication Magazine，2005，43(1):70－75.

［3］ Han H，Xiqi G，Xiaohu Y.The Design of Generalized Modulated Filter Banks and its Fast Implementation in the B3G System［J］.Proc IEEE 6th CASSymposium.Emerging Technologies，2004，1(1):61－64.

［4］ 宋利.MIMO-GMC系统下行同步研究与硬件实现［D］.南京:东南大学，2007.

［5］ Giannakis G B，Wang Z，Scaglione A，et al.AMOUR—Generalized multi carrier transceivers for blind CDMA regardless of multipath［J］.IEEE Trans Commun，2000，48(12):2 064 –2 076.

［6］ Zhengdao Wang，Giannakis G B.Block precoding for MUI/ISI-resilient generalized multi carrier CDMA with multirate capabilities［J］.IEEE Transaction on communication，2001，49(11):2 016 －2 027.

［7］ Michael Joos.Theory of Root-Raised Cosine Filter［DB/OL］.Available:http://www.michael-joost.de/rrcfilter.pdf，2012－12－04.

［8］ Fredric JHarris，Chris Dick，Sridhar Seshagiri，et al.An Improved Square－Root Nyquist Shaping Filter［C］.California:Processing of the SDR 05 Technical Conference and Product Exposition，2005:130－135.

［9］ Jinno T，Saito Y，Okuda M.Advanced weighting scheme in the rational Remez algorithm for IIR digital filters［J］.Communications and Information Technologies，2010，1(1):579 －584.

［10］ Fredric JHarris.Multirate Signal Processing for Communication Systems［M］.New Jersey:Pearson Education，2004:236－253.