基于Bayesian准则的鲁棒自适应波束形成算法

杨 杰，李春晓，马永阳

(1.浙江工业大学信息工程学院，浙江杭州310023;2.浙江工业大学之江学院，浙江 杭州310024)

0 引言

一般情况下，研究波束形成算法的前提是知道确定的驾驶向量，即波达方向以及阵列是确定的［1、2］。但是，在实际的情况下，对于确切的驾驶向量是很难得到的，这时候就需要研究对于驾驶向量不确定的情况下的波束形成问题［3］。基于Bayesian方法的鲁棒自适应波束形成算法在驾驶向量不确定的情况下具有一定的鲁棒性。在高信噪比的条件下，Bayesian鲁棒波束形成算法能在期望信号处产生较高的增益，这样就会利于期望信号的提取;而在低信噪比的条件下，Bayesian鲁棒波束形成算法却能够使主波束展宽，这样的处理效果对于那些信源波达方向不确定的情况具有很好的宽容性。

1 Bayesian波束形成算法

Bayesian鲁棒波束形成算法是基于Bayesian准则的，所以在实际的应用中，假设信号波达方向θ是服从先验概率密度函数p(θ)的随机变量，这里的p(θ)反映了信号驾驶向量不确定性的程度。为了方便计算，假设p(θ)由P个离散点Θ=θ1，…，θp组成，则最小均方误差波束形成器的输出为:

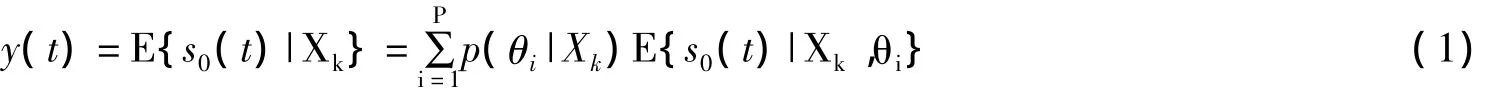
式中，s0(t)为期望信号，Xk为K次采样的阵列接收矩阵，p(θi|Xk)是角度θ的后验概率密度，即:

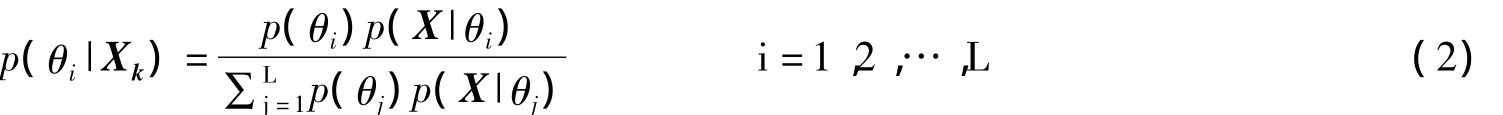
由矩阵求逆［4］及代入阵列接收矩阵等相关知识可以得到后验概率密度函数为:

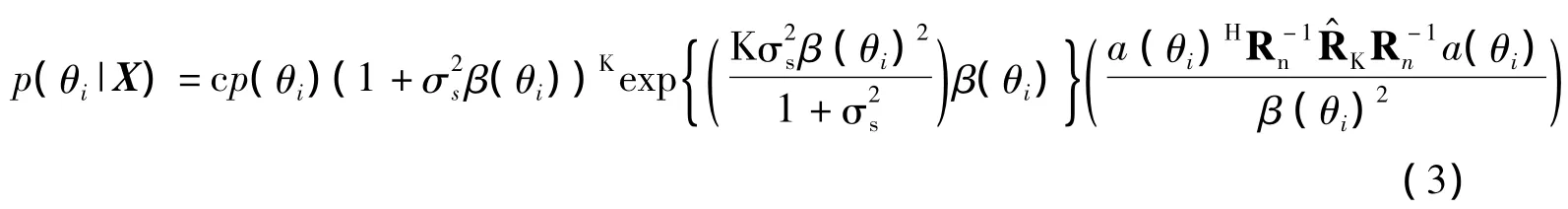
式中，c是一个独立于θi的归一化因子以保证概率密度函数的总和等于1。为了使波束形成器更有应用性，用来代替 RX，用)－1来代替。这样，Bayesian波束形成器将成为一个由后验概率密度函数加权的一系列自适应MVDR波束形成器的线性组合。但是，计算这个后验概率密度函数却是一个巨大的问题，由于式3是一个Rn的函数，所以这对于实际应用非常困难［5］。与其为了估计Rn而大大增加Bayesian波束形成器的复杂度，不如去寻找一个简单展开式，使它与后验概率密度函数近似。现定义:

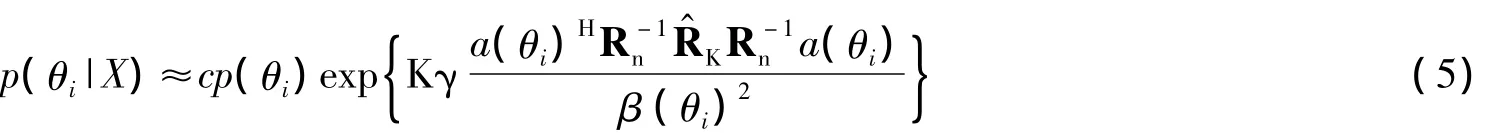
因为Rn是未知的，这里假设理想MVDR的权向量为:

那么，后验概率将近似等于:

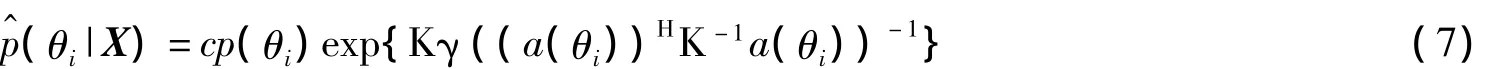
于是，得到Bayesian自适应波束形成器的权向量为:

2 仿真结果与分析

2.1 参数设置

在Bayesian波束形成器的仿真中，必须指定一些参数:采样快拍数K、常数γ、Θ中长度为L的离散波达方向的值、先验概率p(θ)以及对角加载值σ2。指定这些参数的值涉及到对波束形成器性能的权衡，最佳参数的设置由具体情况而定。

本文的仿真中，取10阵元均匀线阵，采样快拍数K=30，常数γ=0.6，干燥比INR=20dB，先验概率长度 L=6 且服从均匀分布，即 p(θi)=1/6，i=1，…，6。

2.2 仿真对比及分析

在上述的参数设置下，得到Bayesian波束形成器在不同信噪比及干扰的情况下的波束图和后验概率分布图如图1，2所示。

由图1可以看出，在高信噪比情况下，后验概率密度在真实信号方向附近有值，而在其他方向的后验概率趋于0，所以，Bayesian波束形成器能够准确地在真实波达方向附近形成波峰。在图2中，由于信噪比低以及干扰增多，波束形成器的一部分增益不会贡献到主波束的波峰上。此时，后验概率接近于先验概率的数值，这也恰好反映了由于信号环境恶劣，得到的数据很难提供关于驾驶向量的有用信息。Bayesian波束形成器在这种情况下就表现出了良好的鲁棒性能，凭借先验概率函数里的信息，能够在先验概率的范围内形成一个较宽的波束，来包容由于驾驶向量不确定而造成的偏差。

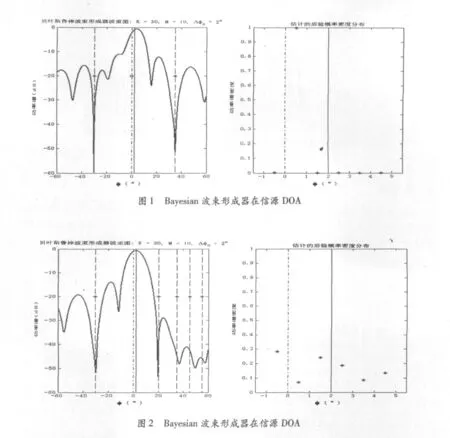
通过上述仿真对比，可以证明Bayesian波束形成器的性能，它能够综合观测数据及关于波达方向先验概率的知识，从而对驾驶向量不确定的情况具有很好的鲁棒性。在高低信噪比情况下，波束形成器后验概率分布有明显不同。可以看出，具有鲁棒性的波束形算法对驾驶向量不确定时的偏差具有较强的宽容性。

3 水声阵列实际数据校验

本文实际阵列模型为:阵列为32阵元均匀线阵，每个阵元间距为0.04m，水深1.44m，目标距离9.0m，目标深度0.83m，声音在水中的传播速度为1 500m/s。为了简化计算，把模型设定为远场的情况，即信号到各阵元的延迟忽略不计。由此可以很快计算出信号的实际入射角度为1.209 4°。

如图3所示，鲁棒算法能够较好地形成一个拥有主瓣的波束，并且主瓣波峰对应的角度正是实际目标的波达方向(可能由于数据长度、采样点数等因素影响会有微小误差)，验证了Bayesian鲁棒波束形成算法的有效性。通过实际水声阵列数据的仿真，搭起了一座理论与实际相联系的桥梁［6］。

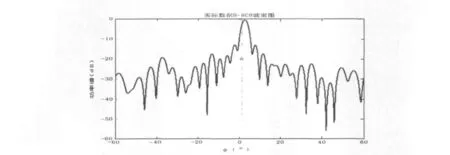
图3 基于实际数据的Bayesian鲁棒波束形成算法仿真图

4 结束语

综上所述，基于Bayesian准则的鲁棒波束形成算法在驾驶向量不确定的情况下具有一定的鲁棒性。本文通过仿真对比了波束形成器在不同信噪比及干扰的情况下的性能，验证了该波束形成算法的理论。最后，还通过水声阵列实际数据来校验该算法的有效性，得到较为满意的结果。

［1］ 杨维，陈俊仕，李世明.移动通信中的阵列天线技术［M］.北京:清华大学出版社，2005:16－20.

［2］ PrasadA S，Vasudevan S，Selvalakshmi R.Analysis of adaptive algorithms for digital beamforming in smart antennas［J］.Recent Trends in Information Technology，2011，3(5):64 －68.

［3］ Lin G，Li Y A，Jin B L.Research on the algorithms of robust adaptive beam forming［J］.Mechatronics and Automation，2010，4(7):751 －755.

［4］ 张贤达.矩阵分析与应用［M］.北京:清华大学出版社，2004:112－128.

［5］ Am leh K，Li HB.Robust channel estimation and detection for single-carrier and multicarrier block transmission systems［J］.Vehicular Technology，2010，59(2):662 －672.

［6］ Chang L N.A robust adaptive beam former for high-rate underwater acoustic communication systems［J］.Underwater Technology，1988，15(17):493 －498.