表面张力对微挤出流场的影响

傅志红，陈玉辉，肖雄辉

（中南大学机电工程学院，湖南 长沙410083）

0 前言

挤出成型因为具有实用范围广、生产效率高、投资少、见效快等一系列优点而成为高聚物成型的最重要的方法之一。近年来，产品微型化呈现出蓬勃发展的趋势。挤出产品也朝着微型化的方向发展。由于微尺度效应［1-2］的影响，宏观的工艺参数、结构参数、物理参数不能简单的按几何比例缩小应用到微挤出成型过程中。一些在宏观挤出中可以忽略的影响因素包括壁面滑移、表面张力、对流换热、黏性耗散等在微尺度效应下变得不可忽略［3-9］，甚至成为影响微挤出成型的主要因素。对塑料熔体在微型通道内的流变行为［10-11］的研究是对流变理论的一种完善和补充，有助于推动微挤出的不断完善，并且有利于扩大塑料微挤出技术的应用领域。

本文采用Polyflow软件对聚合物在微通道中的流变行为进行数值模拟，研究了表面张力对微挤出流场的影响。

1 表面张力

1.1 定义或解释

促使液体表面收缩的力叫做表面张力，其本质是分子力，是液体表面层由于分子引力不均衡而产生的沿表面作用于任一界线上的张力。表面张力的方向和液面相切，其合力沿着曲面法向方向。接触角用来表示表面张力的方向。表面张力及接触角如图1所示。

单位面积上的表面张力的合力fn使表面曲率减少，σ为表面张力系数，满足式（1）：

图1 表面张力及接触角Fig.1 Surface tension and contact angle

式中 fn——单位面积上的法向力，N／m2

σ——表面张力系数，N／m

R——材料接触界面的高斯曲率，m

n——液体自由表面法向方向的单位矢量

R 满足式（2）：

式中 R1、R2——接触界面的2种材料的曲率半径

表面张力的方向和液面相切，液体表面由于表面张力作用所引起的切向力为：

式中 fτ——液体表面上受到的切向力

l——自由表面的长度

τ——液体自由表面切向方向的单位矢量

通常用接触角（θ）来描述切向力的方向。以水平线为参考线，逆时针为正，顺时针为负：

在计算流体力学中，常采用Brackbill的连续表面力模型CSF［12］将界面的表面张力项离散为等效的体积力，以附加体积力的方式加到流体的动量方程中。它分布在交界面上很薄的一层区域内。其离散公式为：

式中 k——界面上的曲率

δ（x）——界面上的函数

n——界面上的法向向量（向外为正）

δ（x-xs）——狄拉克δ函数

xs——界面S上的点

2 数值模拟

采用聚合物专用流体分析软件Polyflow，对圆形截面的流道进行模拟分析，探讨表面张力的尺寸效应及表面张力系数和接触角对微挤出流场的影响。由于流道结构及流场的对称性，本模拟采用轴对称分析。模拟分析的流道尺寸及网格划分如图2所示。微通道尺寸AE＝4×AB＝1.2mm。网格采用四边形结构单元。节点数量为3751，网格数量为3600。

图2 微通道的网格Fig.2 Mesh of micro channel

在数值模拟时，熔体自由表面在模拟的过程中会发生变形，自由表面的网格会因为自由表面位置的变化而发生变化。此时，需要采用网格重置技术。网格重置可以根据边界点的位置的变化重新定位内部网格节点。Spine法是一种比较简单，适用于二维挤出成型的网格重置方法。其网格节点是沿着线性进行重新组织的，如图3所示。节点的位置确定是按照一维方式进行逻辑排列的，这就像是对二维平面进行切片，切片的方式是沿着自由表面或者移动边界的法向方向，从而得到最终的网格。Spine法是线性组织的，并且在每个线段的端点处都有相应的节点。假设x1、x2是线段的2个端点。按照Spine法的规则，内部节点的位移数学表达式为：

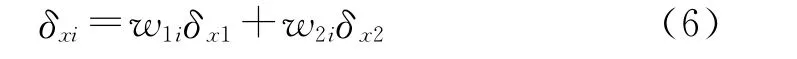
其中，δx代表一个方向总的位移量，w1i、w2i为权重：

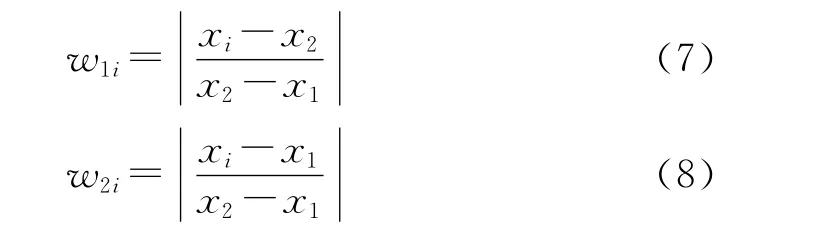
图3 Spine法变形网格Fig.3 Deformation mesh of Spine

塑料熔体的表面张力系数一般在50N／mm左右，模拟时表面张力系数的取值范围为（0～50N／mm），接触角取值范围为（-50°～50°）。材料黏度模型采用常数η0＝100Pa·s。边界条件设定为：EF为材料进口端，法向速度设置为10mm／s，BF为对称轴，CE壁面处的速度为零，AB边界设置为法向力等于零，切向力等于零，AC为自由表面。

3 模拟结果分析与讨论

AE＝1.2mm时，表面张力系数为零和表面张力系数为50N／mm时的网格变形如图4所示。从图4可以看出，有表面张力和没有表面张力的时候，网格的变形并没有太大的区别，只是网格的变形量略微有些不同。说明有表面张力的时候，自由表面的形变方式并没有很大的变化。但在自由表面出口处的变形非常明显。这说明表面张力对微挤出自由表面出口处的流场影响很大。这是因为自由表面出口处的边界条件突然变化，从而导致表面张力在此处的作用效果有较大变化。

图4 网格变形图Fig.4 Deformation of mesh

3.1 表面张力的尺度效应及对挤出胀大的影响

在本文的模拟分析中，为了确定表面张力的尺度效应及对挤出胀大的影响，接触角为零时，分别取AE为1200、120、12、1.2mm，表面张力系数值为0～50N／mm。数值模拟计算得到的挤出胀大比值（自由表面变形前后最大半径之比）如图5所示。

由图5可知，通道尺寸越小，挤出胀大效应越明显。这是因为通道尺寸越大，熔体惯性力起主导作用，黏性力和表面张力可忽略不计。通道尺寸越小，黏性力和表面张力的作用效果越明显。当通道尺寸达到毫米级和微米级时，表面张力对挤出胀大的影响变得显著。而且表面张力系数增大，挤出胀大比值也越大，其关系大致呈线性关系。这是因为在熔体表面张力的作用下，熔体受到向外的径向分力，从而使得表面向外膨胀，表面张力系数值变大，这种向外的分力也就越大。因此材料的挤出胀大比值随着表面张力系数的变大而变大。表面张力对自由表面的径向分力为：

φ——自由表面变形前后夹角

自由表面变形前后夹角φ跟挤出胀大比值有关，在自由表面变形前后夹角φ值变化不大的情况下，自由表面所受的径向力和表面张力系数几乎呈线性关系。

为了方便研究表面张力在微挤出中的影响，本文以下模拟均在AE为1.2mm的情况下进行。

3.2 接触角对挤出胀大的影响

表面张力系数为50N／mm时，接触角取值：-50°～50°。数值模拟计算得到的挤出胀大比值如图6所示。

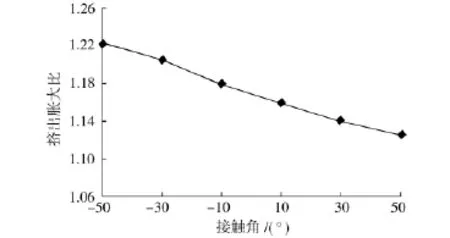
图6 接触角对挤出胀大的影响Fig.6 Influence of contact angle on extrusion swelling

由图6可知，表面张力系数不变时，挤出胀大比值随着接触角的增大而减小，这是因为在自由表面出口处，接触角对自由表面的作用产生很大影响，自由表面出口处的表面张力对自由表面的径向分力为：

在接触角由负值增大的过程中，表面张力对自由表面出口处向外的径向分力越来越小，因此自由表面的挤出胀大作用越来越小。

3.3 表面张力和接触角对口模内熔体压力场及速度场的影响

接触角为零时，表面张力系数值取0～50N／mm。模拟得到的口模内熔体压力场与速度场如图7所示。从图7（a）可以看出口，模内熔体进出口压力降随着表面张力系数的增大略微有些减小，由图7（b）、（c）、（d）可知，口模内熔体进口压力与出口压力以及口模出口处的熔体平均速度都随着表面张力系数的增大而增大。图7（a）中熔体压力降减小说明材料在口模流动过程中的能量损失减小。这是因为表面张力对流体的轴向分力对流体有牵引作用，如：

图7 表面张力系数对口模压强与速度的影响Fig.7 Influence of surface tension coefficient on pressure and velocity of extrusion die

在表面张力系数从零增大到50N／mm过程中时，表面张力对口模出口处的流体牵引力增大，使得流体在流动过程中与壁面的剪切所导致的能量损失减小，而能量损失的大小与口模进出口压力降的大小是直接相关的。所以压力降略微减小。图7（b）、（c）中口模平均进口压力和口模平均出口压力的增大说明在表面张力的作用下，自由表面对口模内的流体有很大的阻力。这是因为表面张力在挤出膨胀过程中做负功，流体的能量损失加大，表面张力增大，挤出膨胀增大，从而能量的损失增大，因此，口模进出口压强增加。图7（d）中熔体平均出口速度略微增大，是因为在口模出口处，表面张力对流体有一个径向的分力，径向力的大小如式（7）所示，径向分力始终为正值，使得平均径向出口速度增加。而轴向速度由于进口速度不变而不变，因此总的速度略微增加。而没有表面张力和有表面张力时速度有较大的变化，这是因为考虑挤出胀大后，动量方程中加了表面张力项，相比没有表面张力的动量方程出现一定的变化，使得计算出现较大的变化或者由于口模出口处的网格变形使得数值模拟的结果偏离原来的计算点。由于在口模出口处流场的变化较大，网格的微小变形都会导致较大的误差。

在表面张力系数为50N／mm不变时，接触角取值：-50°～50°。得到口模压力降、口模平均进出口压力、以及口模出口平均速度曲线如图8所示。由图8可知，接触角与口模流场参数的关系并不是线性关系。由图6可知接触角θ增大，自由表面挤出胀大比值减小，φ减小，表面张力对口模出口处的轴向分力如式（9）所示，牵引力随着夹角φ值的减小而增大，使得材料在口模内的剪切能量损失减小，因此压力降减小。所以图8（a）中口模平均进出口压力降减小。而图8（b）、（c）中口模内熔体进出口压强的减小是因为挤出胀大减小，自由表面对外做功减小，自由表面对口模的阻力减小。图8（d）中口模平均出口速度减小是因为表面张力对自由表面的径向分力减小，口模内熔体出口径向速度减小，而熔体轴向速度不变，因此平均速度减小。

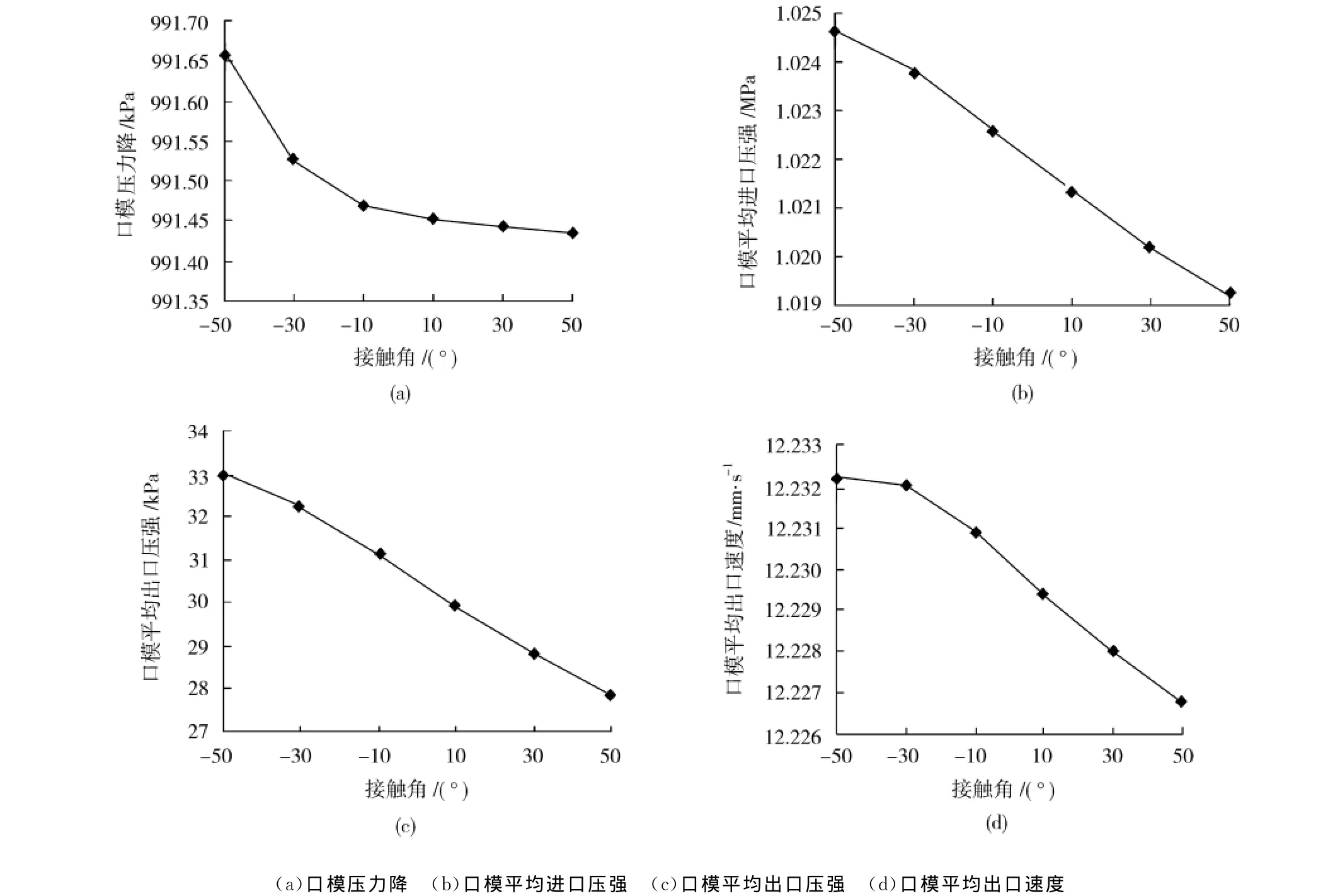
图8 接触角对口模压强与速度的影响Fig.8 Influence of contact angle on the pressure and velocity of extrusion die

3.4 表面张力和接触角对熔体自由表面压力场与速度场的影响

图9 表面张力系数对自由表面出口压强与速度的影响Fig.9 Influence of surface tension coefficient on pressure and velocity at the exit of free face

接触角为零时，表面张力系数值取0～50N／mm，计算得到的熔体自由表面出口处压强与速度如图9所示。图9（a）中表面张力系数为零时，自由表面出口处的压力值接近零但并不等于零，是因为材料的黏度比较大，在自由表面出口附近流体之间产生的小的剪切作用使得流体在自由表面出口处的压力值不为零。表面张力在自由表面流动负方向的切向分力为：

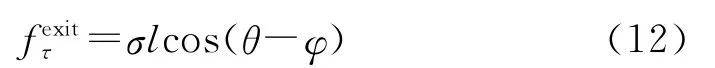
接触角与自由表面变形前后夹角φ基本不变时，切向分力随着表面张力系数的增大而增大，因此负压增大。图9（b）中自由表面平均出口速度减小是因为越大的负压阻碍流体的流动。

表面张力系数取50N／mm，接触角取值为-50°～50°时得到的自由表面出口压强与自由表面出口平均速度曲线如图10所示。

图10 接触角对自由表面出口压强与速度的影响Fig.10 Influence of contact angle on pressure and velocity at the exit of free face

由图10可知，自由表面出口负压随着接触角的增大先增大后减小。这是因为表面张力对自由平面出口切线分力如式（10）所示，自由表面变形前后夹角φ约为-20°，因此，当接触角θ约为-20°时，所受的负切向分力最大，因此导致自由表面出口压强在此处为极值。而随着接触角的增大，挤出胀大减小，在进口速度不变时，自由表面出口面积较小，因此出口速度增大。

4 结论

（1）在挤出过程中通道尺寸减小，表面张力对挤出胀大比值的影响增大，当尺寸达到毫米级和微米级时，表面张力成为影响挤出胀大比值主要因素之一；

（2）在微挤出中，表面张力系数越大，挤出胀大越明显，挤出口模内熔体的进出口压强都明显增大，口模内熔体的压力降略微减小，平均出口速度略微增大，自由表面出口压力与平均出口速度都明显减小；

（3）接触角由负值到正值变化时挤出胀大比值减小，挤出口模内熔体的进出口压强明显减小，熔体的压力降与平均出口速度略微减小，自由表面出口负压先增大后减小，自由表面平均出口速度增大。

［1］蒋炳炎，谢 磊，吴旺青，等.微尺度流道中流体流动前沿的喷泉流动仿真［J］.高分子材料科学与工程，2006，（5）：5-9.Jiang Bingyan，Xie Lei，Wu Wangqing，et al.Simulation of Fountain Flow for Micro Channel Fluid Front［J］.Polymer Materials Science and Engineering，2006，（5）：5-9.

［2］Hetsroni G，Mosyak A，Pogrebnyak E，et al.Fluid Flow in Micro-channels［J］.International Journal of Heat and Mass Transfer，2005，48（10）：1982-1998.

［3］Zhao D，Jin Y，Wang M，et al.Experimental Study and Molecular Dynamics Simulation of Wall Slip in a Micro-extrusion Flowing Process［J］.Proceedings of the Institution of Mechanical Engineers，Part C：Journal of Mechanical Engineering Science，2011，225（5）：1175-1190.

［4］石建军，成志强，柳葆生.微注射成形中表面张力效应的数值模拟［J］.应用力学学报，2010，（4）：727-731.Shi Jianjun，Cheng Zhiqiang，Liu Baosheng.Numerical Analysis to Surface Tension Effects of Micro-injection Molding［J］.Chinese Journal of Applied Mechanics，2010，（4）：727-731.

［5］于同敏，李又民，徐 斌.微注塑成型充模流动中的表面张力［J］.高分子材料科学与工程，2009，（12）：153-157.Yu Tongmin，Li Youmin，Xu Bin.Surface Tension in Filling Flow of Micro Injection Molding［J］.Polymer Materials Science and Engineering，2009，（12）：153-157.

［6］Golovnev I F，Golovneva E I，Fomin V M.Molecular-dynamical Study of Surface Tension in Nanostructures［J］.Mechanics of Solids，2010，（3）：343-351.

［7］Saksono P H，PeriĉD.On Finite Element Modeling of Surface Tension：Variational Formulation and Applications—Part II：Dynamic Problems［J］.Computational Mechanics，2005，（3）：251-263.

［8］Kim D S，Lee K C，Kwon T H，et al.Micro-channel Fill-ing Flow Considering Surface Tension Effect［J］.Journal of Micromechanics and Microengineering，2002，12（3）：236-246.

［9］Bochkarev A，Hartman M，Olson K，et al.Limitations of Classical Methods for Measuring Surface Tension in Viscoelastic Liquids［J］.Journal of Coatings Technology and Research，2009，（3）：347-353.

［10］Chen C，Chen S，Liaw W，et al.Rheological Behavior of POM Polymer Melt Flowing Through Micro-channels［J］.European Polymer Journal，2008，44（6）：1891-1898.

［11］Liang J Z.Effects of Extrusion Conditions on Die-swell Behavior of Polypropylene／Diatomite Composite Melts［J］.Polymer Testing，2008，27（8）：936-940.

［12］Brackbill J U，Kothe D B，Zemach C.A Continuum Method for Modeling Surface Tension［J］.Journal of Computational Physics，1992，100（2）：335-354.