多模噪声及其消噪研究

孙万麟

(1.昌吉学院物理系,中国 昌吉 831100；2.新疆大学信息科学与工程学院,中国 乌鲁木齐 830046)

非高斯噪声的研究已经成为现代信号处理的核心问题之一，一般采用高阶统计量方法进行研究。但是，高阶统计量方法存在计算方差大、算法比较复杂和实时性差的缺点，而小波包变换能够避免高阶统计量存在的缺点,利用小波包变换良好的时频分析特性，对信号和噪声进行频谱分析，通过把频带进行多层次划分，并根据被分析信号的特征，自适应的选择相应频段，使之与信号频谱相匹配，从而提高时频分辨率，实现了强噪声背景下的信号提取。

文献[1～2]表明，对非高斯噪声做小波包变换，随着非高斯噪声序列长度的增加或分解尺度的增多，在此子空间上将产生近似高斯分布的输出．因为多模噪声[3]是非高斯噪声，因而小波包变换能够用于分析多模噪声．

1 多模噪声[3]模型

(1)模型1：高斯过程g(t)迭加震荡过程，其概率密度函数为：

(1)

其中，σ2是高斯分量的方差，Bi是第i个振荡信号的振幅，θi是第i个振荡信号的相位．

(2)模型2：高斯过程g(t)加码间干扰(ISI)过程，其概率密度函数为

(2)

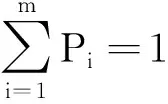
(3)模型3：当bi>2σ时，模型2的概率密度函数可写成如下形式(模型2的特例)：

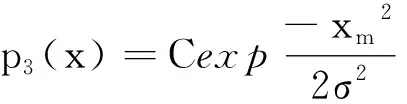
(3)

其中，xi=xi-1-bisignxi-1，i=1,…,m，signx为符号函数．

2 小波包变换

(1)小波包分解算法：

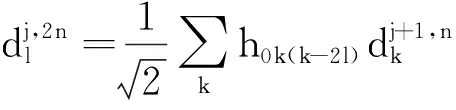
(4)

(5)

(2)小波包重构算法：

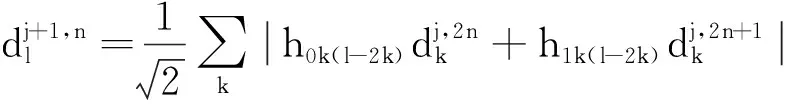
(6)

3 小波包变换处理多模噪声

本文采用db20小波函数[4-7](dbN 小波基非常适合于将信号正交地分解到各独立频带内，实现对非平稳信号的整体刻画，是通用非平稳信号分析工具)和shannon熵对多模噪声序列作小波包变换，分解尺度为3，样本长度为1×108，在尺度3上的偏态系数和峰态系数值如表1所示.

表1 模型1 (Bi=2.5)

表2 模型2 (bi=1.5)

表3 模型3 (bi=3)

将表1～3数据与正态分布的偏态系数0和峰态系数3进行比较可知，对多模噪声序列做小波包变换，其尺度3上的小波包子空间变换系数都近似于高斯分布．也就是说，多模噪声的模型变化，不影响小波包子空间变换系数对多模噪声高斯化的性能．

4 仿真及其分析

为了研究方便，本文以工程中经常碰到的余弦信号为激励信号(也称为被测信号或确知信号)，假设待检测确知信号为S(t)=Acos(2π×180 0t)，采用db20小波函数和shannon熵对夹杂以下各种噪声的余弦信号情况做小波包分解[8-11]，分解尺度为3，样本长度为1×108，仿真结果如图1和图2所示．

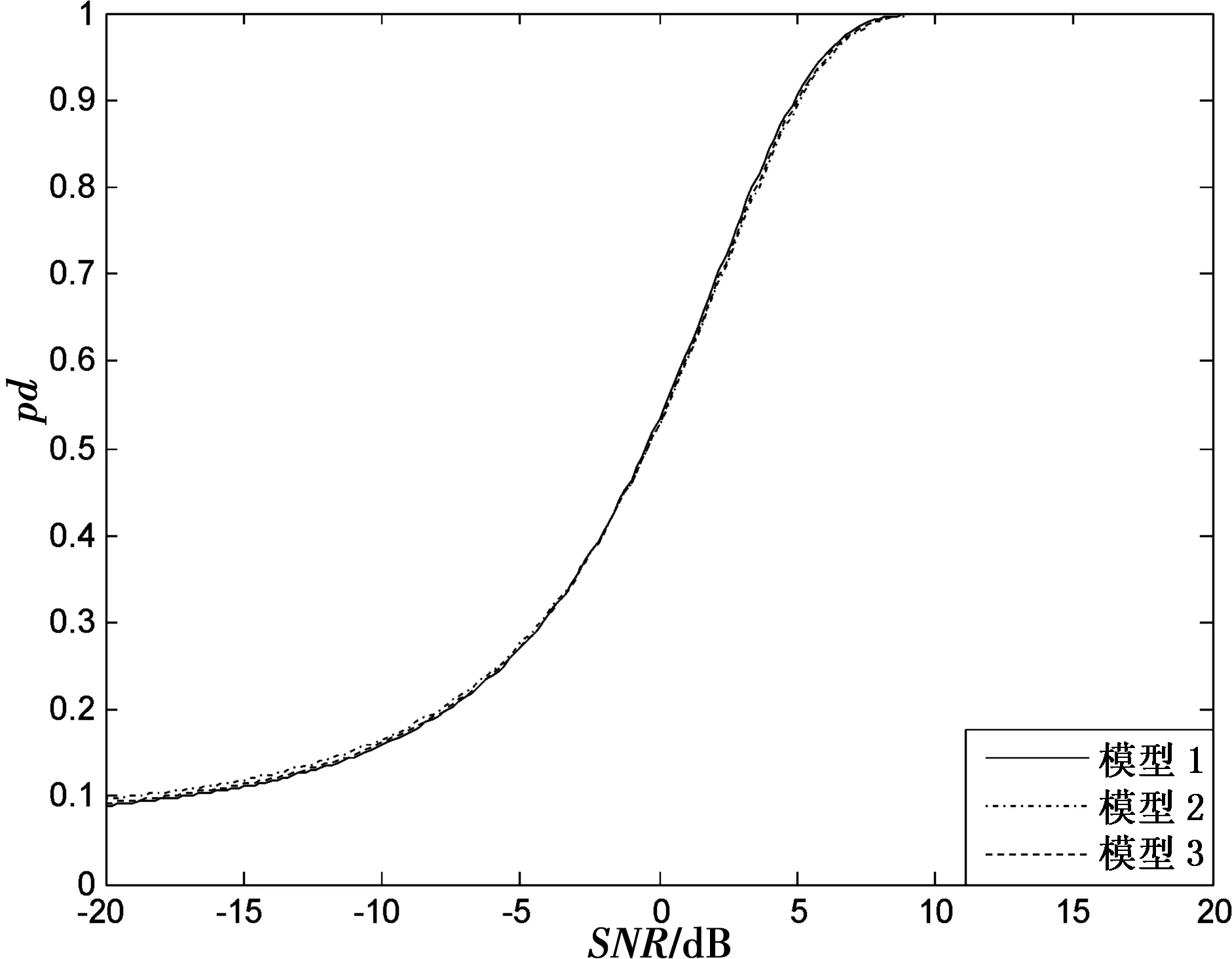
图1 3种简化多模噪声背景下的小波包检测性能曲线比较

图2 两种噪声背景下的小波包检测性能曲线比较

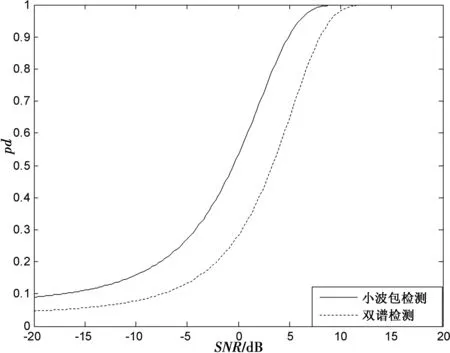
图3 模型2背景下的两种检测系统性能曲线比较

由图1可知，3种模型的多模噪声通过小波包变换检测系统后检测性能非常接近. 但由图2可知，多模噪声(模型2)背景下的小波包检测性能曲线跟高斯噪声背景下的小波包检测性能曲线相比，随着信噪比增大，两种检测性能曲线慢慢靠近，最后直接重合.因此，在相对较大信噪比条件下, 通过对多模噪声做小波包变换，可以实现将复杂的多模噪声转化为高斯噪声来处理．

为了证实小波包变换检测系统在多模噪声背景下检测性能的改善，本文把待检测确知信号S(t)=Acos(2π×1 800t)夹杂多模噪声(模型2)分别通过小波包变换检测系统和传统高阶统计量(双谱)检测系统[12-13]进行仿真比较，如图3所示．

由图3可知，在多模噪声(模型2)干扰下，小波包变换检测系统比双谱的检测性能高，而且在相对信噪比很低条件下就有信号检测功能．

5 结论

本文通过仿真比较，证实了小波包变换检测系统在多模噪声背景下检测弱信号的可行性，比传统的高阶统计量方法优越.因为多模噪声是非高斯噪声，所以本文研究的方法，适用于非高斯噪声，具有一定的参考价值．

参考文献：

[1] 林 蓉.小波包变换用于非高斯噪声下的信号检测[D].成都:电子科技大学,2005.

[2] 向 前,林春生,龚沈光.基于小波包变换的非高斯噪声信号结构分析[J].电子与信息学报, 2004,26(1):60-64.

[3] 山拜·达拉拜,黄玉划.多模噪声理论及其在通信保密中的应用[J].电讯技术,2008,48(2):20-24.

[4] 王国秋、杨梦云.双正交小波的谱半径及其应用[J]. 湖南师范大学自然科学学报，2011,34(1):14-18.

[5] 张汝波,林佳仕,李学耀.基于小波系数统计的非高斯噪声背景下语音流检测[J].哈尔滨工程大学学报, 2004,25(4): 487-490.

[6] STEVEN M K.统计信号处理基础—估计与检测理论[M].罗鹏飞,张文明,刘 忠,等译．北京:电子工业出版社,2006.

[7] 飞思科技产品研发中心. MATLAB7辅助信号处理技术与应用[M]. 北京：电子工业出版社，2005.

[8] FRANCOIS C B, DAVID R. Constructive action of additive noise in optimal detection[J]. Int J Bifurc Chaos,2005,15(9): 2985-2994.

[9] 王首勇,朱光喜,唐远炎.应用最优小波包变换的特征提取方法[J].电子学报,2003(7)：1305-1308.

[10] 丁 浩,黄志尧,李海青.基于高阶统计量和小波变换的差压信号分析[J].浙江大学学报：工学版,2006,40(4): 714-718.

[11] 苗 峰,赵荣珍.小波消噪和盲源分离在转子故障信号分析中的应用方法[J].河南科技大学学报：自然科学版,2008,29(6):14-17.

[12] DORON K, HAGIT M. Suboptimal detection of non-gaussian signals by third order spectral analysis[J].IEEE Trans Assp,1990,38(6): 901-909.

[13] 杨晨阳,屈剑明,李少洪,等．高阶统计量在检测中的应用[J].信号处理,1995,11(4): 288-294.