一类变分包含组解的强收敛定理
2012-11-22冯世强何中全
史 杰,冯世强,何中全
(西华师范大学数学与信息学院,中国 南充 637009)
设E是Banach空间,E*是其对偶空间,正规对偶映射J:E→2E*如下定义:
J(x)=f∈E*:〈x,f〉=‖x‖2=‖f‖2,x∈E,
其中,当E是严格凸的光滑的Banach空间时,J和J-1是单值的[1].
设E是光滑的Banach空间,函数φ:E×E→R如下定义:
φ(x,y)=‖x‖2-2〈x,Jy〉+‖y‖2,∀x,y∈E.
由于〈x,Jy〉≤‖x‖‖Jy‖=‖x‖‖y‖,于是(‖x‖-‖y‖)2≤φ(x,y),即φ(x,y)≥0.
设E是严格凸且光滑的自反Banach空间,C是E中非空闭凸集.那么对任意的x∈E,存在唯一的x0∈C使得[1]
φ(x0,x)=minφ(y,x),y∈C.
本文称x0是x在C上的投影.定义投影算子∏C:E→2C如下
∏C(x)=y∈C:φ(y,x)=minφ(z,x),z∈C,x∈E.
设E是Banach空间,E*是其对偶空间,集值映射M:E→2E*,若满足
〈x-y,f-g〉≥0,∀x,y∈E,f∈Mx,g∈My,
则称M是单调的.若M满足
(1)M是单调的;
(2)对(x,f)∈E×E*,〈x-y,f-g〉≥0,∀y∈E,g∈My,必有f∈Mx.
则称M是极大单调的.
设E是Banach空间,E*是其对偶空间.若映射T:E→E满足
φ(Tx,Ty)≤〈Tx-Ty,Jx-Jy〉,∀x,y∈E,
则称T为确定非扩张的.易得,T为确定非扩张的等价于
〈Tx-Ty,JTx-JTy〉≤〈Tx-Ty,Jx-Jy〉,∀x,y∈E.
若映射B:E→E*满足
(1)η:E→E为任意一个确定非扩张映射;
(2)对任意λ≥0,有
〈η(J-1(Jx-λBx))-η(J-1(Jy-λBy)),Bx-By〉≥0,∀x,y∈E.
则称B为广义单调的.显然,广义单调映射必是单调的.
设Bi:E→E*是单值映射,Mi:E→2E*是多值映射,i=1,2,…,N,θ是零元素.本文研究如下的变分包含组问题(VISP):
VISP 求x∈E,使得
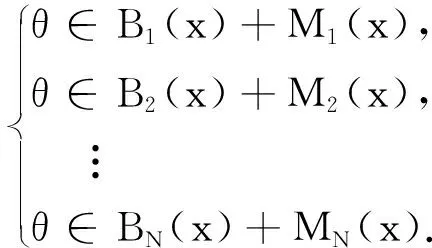
当Bi≡B,Mi≡M,VISP问题变为如下变分包含问题(Ⅵ):
VI 设B:E→E*是单值映射,M:E→2E*是多值映射,θ是零元素,求x∈E,使得θ∈B(x)+M(x)成立.

下面给出本文所需的一些引理.
引理1[2]设M:E→2E*是极大单调映射,B:E→E*是Lipshitz连续映射,则S=M+B:E→2E*是极大单调映射.
引理2[1]设E是严格凸的光滑实自反Banach空间,C是E中非空闭凸集,令x∈E,那么对任意y∈C,有φ(y,∏Cx)+φ(∏Cx,x)≤φ(y,x).
引理3[3]设E是严格凸的光滑实Banach空间,xn、yn都是E中子列,xn或yn是有界的且
φ(xn,yn)→0,n→∞,那么有xn-yn→0,n→∞.
引理4[1]令C是一光滑实Banach空间E凸集,令x∈E,那么x0∈∏Cx当且仅当
〈z-x0,Jx0-Jx〉≥0,∀z∈C.
1 主要结果
本节将通过构造非扩张映射,得到新的迭代算法,使之产生的序列收敛到变分包含组问题的解.本文工作推广和改进了文献[2]、[4~10]中的一些结果.

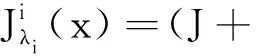
其中Mi:E→2E*是极大单调映射,Bi:E→E*是Lipshitz连续映射,λi>0.


即
再由Mi的极大单调性得

(1)
又由于φ(z2,z1)+φ(z1,z2)≥0得
0≤‖z2‖2+‖z1‖2-2〈z2,Jz1〉+‖z1‖2+‖z2‖2-2〈z1,Jz2〉=2(‖z2‖2+‖z1‖2-
〈z2,Jz1〉-〈z1,Jz2〉)=2(〈z2,Jz2〉+〈z1,Jz1〉-〈z2,Jz1〉-〈z1,Jz2〉)=2〈z2-z1,Jz2-Jz1〉.
即
〈z2-z1,Jz2-Jz1〉≥0.
(2)

引理6设E是Banach空间,E*是其对偶空间,对一切i=1,…,N,∀x∈E,有下面结论成立:
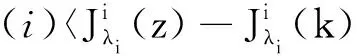



对任意x,y∈E,由Mi的极大单调性得


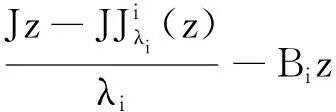

由Mi的极大单调性得


即






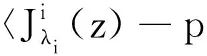
因此

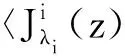
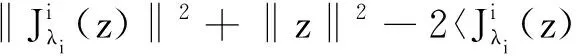





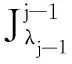

证毕.
接下来构造如下算法W:

其中,0≤ηn≤e对任意0≤e<1,i=0,1,…,n.

证分4步来证明.



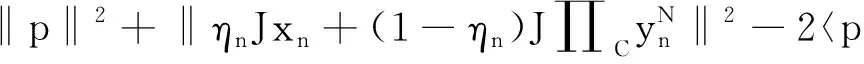
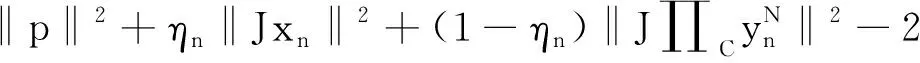
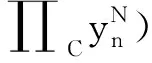
(3)


由于xn=∏Cn(x0),根据引理2,得
φ(xn,x0)≤φ(p,x0)-φ(p,xn)≤φ(p,x0),φ(xn,x0)≤φ(xn+1,x0),∀n≥0.
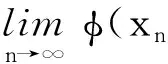
φ(xn+m,xn)=φ(xn+m,∏Cn(x0))≤φ(xn+m,x0)-φ(xn,x0).






故有


2‖p‖‖Jzn-Jxn‖).
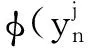


任取(vj,gj)∈Bj+Mj,即gj-Bj(vj)∈Mj(vj).由Mj的极大单调性得
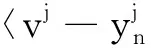
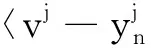





参考文献:
[1] ZEGEYE H, ERIC U, OFOEDU E U,etal. Convergence theorems for equilibrium problem, variotional inequality problem and countably infinite relatively quasi-nonexpansive mappings[J].Appl Math Comput, 2010,216(12):3439-3449.
[2] KUMAM W, JAIBOON C, KUMAM P,etal. A shrinking projection method for generalized mixed equilibrium problems, variational inclusion problems and a finite family of quasi-nonexpansive mappings[J/OL]. http://dx.doi.org/10.1155/2010/458247,2010-03-21/2010-06-29.
[3] KAMIMURA S, TAKAHASHI W. Strong convergence of proximal-type algorithm in a Banach space[J].SIAM J, 2002,13(3):938-945.
[4] ZHANG S S, LEE J W, CHAN C K. Algorithms of common solutions to quasi variational inclusion and fixed point problems[J].Appl Math Mech, 2008,29(5):571-581.
[5] ZHANG S S, LEE J W, CHAN C K. Quadratic minimization for equilibrium problem variational inclusion and fixed point problem[J]. Appl Math Mech, 2010,31(7):917-928.
[6] 曹 珂.一类非线性三阶三点边值问题单调正解的存在[J].湖南师范大学自然科学学报,2011,34(4):13-17.
[7] LIN L J, WANG S Y, CHUANG C S. Existence theorems of systems of variational inclusion problems with applications[J].J Glob Optim,2008,40(4):751-764.
[8] KRISTALY A, VARGA C. Set-valued versions of Ky Fan’s inequality with application to variational inclusion theory[J].J Math Anal Appl,2003,282:8-20.
[9] DING X P, LAI T C, YU S J. Systems of generalized vector quasi-variational inclusion problems and application to mathematical programs[J].Taiwanese J Math,2009,13(5):1515-1536.
[10] DING X P. Systems of generalized quasi-variational inclusion (disclusion) problems in FC-spaces[J]. Appl Math Mech, 2010,31(5):545-556.
[11] JITPEERA T, KUMAM P. A new hybrid algorithm for a system of mixed equilibrium problems, fixed point problems for nonexpansive semigroup, and variational inclusion problem[J/OL].http:dx/doi.org/10.1155/2011/217407,2010-12-14/2011-01-15.
[12] LIOU Y C. An iterative algorithm for mixed equilibrium problems and variational inclusions approach to variational inequalities[J/OL]. http://dx.doi.org/10.1155/2010/564361,2009-09-13/2010-01-10.
[13] TAN J F, CHANG S S. Iterative algorithms for finding common solutions to variational inclusion equilibrium and fixed point problems[J/OL]. http://dx.doi.org/10.1155/2011/915629,2010-10-30/2010-11-09.
