时序数据故障点检测方法分析比较及应用

2012-11-22贺力克

湖南师范大学自然科学学报 2012年2期

贺力克

(湖南工业职业技术学院电气工程系，中国长沙 410208)

时序数据是一种服从某分布的随机变量，在不同时刻有一个取值，并按照时间发生的顺序排列而成的统计序列．随机变量的分布主要用分布函数参数如均值、方差等来表示．当形成时序数据的一系列随机变量，由于某种条件的变化而不再服从之前的分布，则称该时间序列发生了故障(有文献称之为“变点”、“孤立点”等)．故障点的检测在各个领域得到了广泛的应用．在一个时序数据中，利用已有信息对下一秒是否异常点并给出合理的估计和警报的类型，是现代故障检测和故障容错领域的热点研究问题[1]；采用这种方法也能有效的检测图像中隐藏的信息，检测计算机网络是否收到病毒或者黑客的攻击．基于此类广泛的应用，故障点的检测算法已在统计学界得到了广泛的研究．

目前对时序数据的分析方法主要包括两种类型：数理统计方法和数据挖掘方法[2]．数据统计方法是通过统计学中的模型假设、参数估计、模型检验等手段获取描述时序数据的规律．数据挖掘方法则从时间序列局部特性出发，从大量的、不完备的、有噪声的数据中，提取隐含在其中的一些规律[3]．早在1995年Nikiforov就提出了异常点检测模型用于检测和避免时间序列中突发的变化[4]．目前学者们已经开发了大量的孤立点检测算法，可以分为三类：基于模型的技术[5]、基于临近度的技术[6]和基于密度的技术．王建州等人[5]指出排除时序数据中故障点能使故障点对时序数据的影响变小，但是可能导致重要的隐藏信息的丢失．为了解决此类问题，提出了一种统计分析结合小波变换的方法．文献[7]结合密度和临近度的概念，提出了一种基于引力的孤立点检测方法，通过考虑数据周围的密度和数据对象间的距离等参数对孤立点定义的影响来挖掘数据集中隐含的孤立．此外，小波变换具有自动改变窗长的功能，可以很好地把信号在空间和频率上局部化，这以特性使得小波变换对信号的变点分析也有一席之地[8]．

对国内外文献调查分析发现，研究学者针对不同的时序数据，提出了很多时间序列变点的检测方法，每种方法都是针对某一种情况有着较好的检测效率，然而并没有对常见的检测算法进行行之有效的对比．本文旨在对几种主要的时间序列的故障点检测算法进行性能分析，为其他研究者在选取基于数理统计和分线性序列分析两种基本检测方法时提供一些参考．

1 时序数据基本模型

在变点检测问题中，有一系列的观测值(观测样本)，多数情况下，观测值按其垂涎时间的先后排序．在某个位置时刻，样本的分布或其他数字特征起了突然的变化，这个时刻就是变点．也有可能样本分布依赖于某种空间参数，而变点则是空间中的位置或时间轴上的某一时刻．设x1，x2，…，xn是相互独立的随机变量，并且服从某种分布．通常xi可以表示成如下形式

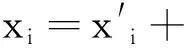
(1)

假设在一个未知的时刻t时，ξ(i)的值为ξ(t)=ξ0；而到下一个时刻t+1时，ξ(i)的值为ξ(t+1)=ξ1．因此式(1)描述了带有异常点时间系统的一般模型，ξ0表示了对于系统F而言正常的状态，而ξ1表示一系列非正常状态(故障、变点)．假设系统F的输出值表示为x1，x2，…，xn，变点检测即检测和尽量地避免ξ(i)的非正常变化，例如从ξ0状态变为ξ1．

根据上述离散时间系统的一般模型，本文讨论的在某未知时刻t+1时发生的故障ξ1简化表示为

2 几种孤立点检测方法分析

2.1 基于引力的孤立点检测算法

这种孤立点检测算法主要借鉴了牛顿万有引力的思想，考虑将数序数据看作是n个质量均匀的点，不均匀地分布在数据空间中，每个数据对象的影响可以用一个引力函数来表示[7]．依据时序数据点对临近时刻数据的引力函数的大小来作为判断孤立点的标准．具体的引力函数如下式所示

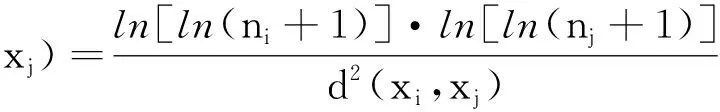
其中d(xi,xj)表示数据对象xi与xj的距离；ln[ln(ni+1)]表示数据点i的质量；ni表示数据xi在距离d内的邻居数．这里用ln[ln(ni+1)]表示第i个数据点的质量，是为了避免密度较大的数据点相乘使得引力急剧增大而出现“黑洞”现象，算法过程参见文献[7]，这里不再赘述．

但是从此类算法的本质来看，处理序列时间数据具有一定的局限性．通常来说时序数据是连续性的一维数据，定义相邻数据点的方法也比较单一，不能放在一个多维向量中来考虑，必须采取有效的分段才能处理分段时序数据[9]，而且此类处理方法通常用于图像等维数较多的数据处理[10]．针对此类问题，学者们专门研究了时序数据变点的检测算法．

2.2 基于均值变点的检测算法

文献[11]研究了一般情况下均值变点检测模型，如式(1)所描述的一般系统模型．取一个位置或时刻i，考察i附近的局部内样本均值或样本和的变化，即指定一个适当的自然数d，把i左右的各d个观测值(一般称d为步长或窗口长度)求和并相减，得

yi=(xi+…+xi+d-1)-(xi-d+…+xi-1).

(2)

其中i=d+1,d+2,…,n-d+1，若i非变点并且与变点位置t+1的距离不小于d，则上式右边两项有相似的均值且yi趋近于0；反之若当前检测点i等于t+1或离t+1很近，则式(2)左右两项的均值不同，yi趋远于0．

该变点检测算法对步长d的选择具有较大的依赖性，若d选取过小，对观测值的变化会过于敏感；反之若d选取过大，会使随机误差的影响削弱，对误差的呈现不敏感．文献[11]对d的取值给出了一个估计方法，本文中不再做讨论．但是在对d的估计过程中，须已知所有观测值样本的总数n，然而这对于在线变点检测是一个瓶颈．

2.3 基于均值方差变点估计的孤立点检测

文献[12]研究了独立序列中均值与方差变点的估计问题，作者考虑了序列的均值和方差是否有变点的情况．

设序列{xt|t=1,…,T} 满足E(xn)=μ(t)， Var(xn)=σ(t) ．若μ(t)，σ(t)取值分别为μ1、μ2和σ1、σ2，且有

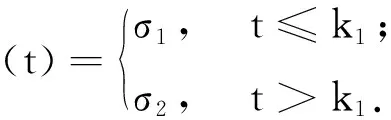
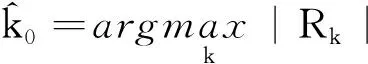
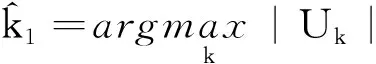
其中

上述变点估计问题只是针对一个序列中存在单一变点的情况，对于多变点的情况作者并没有考虑，然而时序数据中变点的多发性是必然的，因此这也是该检测算法的一个缺陷．

3 GPS采集数据的模拟试验与实例分析

本节用实际采集的GPS数据作为模拟研究和分析的源数据，用于对比文章中提到的3种基于时序类型的变点检测方法，而采用文献[8]中提到的小波检测结果作为真实结果．GPS接收机可以采集到导航坐标系中东向、北向和天向3个方向的速度，然而GPS接收机在运动过程中可能会收到系统误差、机器误差、噪声的影响而对采集到的数据产生数据变点，准确估计变点发生的位置或时间对数据下一步的使用有着重要的意义．本文在测试算法性能过程中采用了一组GPS接收数据来评价几种检测方法的性能，限于篇幅原因，仅选取两个方向进行分析，原始数据图见图1(a)，(b)．

(a) GPS接收机采集到的东向速度原始数据 (b) GPS接收机采集到的北向速度原始数据图1 GPS接收机采集到的东、北向速度原始数据

测试数据的样本容量为6 906，即T=6 906，采样频率为10 Hz．从图1中看出数据是部分平稳的，发生了较多的跳变，需要采用变点检测算法对其进行变点检测，确定变点的位置．

(a) 东向速度“引力”检测结果 (b) 北向速度“引力”检测结果图2 基于引力的孤立点检测结果

图2(a)，(b)所示为基于引力的孤立点检测算法对GPS东北向速度采样数据的修正结果，检测结果见表1．可以看出在前半段修正后的结果比采样结果有较大的偏差，后半段较小．表1中也可以看出检测变点数目比其他两种方式都小，可见该检测算法发生了误检和漏检．这与该算法的理论基础有关，定义该“虚拟引力”的概念有些牵强．不能很好地解释数据中发生变点的内在原因[13]．

图3和图4为另外两种基于统计模型的变点检测方法．图中有3条线，分别代表误差、误差估计上阈值、误差估计下阈值．超过估计阈值的时刻则检测为变点，在区间内的则表示正常数据时刻．在处理这两个类似检测算法时，作者对GPS采样数据进行了一阶差分操作，接着对查分序列进行变点检测．从表1中可以看出“均值变点检测算法”和“均值方差变点检测算法”的检测效率和结果不相上下．相比较而言，图3中所示的均值变点检测方法算法较为简单，因此计算代价比较小，而图4中的均值方差变点检测方法需要检测观测数据序列的两种统计量的变化，因此计算消耗的代价较大，而性能没有得到太大的提高．

(a)东向速度均值变点点检测结果 (b)北向速度均值变点点检测结果图3 均值变点检测结果

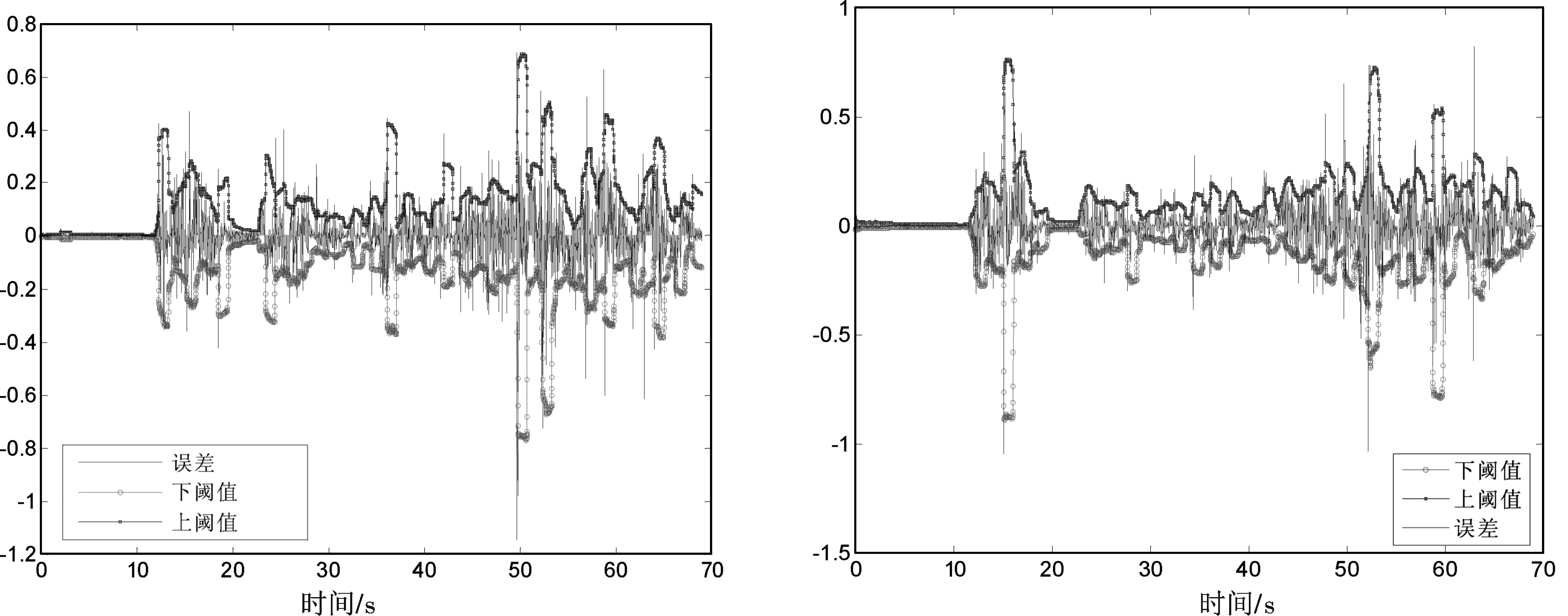
(a)东向速度均值方差变点点检测结果 (b)北向速度均值方差变点点检测结果图4 均值方差变点检测结果

由以上的模拟研究和实例分析来看，本文精确地比较了几种变点检测算法的性能，每种检测算法均能较好地判断变点的个数并准确地估计变点发生的时刻，采用变点检测算法之前需要确定的较重要的参数为步长，该参数较大地影响了变点检测算法的效果．此外，基于“引力”的孤立点检测算法由于其理论性不强的缘故，检测效率和其他两种算法略有差别．而其他两种检测算法在检测性能上不相上下，只是算法代价有差别．

表1 3种检测算法检测率的比较

4 结束语

本文比较了3种不同的序列故障点检测算法，分别是：基于“引力”的孤立点检测算法，基于“均值变点”的检测算法和基于“均值方差变点估计”的检测算法．分别对这3种算法进行了分析比较，并从试验的角度对3种算法进行了性能评价．试验以GPS接收机实测的东北天3个方向的速度数据为基础，最后给出了检测结果和性能结果．试验表明：基于“引力”的孤立点检测算法效果不如其他两种算法，而基于“均值变点”的检测算法在计算代价上又优于基于“均值方差变点估计”的检测算法．本文的工作能为选取变点检测算法时提供有价值的参考．

参考文献：

[1] 程瑞琪,周美玉.基于统计与时间序列的内燃机车机油光谱数据分析与故障诊断[J]. 铁道学报,1999,21(4):20 -24.

[2] 刘齐宏，李大德，周志斌,等.基于RFaD与基因表达式编程的经济统计时序挖掘[J]. 四川大学学报：工程科学版,2008,40(5):121-124.

[3] 苏圣超,张正道,朱大奇.基于时间序列数据挖掘的旋转机械故障预报[J].南京航空航天大学学报,2006,38(1):121-123.

[4] NIKIFOROV I. A generalized change detection problem[J]. IEEE Trans Inf Theor, 1995, 41(1): 171- 187.

[5] 王建州,杨勇.基于统计分布的小波分析对时间序列孤立点数据的识别与挖掘[J]. 西北师范大学自然科学学报,2004,40(2):3-6.

[6] 孙焕良,鲍玉斌,于戈,等.一种基于划分的孤立点检测算法[J].软件学报，2006, 17(5):1009-1016.

[7] 孟建良,姚亮, 程伟想.基于引力的孤立点检测算法[J].计算机应用与软,2009, 26(1): 254-257.

[8] 齐培艳,田铮,段西发,等.噪声为单位根过程的非参数函数变点的小波检测[J]. 控制理论与应用,2009,26(1):57-61.

[9] 刘合兵,尚俊平. 基于距离和密度的聚类和孤立点检测算法[J]. 河南师范大学自然科学学报,2008,36 (3):38-40.

[10] 马捷,严家斌,刘贵忠,等.混合噪声的各向异性扩散平滑[J].中南大学自然科学学报,2010,41(1): 213-237.

[11] 王晓原,隽志才,朴基男,等.局部比较的变点统计理论及其在交通流突变研究中的应用[J]. 公路交通科技,2002,19(6):112-115.