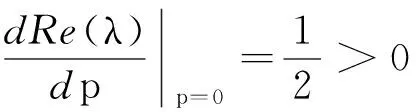带有避难项的扩散捕食模型的稳定性及Hopf分岔
2012-11-22李成林
李成林
(1.保山学院数学系, 中国 保山 678000; 2.西南大学数学与统计学院, 中国 重庆 400715)
带有常数避难项的ODE食饵捕食模型如下[1-9]:
du/dt=αu(1-u/K)-β(u-m)v/(1+a(u-m)), (x,t)∈Ω×(0,T),
dv/dt=-bv+(u-m)v/(1+a(u-m)), (x,t)∈Ω×(0,T),
(1)
其中Ω是Rn(n≥1是正整数)中具有光滑边界∂Ω的有界区域;u和v分别表示食饵和捕食者密度;正常数b,K,α,β,m分别代表捕食者的死亡率,食饵的环境容纳量,食饵的内禀增长率,传化率,避难常数;u/(1+au)是功能Ⅱ型反应函数. 根据生态学意义,当u≤m时,(u-m)/(1+a(u-m))=0.
对具有避难项的ODE捕食系统已有很多研究.文献[2]考察了系统(1)的平衡点稳定性并证明极限环的存在性.Hassel[3]在没有避难项的模型基础上增加一大的避难项,得到稳定性的结果完全不同.McNair[7]证明了除了避难项能阻止捕食食饵的震荡性外,它还具有合理的出入口动力学行为.在文献[10]中, Huang指出增加避难项能增加食饵密度.直到现在,食饵避难被广泛认为能阻止食饵灭绝和捕食食饵震荡.对于避难项更多的生物背景和研究结果,可参考文献 [1,6,9,11-12]等.但对于带有常数避难项的反应扩散系统的研究还不多见.
捕食者和食饵的相互作用能产生丰富的动力学行为[13],空间结构能进一步影响两物种的动力学行为.对于反应扩散捕食系统的研究,不同的物种是否能共存是人们最感兴趣的问题之一.很多情况下,物种在定态解处能共存,其中常数平衡解就是其中的一类定态解.常数平衡解的稳定性研究是种群生态学的一个中心研究课题,它能揭示种群未来的生活状况[13-15].
这篇文章的主要目的是研究具有常数避难项的反应扩散捕食系统常数平衡点的稳定性及Hopf分支.即研究下列反应扩散系统常数平衡解的稳定性及分支:
∂u/dt-d1Δu=αu(1-u/K)-β(u-m)v/(1+a(u-m)), (x,t)∈Ω×(0,T),
∂v/dt-d2Δv=-bv+(u-m)v/(1+a(u-m)), (x,t)∈Ω×(0,T),
∂u/∂v=∂v/∂v=0, (x,t)∈∂Ω×(0,T),
(u(0,x),v(0,x))=(u0(x),v0(x)),x∈Ω,
(2)
其中Ω是Rn(n≥1是正整数)中具有光滑边界∂Ω的有界区域;u和v分别表示食饵和捕食者密度;正常数d1和d2是相应种群的扩散系数;其他系数与模型(1)中的相同.
本文证明了(2)的动力学行为依赖于避难常数m. 对模型(2)的稳定性我们考虑局部和全局稳定性,得到当避难常数充分小时,正常数平衡点是全局渐近稳定的,当避难常数m满足条件K-b/(cβ-ab) 模型(2)有3个非负常数平衡点:(0,0),(K,0)和(u*,v*). 正常数平衡点(u*,v*)只有当cβ>ab及0 显然,当m>K-b/(cβ-ab)时,模型(2)不存在正常数解. 设0=μ0<μ1<…<μk<…→+∞是-Δ在Ω中齐次留曼边界条件下的特征值且ψ是相应的特征函数. 定理1模型(2)的平衡解(0, 0)是不稳定的. 证在(0,0)处模型(2)线性化方程为 wt=(DΔ+Fw(0,0))w, 其中 w=(u(t,x),v(t,x)), 通过计算得 考虑下面的特征值问题 λ是DΔ+Fw(0,0)的特征值当且仅当λ是矩阵-μkD+Fw(0,0)(k≥1)的特征值.利用文献[15]中特征函数张量(2.6)式: 考察(0,0)处的局部稳定性,只需考虑特征多项式 det(λI+μkD-Fw(0,0))=λ2+B1λ+B2, 其中 存在正整数N使得当k≤N时,d1μk-α<0,从而定理得证. 证通过直接计算得 证通过直接计算可得 u(T1,x)>0,x∈Ω. 应用比较原理,可得 (3) v(T1,x)>0,x∈Ω. (4) 由比较原理得 (5) 由(3)和(5)可得 因此,(K,0)是稳定的. (x,t)∈Ω×[T1,∞), u(T1,x)>0,x∈Ω. (6) 又利用比较原理可得 (7) 即(K,0)吸引了(2)的每一个解. 因此,(K,0)是渐近稳定的. 其中 则对t>T有 其中 因此有 因此有E′(t)≤0,其中只有当(u,v)=(u*,v*)时等号才成立.证毕. 对正常数解(u*,v*)处的Hopf 分支,算子DΔ+Fw(u*,v*)必定有共轭纯虚数.根据定理3的证明,不稳定区域只有当 才能发生. 应用[16]中的Hopf分支定理可得下列Hopf分支结果: 参考文献: [1] COLLINGS J B. Bifurcation and stability analysis of a temperature-dependent mite predator-prey interaction model incorporating a prey refuge[J]. Bull Math Biol, 1995,57(1):63-76. [2] GONZALEZ-OLIVARES E, RAMOS-JILIBERTO R. Dynamic consequences of prey refuges in a simple model system: more prey, fewer predators and enhanced stability[J]. Ecol Model, 2003,166(1):135-146. [3] HASSEL M P. The dynamics of arthropod predator-prey systems[M]. Princeton:Princeton University Press, 1978. [4] HOLLING C S. The functional response of predators to prey density and its role in mimicry and population regulations[J]. Mem Entomol Soci Canad, 1965, 45(1):3-60. [5] KAR T K. Stability analysis of a prey-predator model incorporating a prey refuge[J]. Commun Nonlinear Sci Numer Simul, 2005, 10(6):681-691. [6] KAR T K. Modelling and analysis of a harvested prey-predator system incorporating a prey refuge[J]. J Comput Appl Math, 2006, 185(1):19-33. [7] MCNAIR J N. Stability effects of prey refuges with entry-exit dynamics[J]. J Theoret Biol, 1987, 125(3):449-464. [8] MCNAIR J N. The effects of refuges on predator-prey interactions: a reconsideration[J]. Theoret Popul Biol, 1986, 29(1):38-63. [9] SIH A. Prey refuges and predator-prey stability[J]. Theoret Popul Biol, 1987,31(1):1-12. [10] HUANG Y J, CHEN F D, LI Z. Stability analysis of a prey-predator model with Holling type III response function incorporating a prey refuge[J]. Appl Math Comput, 2006,182(1):672-683. [11] KRIVAN V. Effects of optimal antipredator behavior of prey on predator-prey dynamics: the role of refuges[J]. Theoret Popul Biol, 1998, 53(2):131-142. [12] 戴求亿,顾永耕,刘 芳.半线性抛物方程的一个门槛结果[J].湖南师范大学自然科学学报,2011,34(6):7-15. [13] MURRAY J D. Mathematics biology Ⅱ: spatial models and biochemical applications[M]. 3rd ed. New York: Springer, 2003. [14] FAN Y H, LI W T. Global asymptotic stability of a ratio-dependent predator-prey system with diffusion[J]. J Comput Appl Math, 2006, 188(2):205-227. [15] KO W, RYU K. A qualitative study on geneal Gause-type predator-prey models with non-monotonic functional response[J]. Nonlinear Anal RWA, 2009, 10(4):2558-2573. [16] CRANDALL M G, RABINOWITZ P H. The hopf bifurcation theorem in infinite dimensions[J]. Arch RationalMech Anal, 1977, 67(1):53-72.
1 平衡点的稳定性
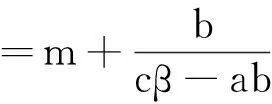

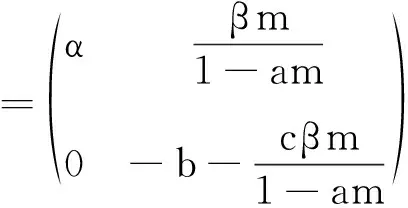
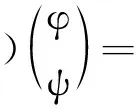
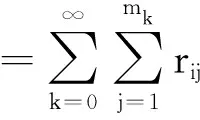
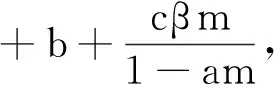


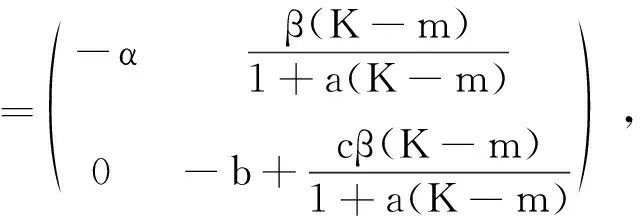

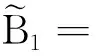



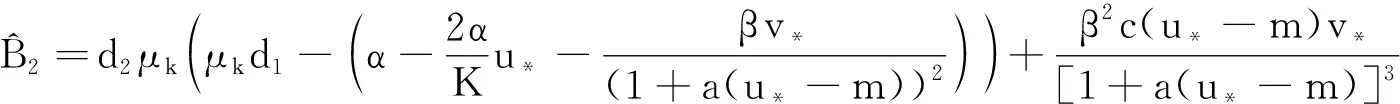
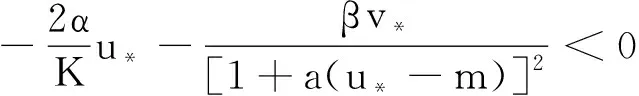

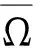

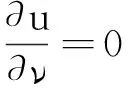
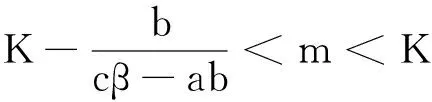
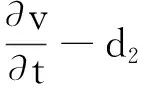
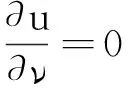
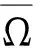
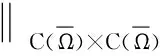
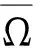

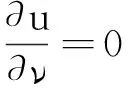

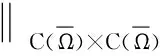
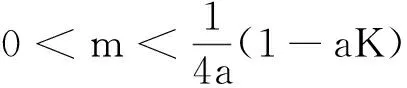
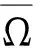

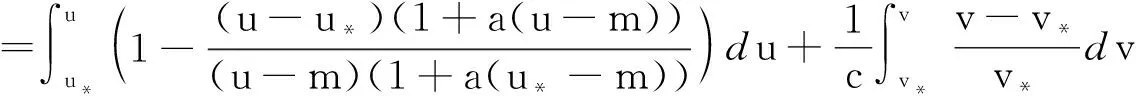



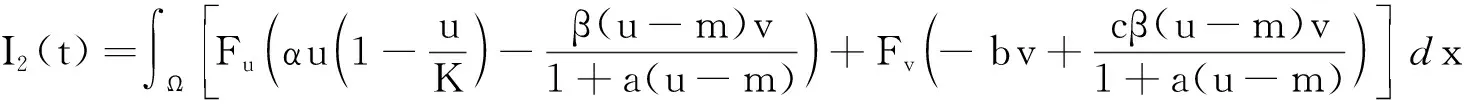

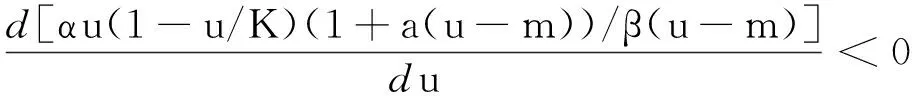

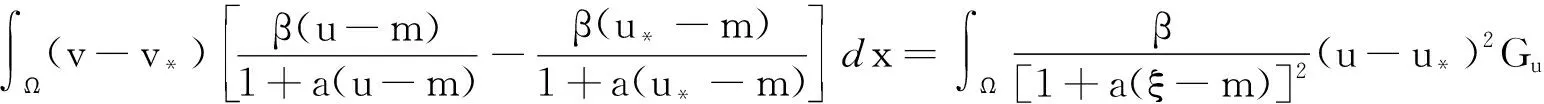
2 Hopf 分支