一对姊妹不等式猜想的证明

●吴裕东( 新昌中学浙江新昌312500)

●胡努春( 浙江师范大学数理与信息工程学院浙江金华321004)

一对姊妹不等式猜想的证明

●吴裕东( 新昌中学浙江新昌312500)

●胡努春( 浙江师范大学数理与信息工程学院浙江金华321004)

文献[1]在文献[2]和[3]的基础上证明了不等式(1)当n=3 时的情形，并提出了如下一对有趣的姊妹不等式猜想．

猜想1若x1,x2,…,xn∈R+(n≥3,n∈N*),且x1+x2+…+xn=1,则

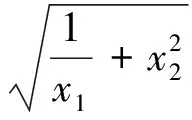
猜想2若x1,x2,…,xn∈R+(n≥3,n∈N*),且x1+x2+…+xn=1,则

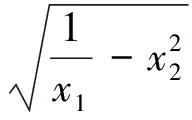
本文给出这2个不等式猜想的证明.首先给出不等式(1)的证明.

证明由x1,x2,…,xn∈R+,x1+x2+…+xn=1和均值不等式可得

即

(x1x2…xn)-1≥nn.

再由均值不等式得

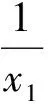
同理可得

…

于是

故不等式(1)得证.

下面给出不等式(2)的证明.

证明(1)当n≥4时，由x1,x2,…,xn∈R+,x1+x2+…+xn=1和均值不等式可得

(2)当n=3时,由x1,x2,x3∈R+,x1+x2+x3=1和均值不等式可得

故当n=3时,不等式(3)亦成立,从而对一切n≥3(n∈N*),不等式(3)都成立.同理

…

又当n≥3(n∈N*)时,n6-2n5-2n4+2n3-4=n4(n+1)(n-3)+n4+2n3-4>0,于是

从而

不等式(2)得证.

对不等式(2),令n=3,即得文献[1]提出的另一个猜想.

推论1若x1,x2,x3∈R+,且x1+x2+x3=1,则

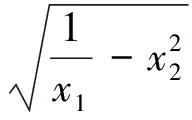
根据不等式(1)和(2),笔者提出更一般的一对姊妹不等式猜想:

猜想3若x1,x2,…,xn∈R+(n≥2,n∈N*,p,q∈N*),且x1+x2+…+xn=1,则

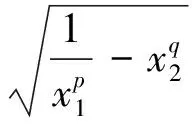
（6）

[1]李永利,刘真真.一对姊妹不等式的联想[J].数学通讯,2010(6):40.

[2]有名辉.一个不等式的另证及推广[J].数学通讯,2009(18):24-25.

[3]夏开平.一对优雅的姊妹不等式[J].数学通讯,2008(19):27.