新课程教学需要让学生先行,教师断后
——一节高三复习课的教学实录及感悟
2012-11-20杭州市第九中学浙江杭州310020
● (杭州市第九中学 浙江杭州 310020)
新课程教学需要让学生先行,教师断后
——一节高三复习课的教学实录及感悟
●缪荷芳(杭州市第九中学 浙江杭州 310020)
高三数学课以复习课为主,为了达到复习效果,应突出重点,攻克难点,加深学生对数学知识的理解,渗透数学思想,提高学生的思维能力,培养学生的创新意识和探究意识,调动学生学习的积极性,体现新课程中自主、合作、创新的基本精神.教师在课堂上要改变原有的教学模式,为了达到这个目的,笔者作了多方尝试,以下是笔者亲身经历的一节课的课例,具体如下:
1 课例实录
1.1 复习引入
教师:(幻灯片)回忆:确定一条直线需要几个条件?哪几个?
学生七嘴八舌,教师根据学生所说整理出其中的要点,并板书:

1.2 新课讲解
接着笔者给出了这节课的问题:
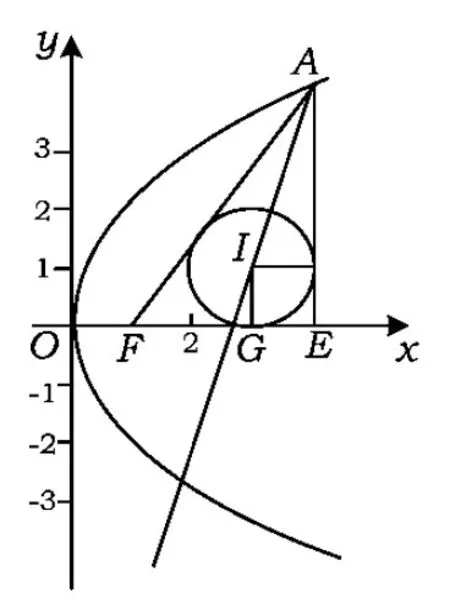
例1如图1,已知抛物线C的对称轴为x轴,且过点A(4,4),F为其焦点,E为点A在x轴上的射影.
(1)求抛物线C的标准方程;
(2)求∠FAE的角平分线所在的直线l的方程(请至少用2种方法求解).
(2010年安徽省数学高考文科试题第17题改编)
先让学生在讲义上自己完成,然后笔者在巡视过程中叫了2位学生到黑板上各板演一种解法,其余学生不受影响继续考虑.
板演学生给出了如下2种解法:

图1

图2
学生1:如图2所示,利用角平分线上点到角的2边距离相等这一性质求解.
设∠FAE的角平分线为l,l与x轴交于点G(x0,0),则
|GE|=4-x0(1 直线AF所在的直线方程为 解得 因此所求直线的方程为3x-y-8=0. 学生2:利用两角和的正切公式求解. 设∠FAE=2θ,角平分线l与x轴交于点G,设GE=x,则 解得 于是 由两点式可得所求直线的方程为3x-y-8=0. 教师:此解法是否可以优化? 学生3:可以.设∠FAE=2θ,则 解得 则所求直线的斜率为3,由点斜式得所求直线的方程为3x-y-8=0. 图3 教师:是否还有其他解法? 此时,学生争先恐后要发表自己的见解. 学生4:如图3所示,利用向量的夹角求解. cos∠FAG=cos∠EAG, 得 代入解得 则所求直线的方程为 3x-y-8=0. 学生5:可利用角平分线的性质求解. 学生6:如图4所示,可利用角平分线的性质求解. 图4 也可利用FH与平分线垂直,直接利用斜率积为-1求得. 学生7:如图5所示,利用三角形的内心求解. 由于△AEF是直角三角形,求得Rt△AEF的内切圆半径为1,则内心I的坐标为(3,1),由两点式可求得所求直线的方程为3x-y-8=0. 图5 图6 笔者环顾四周,发现已经没有其他解法. 笔者提示:能不能将前面的解法进行优化,就像刚才黑板上的解法2一样.对于解法4,主要是看点G,能否用直线的方向考虑呢? 教师:此题所求的是直线方程,又已知直线上一个点,因此再探求另一个点或直线的方向即可确定直线.前面我们已经得到了好几种点的情况,下面能否从方向的角度去考虑,比如解法2与刚才的解法都是求方向的,再看看还有没有其他方法(从方向的角度). 环顾片刻,学生没有反应. 教师:提示:要知道直线AG的方向向量,除了用刚才的方法之外,我们还可以用向量的线性运算来得到,如2个向量相加. 教师边说边在图上提示得到图6. 图7 教师:又由题意可知这个四边形是什么四边形? 教师边讲边在图上画出图6中的小圆圈提示.通过引导,给出了图7.此时学生也得到了以下解法: 从而所求直线的斜率k=3,故所求直线的方程为3x-y-8=0. 1.3 课堂小结 笔者根据学生的回答总结出解决上述问题的基本思路,特别强调了最后的向量法,并请每位学生掌握. 教师时间控制非常到位,讲解完后剩下5分钟时间进行课堂小结;学生活动的时间充分,在讲解过程中能体现新课程的一个特点——向量的工具性;能充分利用多媒体设备,特别是电子白板,使上课痕迹得到保存,便于学生课后查阅;但学生的活动还可以更完善(见感悟). 让学生先行,教师断后,构建有效课堂. 3.1 让学生充分发挥主体作用 新课程教学理念要求充分发挥学生的主体作用,做课堂的主人,这就要让学生多思多想、多做多练、多交流,同时也给教师的能力提出了更高的要求.笔者认为,要充分发挥学生的主体作用,可以从以下几个方面考虑: (1)例题要少而精,要有代表性.像课例中的一题多解课,一题足矣. (2)提倡先做后讲,让学生有充分的时间思考、动笔,让学生形成自己的思想、自己的思路,学会放手.如在此课例中,笔者通过让学生先做,然后让学生说、写,使学生进行充分的思考,但笔者在具体的处理上仍有赶的感觉,还没有做到真正放手,各种解法如果能让学生自己上来讲解,或者动用投影仪让学生上台讲解,效果可能会更好. (3)回归课本,充分体现数学思想.高考中很多问题都来自于课本,在最后的高考复习中,回归课本非常重要. 3.2 教师也要发挥主导作用 新课程要求充分体现学生的主体作用,同时也强调教师的主导作用,这就给教师提出了更高的要求.在这样的要求下,课堂变成了相对开放的课堂,可能会得到意想不到的结果,无论得到怎样的结果,都需要教师断后,做出理性的决定与思考.笔者认为,教师要发挥好主导作用,主要从以下几个方面来考虑: (1)对于学生出现的各种错误,教师要及时地进行纠正.比如课例中笔者通过巡视及时纠正了学生的个性错误,对于共性的错误,笔者在学生讲解后及时进行纠正,收到了良好的效果. (2)对于在自主探究以后学生得出的各种结论,教师要及时地用科学的语言加以总结、提炼.比如课例中的各种解法,学生能给出思路,但写法还不够完善,教师及时给出示范非常重要. (3)对于课堂小结,有些简单的可以让学生自己解决,但对于较抽象、专业的知识,由于学生能力有限,就需要教师进行科学的整理与正确的示范,这些过程必须由教师完成. 总之,在新课程教育理念下的课堂教学,已不再是简单的组织教学、讲授知识、巩固知识、运用知识和检查知识来展开,要强调合作学习、探究学习,要把所有学生的学习都提高到一个自主学习的高度.这就需要教师寻求更符合新课程理念的教学方式,构建有效课堂.笔者一直在思考和摸索,上面这个课例是笔者的初步尝试,主要目的是让学生在课堂上成为真正的主人,真正体现以学生为主体、教师为主导的理念,真正做到“自主、合作、创新”.前方的路还很艰辛,有待于我们共同探索与研究. [1] 缪荷芳.一节高三“一题多解”课的听课感悟[J].中学数学教学参考:上旬,2012(1/2):24-26.


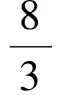






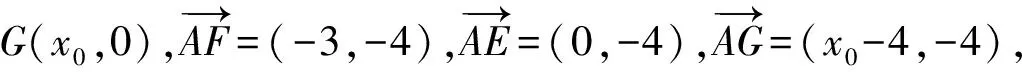

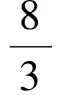


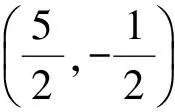


2 课例评说
3 感悟
