水轮机的振动特性研究

赵 燕 王丹萍

(1.浙江富春江水电设备股份有限公司，浙江 410013;2.上海勘测设计研究院，上海 200434)

随着经济发展对电力需求的不断提高，当今水电机组的水轮机尺寸和输出功率越来越大，虽然制造工艺和材料强度都得以提高，但在高转速和大的水头变幅条件下，无论是轴流式还是混流式，水轮机部件的刚度和运行的稳定性问题日益突出。但凡旋转部件，就不可避免的会产生振动，水轮机的转轮、导流叶片和旋叶等部件在自身转动惯性、重力、离心应力、水流的不稳定性冲击以及导叶尾缘脱体卡门涡的周期性扰动等因素的作用下，很容易失稳并诱发振动。即使不发生共振，水轮机若长期工作在高频的激振条件下，其部件也很容易发生疲劳损坏，如叶片发生裂纹等［1］。若激振频率与部件的水下共振频率一致时，将会导致水轮机部件的严重损坏，如导叶的断裂等。这不仅仅会影响机组水轮机本身的机械寿命，所引发的问题也会降低供电质量，高频振动的噪音也会严重恶化机组操控人员的工作环境。同时，机组的振动在很大程度上也会诱发水电厂房的振动并引发坝体高应力部位产生裂缝，造成重大的财产损失和安全隐患。历史曾多次出现导叶和旋叶的疲劳断裂事故，由此人们进行了大量细致的研究，并得出了许多阶段性的研究成果，如叶片、转轮在空气中的自振特性等［2］。

随仿真模拟技术和计算力学的发展，对水轮机部件的振动特性的研究也呈现出了新的特点。由过去的单一依靠实验测量，变为高质量、低成本的计算与实验的结合。由于水轮机转子叶片与水这种可认为不可压的工质直接接触，水流在流经导叶片后在叶片尾缘脱体，对转子部件造成高频的周期性的动载荷扰动。在假设直接与叶片接触的流体部分的各物理参数与柔性的叶片表面的物理参数相同的前提下，叶片的颤振又会直接影响流体的稳定性，之后流体的附加后的振动再进一步作用于叶片，也就是所谓的流固耦合问题。单一的求解流体或者固体部分的控制方程并未能得到理想的结果。在水轮机选型和设计阶段，对水轮机在水下的的各阶共振特性准确把握是工程建设的必要前提。本文基于有限元方法，建立并求解水轮机部件的流固耦合控制方程，研究水轮机在水下的振动特性。也就是将流体的简化后的N-S 方程和固体部分的结构动力方程耦合计算求解，并将水轮机部件在空气中和水中的振动特性做比较，以期对水电机组的建设提供参考［3、4］。

1 水轮机振动特性的数学模型

对于流固弹性问题而言，其结构的动力响应问题和载荷下变形以及稳定性问题都需要研究。对于水轮机而言，其固有频率与其在与流体相互作用时的频率是有所区别的。流固耦合(Fluid-Solid Interaction，FSI)是固体力学与流体力学相结合的一个学科分支，其涉及问题往往具有强烈的非稳态、非线性特性，计算区域中流体域和固体域共存，但不能单独求解且往往无法显式的消去用来描述流体域的独立变量和用来描述固体域的独立变量。该处理方法是计算数学、物理学和计算机科学的结合。在对物理模型进行合理的简化之后，建立相应的数学模型，对方程组进行迭代求解。在绝对坐标系下，描述不可压缩流体运动的张量形式的N-S 方程可简化为公式(1)所示形式，由于不涉及热量交换问题，因此描述流固耦合问题只需要流体部分的连续方程和动量方程［5］。

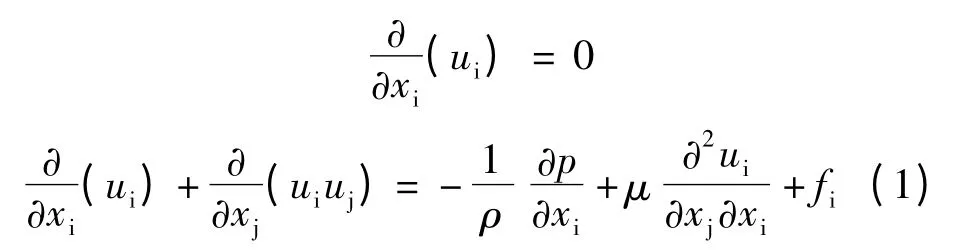
式中，下标i 和j 为张量表达式变量表示法，对于三维问题，其取值为1、2 和3，代表三个坐标方向，且i 和j 不同时取同一个值，并默认使用爱因斯坦求和约定;u 为速度;p 为压力;ρ 为密度;μ 为粘性系数;f 为体积力项。本文将采用双精度SIMPLE 算法，并用二阶迎风格式离散对流项，和标准K-e 湍流模型来求解流体域。

描述固体域部分的静力学有限元方程是

式中，K 为整体刚度矩阵;u 为各节点速率;Fs为流体的流动对流固交界面施加的压力;Ft为水轮机自身旋转而产生的惯性力。

当流场中的水流速度不为零时，最终的弹性场不仅与弹性固体边界的形变相关，流场入口的初始迭代值也会对结果产生重大影响，因为扰动水压产生附加质量的同时，对阻尼项和刚度项也会有直接的影响。若迭代求解方程组，判定迭代是否该结束或者是否收敛的标准是整个物理场的参数将不再明显的随迭代步数的递增而变化，就是物理场对跌代此处已不再敏感时即可结束迭代，比如当相邻两次的计算得到的某物理量之值相差小于0.2%时即可结束迭代［6］。

2 流固耦合计算

耦合计算的主要目的是获取相关部件在水中的自振特性，因此该算例的主要目的是给出处理问题的方法，并选用典型结构尺寸的转轮部件来分析该特性。本文以水轮机转轮为例，计算模型如图1 所示，其网格节点数量为10 万左右，转轮外部包裹的控制域即为流体域。

该结构在空气中的自由振动的控制方程是

式中，U 表示计算节点的位移向量;MS表征该结构的质量矩阵;Ks则表示刚度矩阵。流-固相互作用时其各自的自由振动控制方程是

图1 耦合后的计算域模型网格图Figure 1 Grid chart of calculation domain model at post-coupling

将公式(3)和公式(4)合并后可得到描述该耦合系统物理过程的完整的控制方程

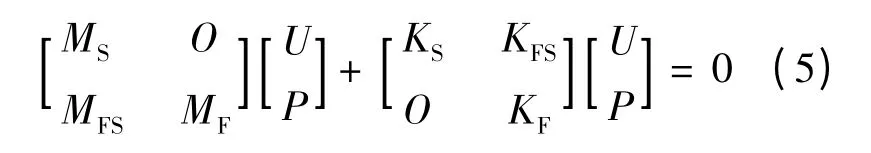
式中，MFS为耦合系统的质量矩阵;KFS为耦合系统的刚度矩阵。

计算给出了转轮在空气和水中的各阶固有频率，其中基本相等的两个相邻的两阶固有频率在本质上是同一阶振动在两个垂直方向上的具体表现。模拟对象在空气和水中的前7 阶各固有频率如表1 所示。

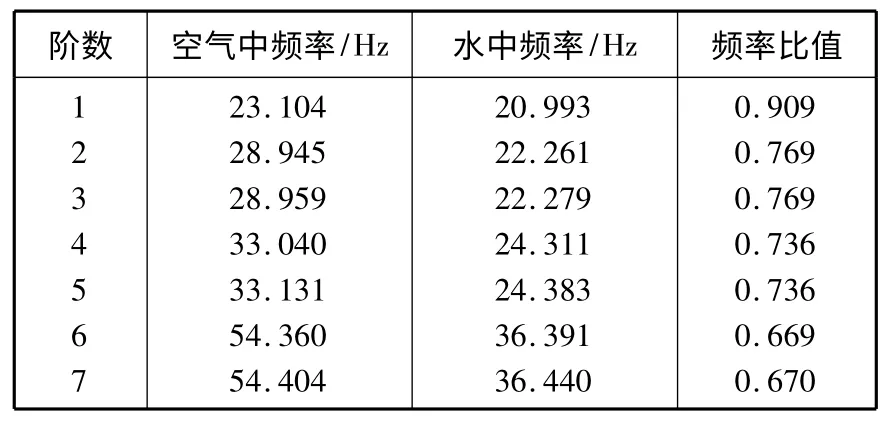
表1 前7 阶空气中和水中固有频率及比值Table 1 Natural frequencies of air and water ＆ ratios of the prior 7 steps

计算结果表明，转轮在水中的一阶固有频率与叶片的转动频率21.667 Hz 接近，是最有可能形成共振的频率。各运行工况下导叶尾缘脱体卡门涡列的频率范围为64 Hz～125 Hz，这与转轮自身的高阶固有频率可能重合并引发共振。与在空气中的转轮的固有频率不同，在水中时，转轮的固有频率会有所降低，但其降低程度是非线性的。与其他相关文献的计算结果对比表明，水流对转轮固有频率的影响机制随转轮几何结构的不同而不同，因此针对性的研究各结构在各工况下的振动特性十分必要。

3 改善振动特性的措施

现阶段，叶型的设计已经有相关数据库和分析软件，在进一步提高加工工艺和材料屈服强度的同时，一些用来改善水轮机振动特性的相关措施也是必不可少的。

(1)加设稳流装置。通过对水轮机周围流场的仔细分析和研究，例如通过数值计算得到具体的流场参数分布后，可有针对性的在流场内加设一些流阻不大但可有效限制流动脉动的设备装置。例如在转轮下设置十字架头，改变转轮导流锥流型等。相关的实践经验表明这些都是极为有效的防止共振发生的方法。

(2)补气。机组在部分负荷工况下运行时，在转轮下方会形成真空区，会导致叶片根部的水流形成漩涡，降低输出功率的水轮机效率。对该部位补气可有效解决这个问题。实验研究结果表明，在小负荷区域补气会由于气体均衡了流速场分布而导致流量和效率提高，特别是能均衡尾水管核心区的负值速度场，进而加大了转轮下侧面的压力，但当开度较大时，此处的分散的能量却得不到合理的利用。对于高转速和低水头工况的水轮机补气会导致机组出力特性变差。对于高转速机组补气则可能带来效率降低的不利影响。因此，在具体实施时要有针对性，具体问题具体分析。

(3)修整叶片出水边角度。修整叶片出水边角度可在高负荷工况下很大幅度的降低尾缘流体的脉动，进而降低引发水轮机共振的几率。且随最优化的运行特性向更大流量的推移，还可增加机组的效率，由此带来显著的经济效益。

4 结论

本文以三维有限元方法分析了混流式水轮机转轮的流固耦合振动特性问题。结果表明，水轮机的旋转部件在水中的振动特性与其在空气中单纯由转动引起的自振频率是不一样的，呈非线性下降趋势。且水轮机部件的疲劳裂纹的产生并不是由材料的静强度不够引起的，在接近共振的周期性动载荷的激励下，大应力部分产生高周疲劳是损坏的主要原因。随计算力学的发展，以相关流体力学商业软件如Fluent、CFX 等来模拟来求解流固耦合问题是水轮机振动特性研究的一个可能的发展方向。

［1］廖伟丽，逯鹏，梁武科，等.混流式水轮机转轮自振特性研究［J］.水力发电学报，2008(27):130－134.

［2］吕桂萍，唐任远.混流式转轮固有频率分析［J］.大电机技术，2006(1):53－55.

［3］党小建，梁武科，陈千文.水轮机刘谷耦合振动研究的发展趋势［J］.西北水力发电，2004(20):15－18.

［4］王泉龙.浅谈水轮机振动的研究［J］.大电机技术，2001(7):12－14.

［5］刘迎曦，李生，李守巨.基于遗传算法的水轮机振动参数识别［J］.计算力学学报，2003，5(20):541－545.

［6］马震岳，王溢波，董毓新.红石水电站机组振动及诱发厂坝振动分析［J］.水力发电，2000(9):52－60.