Logistic回归模型及其在对陶瓷坯体性能与组成之间关系建模中的应用*
2012-11-17高力明洪日辉李朝有刘蓓瑛
高力明 洪日辉 李朝有 刘蓓瑛
(1陕西科技大学 西安 710021)(2广西三环企业集团股份有限公司 广西 北流 537400)
Logistic回归模型及其在对陶瓷坯体性能与组成之间关系建模中的应用*
高力明1洪日辉2李朝有2刘蓓瑛2
(1陕西科技大学 西安 710021)(2广西三环企业集团股份有限公司 广西 北流 537400)
陶瓷坯体的性能的测定结果往往是以合格与否来表示的。对于这类只有2种取值的二分类定性变量,当以它们作为因变量去建立性能与组成之间关系的数学模型时,采用通常的最小二乘(OLS)回归方法存在许多问题。为此,我们引入了Logistic回归模型。笔者详细地介绍了Logistic回归模型,并给出了在陶瓷砖抗热震性建模中的成功应用示例,以供材料科学与工程领域的工作者参考与使用。
陶瓷 坯体性能 建模 Logistic回归模型
前言
材料工作者总是对材料的性能在某一组成区域中的分布及变化趋势感兴趣,并希望能借此找出满足预定材料的性能组成及适合的工艺条件。近年来,依照“回归的试验设计”的近、现代数理统计理论,并借助于计算机技术,人们在这方面的应用研究已经取得了很大进展[1]。并且已形成了一些程式化的,成熟的技术路线,且已得到推广使用,取得了良好的效果[2~3]。
关键的一步是建模。即利用试验的测试结果,对性能与组成之间的关系建立数学模型。建模一般可采用通常的最小二乘(OLS,Ordinary Least Square)回归方法。OLS回归方法简单规范,有良好的数理统计品质,其结果便于做工艺诠释,而且又有许多成熟的算法及软件可供调用。因此,OLS回归方法已得到广泛的应用,几乎成为标准的统计分析工具。但OLS回归方法的使用是有前提条件的,它通常要求因变量是间隔尺度(又称“测度”)变量,也就是平常所说的“连续变量”;它还要求自变量之间不能完全相关,这是OLS回归方法能够求解的条件。另外,它还有一些关于误差项的假设条件。因此,若将OLS回归方法用于有序(次序)尺度或名义尺度的因变量问题的求解,由于严重地违反了上述的基本假设和前提条件,将出现许多问题。诸如,会导致回归估计的推断存在严重的误差,以致无论是进行假设检验,或是计算置信区间,均使其失去合理性。也就是说,所得到的结果将是不可靠和不可信的,最终导致无法作出合理而有价值的工艺诠释。
在对一些陶瓷制品的性能进行测定与表征时,就有不少这种情况出现。例如,陶瓷砖的抗热震性、抗冻性,以及日用陶瓷制品的热稳定性等。依照相应的测定标准进行测试,得到的结果就只分“合格”与“不合格”2类[4~6]。当我们试图利用这些测试数据去建模时,就会遇到违反OLS回归方法的基本假设和前提条件的尴尬情况。这就需要寻找另外的解决途径与方法。
为此,我们拟引入Logistic回归模型及方法。该模型是基于Logistic函数(又称“增长曲线”),此函数形式是由比利时学者P·F·Verhulst于1838年提出的。经过多年的沉寂,直到20世纪20年代才在生物学研究中得到实际应用。之后,在人口估计和预测、经济学等多个领域中有了广泛的应用,重新受到世人的关注。我们也曾在企业营销活动的研究中有过应用[7]。借助于Logistic函数和概率论,将二分类的定性变量变换成Logistic曲线上的“连续变量”,从而使之又可以按照OLS回归方法对其进行处理,并对其结果作出合理的解释。这就是Logistic回归方法的思路和做法。
我们将对这种特殊的回归模型及方法做比较详尽的介绍,并且给出了在陶瓷砖抗热震性建模中的应用示例。从结果可以得出,Logistic回归方法对于二分类定性变量作为因变量时的建模是有效的、适用的。这一新的、特殊的回归模型及方法,进一步拓宽了多元统计分析在材料科学与工程领域中的应用范围,可供材料工作者在研究工作和开发新产品时参考与使用。
1 Logistic回归模型及方法
在配方问题中,为建立性能与组成之间关系的模型,所采用的广义线性回归方程的一般形式为:
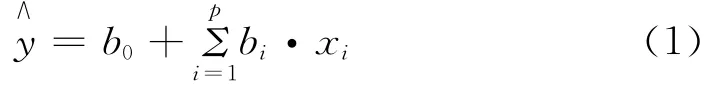
xi——自变量,一般为3大组成或元配料的各种成分数据及它们的高次项、交互项;
p ——自变量个数,即i=1,2,3,…,p;
b0,bi——分别为常数项及各自变量项的回归系数。
在材料科学与工程领域中,针对配方问题,因为有混料条件的约束限制,而更由于经常采用不完全多项式的广义线性形式,其试验方案多采用单纯形格子设计。
如前所述,对于性能测试值是间隔尺度的连续变量时,模型即式(1)的回归系数可以用OLS回归方法解出,并正常地进行各种检验和估计,但性能测试值若是二分类定性变量,就不能采用OLS回归方法。为此,我们需要引入新的模型及方法。Logistic回归的模型及方法可以较好地解决这一问题。
在Logistic回归模型中,首先要对因变量进行变换。定义一个新的因变量Z,并规定正变换为:

则很容易地推导出其反变换为:
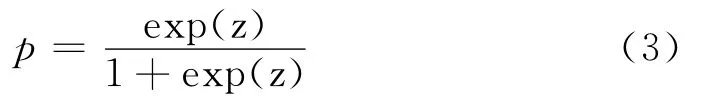
式(2)和式(3)中,p为原来的因变量得概率,0≤p≤1。
我们可以把性能的合格与否作为“事件”,并把p理解为事件“出现”的概率,那么(1-p)就是“不出现”(即“不合格”)的概率。比率p/(1-p)则是“发生比”。换句话说,新定义的因变量Z就是“发生比”的(自然)对数。此时,因变量Z已经变成一个连续变量。它与出现概率p之间的依存关系可以用表1和图1表示。由图1和表1可知,Z可以在(-∞,∞)之间任意取值,而且在进行反变换时,可以保证使p落在闭区间[0,1]之中,使其概率均有意义。

表1 Logistic函数的若干性状
如果仅用新的因变量Z取代原来的回归方程式(1)左部的因变量y,而自变量群,即右部维持不变,就变成Logistic回归模型。这时的回归方程已经满足OLS回归方法的基本假设和前提条件,因而可以采用OLS回归方法求解新的模型中的回归系数,并给出Z的估计值。然后,我们利用反变换式(3),就可以反算出“出现概率”p的估计值,并进行统计检验。
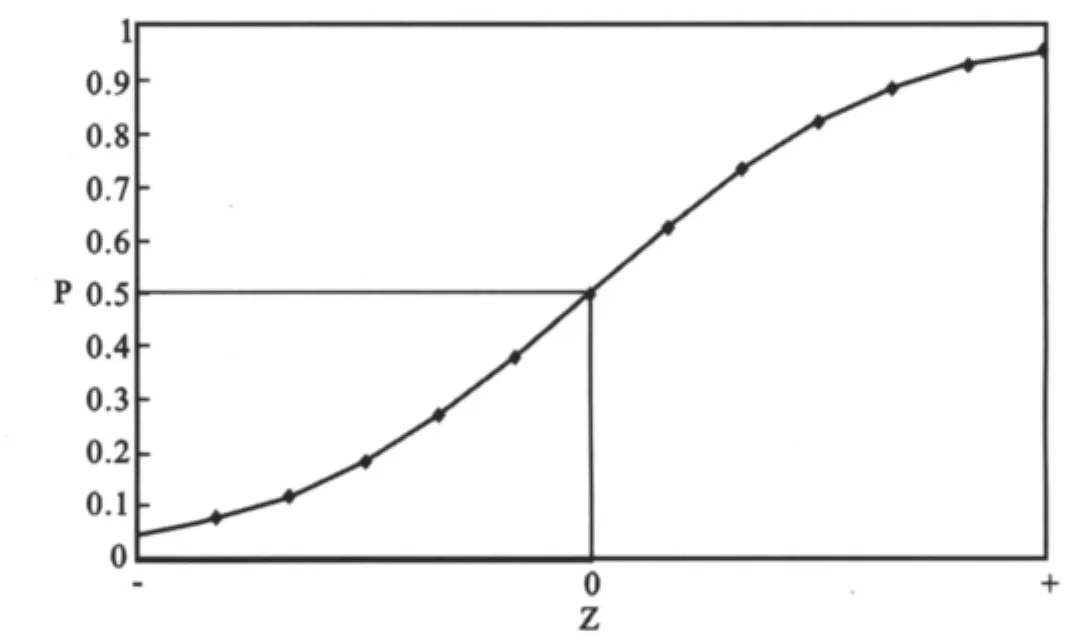
图1 发生比的对数Z与概率p之间的关系曲线
要指出的是,通常对得到的回归方程的显著性检验、复相关系数和F统计检验的解释与判断等,在这种情况下都是没有意义的。一种简便而有效的方法是采用“正确率C”(Correct rate)来检验,即通过回归模型对样本中的每一个样品的因变量进行评估,检查有多少个样品能够以此模型正确估计,然后以其占样品总数的百分比作为“正确率C”,进而对回归方程作出评价,判断是否能够通过检验,并加以应用[8]。
至于是否“正确”,则可以预先选定一个“阈值”,以此将因变量的预报值加以划分,并向两极“推移”,形成逻辑变量的“真”(True)与“假”(False),或者二分类定性变量的“合格”与“不合格”等。
在模糊数学中,认为隶属度在0.5附近时,事物是最模糊不清的。我们也常以0.5作为阈值,即认为>0.5是“真”(True),≤0.5是“假”(False)。
按照这样的约定,在实际操作时,就可以将Z的估计值为负的或为零的归为一类,即“不合格”;而将Z的估计值为正的归为另一类,即“合格”。从而重新形成二分类定性变量,以供分析和讨论。
2 Logistic回归模型示例
我们以一种陶瓷砖的抗热震性的测试结果作为示例,来演示利用Logistic回归模型建立该性能与组成之间关系的数模的过程。
试验是在预先选定的3种元配料为顶点的单纯形中,按3因子5分段的单纯形格子设计方案{3,5}给出的21个试验点上进行的。回归方程的右部是广义线性形式。实际采用的是自动满足混料约束条件的3次不完全多项式[9~10]。按照相应的国家标准测定了21组不同组成(原料配合比)试样的抗热震性,测试结果见表2。
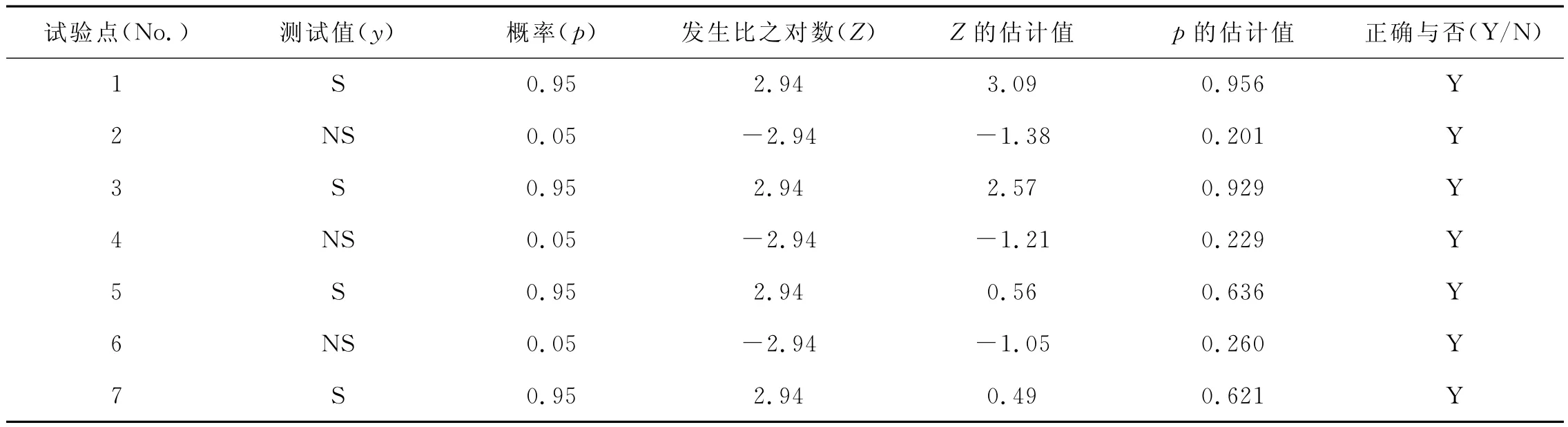
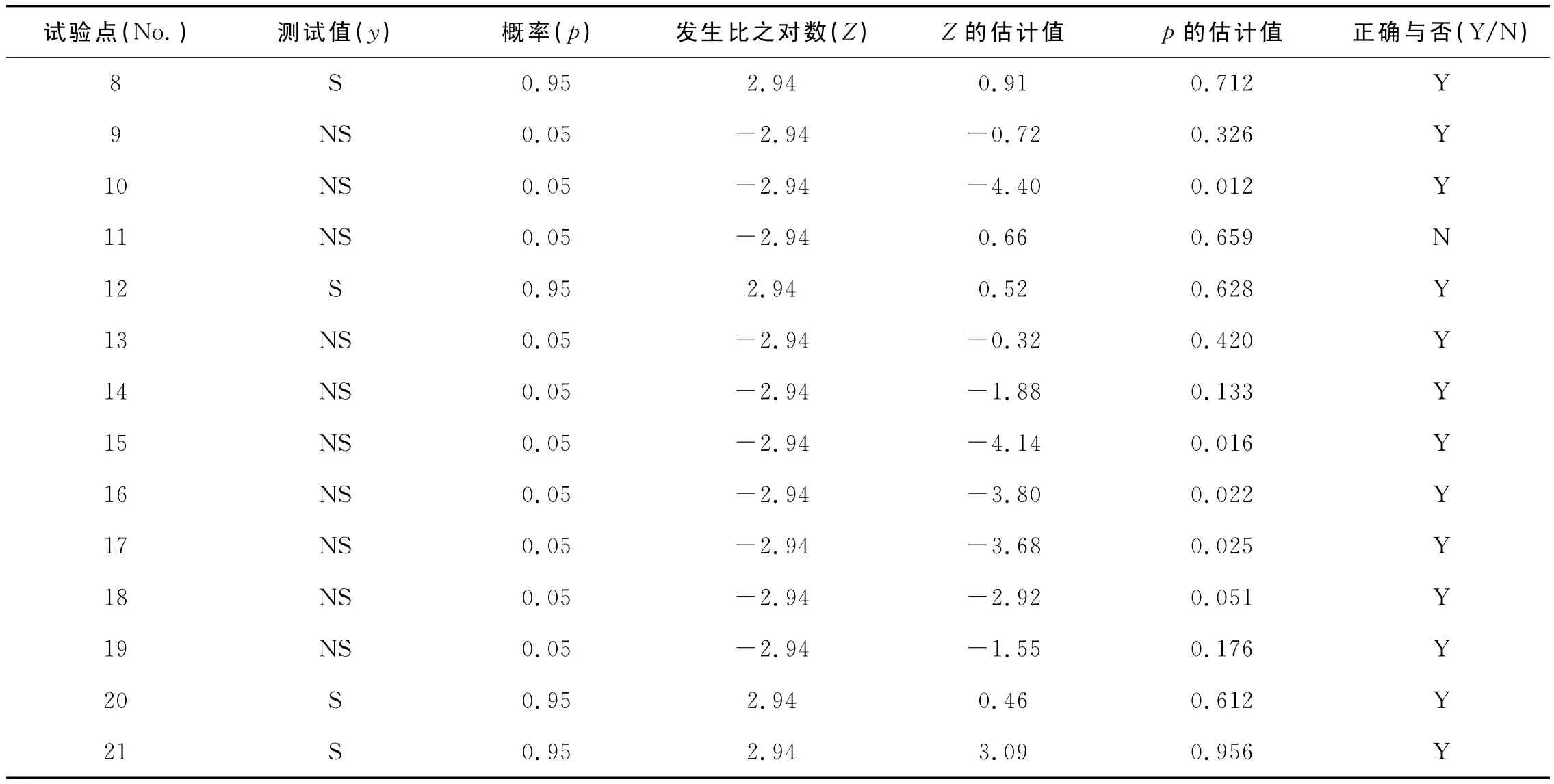
表2 陶瓷砖抗热震性测试值和建模结果
续表1
对于这些二分类定性变量,我们采用Logistic回归模型来建立性能与组成之间关系的数模。取对应于“合格”的概率p为0.95,因而不合格之概率即应取作(1-p)=0.05。再按式(2)进行正变换,对应于“合格”的Z值为2.94,而对应于“不合格”的Z值为 -2.94。代入式(1)的回归方程,用OLS回归方法求解,可得到一组回归系数b0和bi,以及Z的估计值。最后,再按式(3)进行反变换,即可得到概率p的估计值。
如果选定“阈值”为0.5,接下来就可以检视利用数模得到的估计值,在“二分类”意义下是否正确。结果显示在21个试验点中,对其中20个点的预报和估计是正确的,只有第11点的不符合。故正确率比较高,这说明利用Logistic回归模型是成功的。

3 结语
在陶瓷制品的性能测试中,有一些是采用二分类定性变量来表征的。要想建立这些性能与组成之间关系的数学模型,采用OLS回归方法是不可取的。这就需要一种新的回归模型。笔者介绍的Logistic回归模型及方法,是其中良好的一种。经过试用,证明在其材料科学与工程领域中同样适用,有较好的使用效果,并希望在使用过程中不断地改进与完善。
1 上海师范大学数学系.回归分析及其试验设计.上海:上海高教出版社,1978
2 高力明.材料成分及其制备工艺条件的CAD.陶瓷导刊,1992(3):25~28
3 高力明.元配料在材料性能之建模寻优方面的应用.全国性建材科技核心期刊——陶瓷,2005(9):8~11,15
4 GB/T 3810.9-2006,陶瓷砖试验方法 第9部分:抗热震性的测定
5 GB/T 3810.12-2006,陶瓷砖试验方法 第12部分:抗冻性的测定
6 GB/T 3298-91,日用陶瓷器热稳定性测定方法
7 高力明.我国陶瓷窑炉产业及其市场的形成与发展.中国陶瓷,2004(增刊):7~9
8 郭志刚.社会统计分析方法-SPSS软件应用.北京:中国人民大学出版社,1999
9 高力明.元配料之概念.陶瓷学报,2003,24(1):25~30
10 朱伟勇,等.最优化设计理论与应用.沈阳:辽宁人民出版社,1981
TQ174.75 文献表示码:A
1002-2872(2012)08-0020-03
高力明(1941-),教授;研究方向为陶瓷窑炉热工及计算机在材料科学领域的应用。
