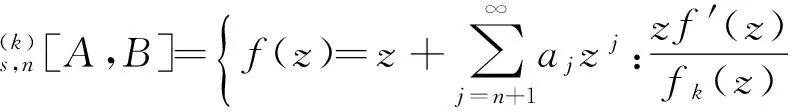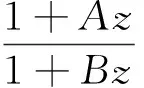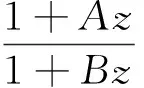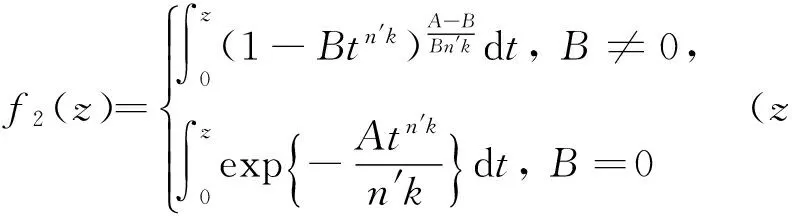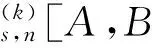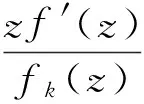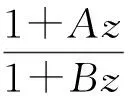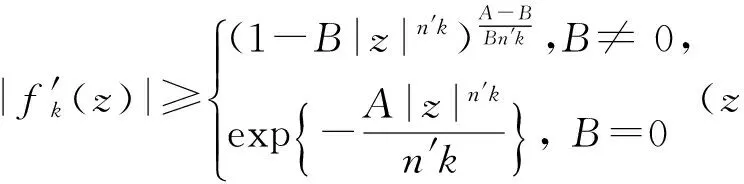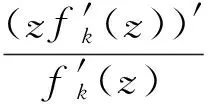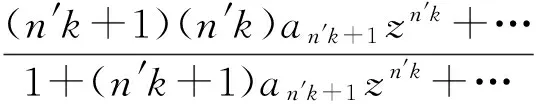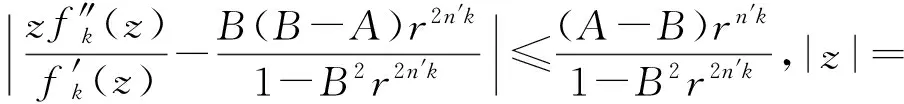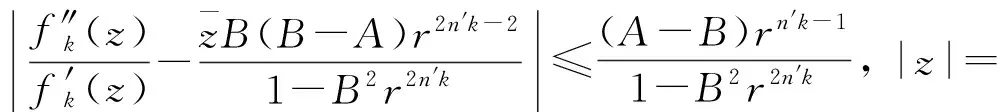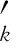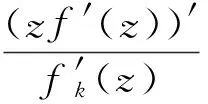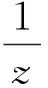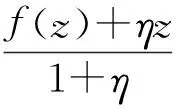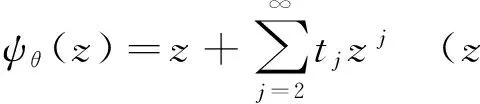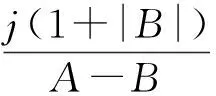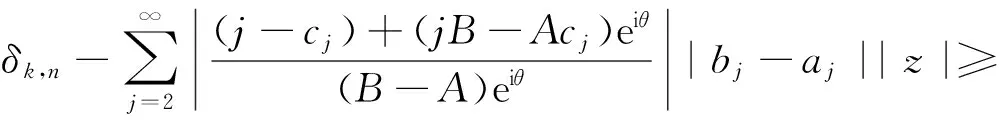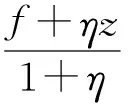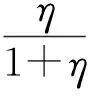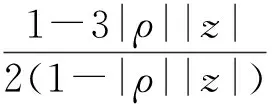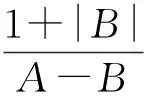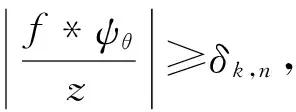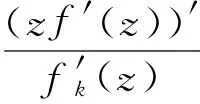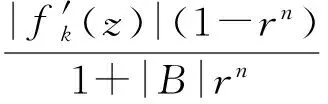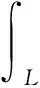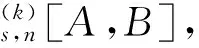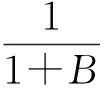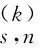关于k-折对称点的近于凸函数和拟凸函数子类的邻域
2012-11-14刘名生黄蕥媛
刘名生,黄蕥媛
(华南师范大学数学科学学院,广东广州 510631)
关于k-折对称点的近于凸函数和拟凸函数子类的邻域
刘名生*,黄蕥媛
(华南师范大学数学科学学院,广东广州 510631)
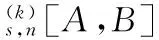
单叶函数; 近于凸函数; 拟凸函数; Hadamard 乘积;k-折对称点;δ-邻域
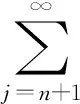

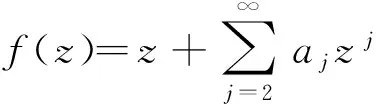
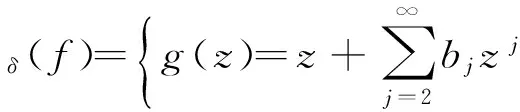


假定k,n≥1 是2个取定的正整数,-1≤B 和 其中fg表示函数f从属于g,fk(z)由下式定义: (ε= exp (2i/k),εk=1), 这里 (1) 根据引理 1, 可得 注意到g(0)=G(0)=0,和 所以 对z=r证明我们的估计是充分的,否则可以考虑fk的一个旋转. 此时有 (2) 如果B≠0,在式(2)两边积分, 可得 引理4 假定 -1≤B (3) (4) 根据ψθ的定义和Hadamard乘积的性质可得 (5) (6) 其中ψθ(z)由式(3)定义. (7) δk,n(1-|z|)>0. (8) 直接计算可得 注2 在定理 1和推论1中令k=1 和n=1, 可得文献[2]的相应结果. 对于B≤0,δk,n的值是最好的可能. 根据定理 1 的证明, 有 于是可得 现在根据ψθ的定义或者式(5),应用最小值原理可得 根据引理 3, 可得 (9) 取定 0 根据引理 4知,f*ψθ是单叶的,所以从0到(f*ψθ)(z0)的线段的原像L是 |z|≤r内的一条弧. 从而可得,对于 |z|≤r,有 |(f*ψθ)(z)|≥|(f*ψθ)(z0)|= 由式(9)可得 令 和 (0 显然有v′(r)<0 (0 (10) 这样式(11)的右边确定δk,n. 为了证明δk,n是最好的可能, 可考虑 [1] RUSCHEWEYH S T. Neighbourhoods of univalent functions[J].Proc Amer Math Soc,1981,8:598-601. [2] SHEIL-SMALL T,SILVIA E M. Neighbourhoods of analytic functions[J].J Anal Math,1989,52:210-240. [3] RAVICHANDRAN V. Starlike and convex functions with respect to conjugate points[J].Acta Math Acad Paedagog Nyhazi(N.S.),2004,20:31-37. [4] WANG Zhigang,GAO Chunyi,YUAN Shaomou. On certain subclasses of close-to-convex and quasi-convex functions with respect to k-symmetric points[J].J Math Anal Appl,2006,322:97-106. [5] 刘志文, 刘名生. 某类解析函数子类的性质与特征 [J].华南师范大学学报:自然科学版,2010(3):11-14. [6] FOURNIER R. A note on neighbourhoods of univalent functions[J].Proc Amer Math Soc,1983,87:117-120. [7] RUSCHEWEYH S T,SHEIL-SMALL T. Hadamard products of Schicht function and the Pólya-Schoenberg conjecture[J].Comment Math Helv,1973,48:119-135. [8] BROWN Johnny-E. Some sharp neighbourhoods of univalent functions[J].Tran Amer Math Soc,1985,287:475-482. [9] FOURNIER R. On neighbourhoods of univalent convex functions[J].Rocky Mtn J Math,1986,16:579-589. Keywords: univalent function; close-to-convex function; quasi-convex function; Hadamard product;k-symmetric points;δ-neighborhood OntheNeighborhoodsofCertainSubclassesofClose-to-ConvexandQuasi-ConvexFunctionswithRespecttok-SymmetricPoints LIU Mingsheng*, HUANG Yayuan (School of Mathematics, South China Normal University, Guangzhou 510631, China) 2011-02-21 教育部高等学校博士学科点专项科研基金项目(20050574002) *通讯作者,liumsh@scnu.edu.cn 1000-5463(2012)01-0014-05 O174.51 A 【责任编辑 庄晓琼】