一个混合型实齐次核的Hilbert 型积分不等式
2012-11-14谢子填
谢子填,曾 峥
(1.肇庆学院数学系,广东肇庆 526061; 2.韶关学院数学系,广东韶关 512005)
一个混合型实齐次核的Hilbert 型积分不等式
谢子填1*,曾 峥2
(1.肇庆学院数学系,广东肇庆 526061; 2.韶关学院数学系,广东韶关 512005)
应用权函数的方法,给出了一个新的混合型实齐次核的Hilbert 型积分不等式及其等价形式, 同时证明了常数因子的最佳性.
Hilbert型积分不等式; 权函数; Hölder不等式
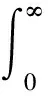
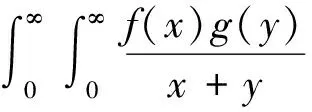
(1)
近年来包括积分型和级数型的Hilbert型不等式,人们陆续作了推广[2-9],这些基本上是负齐次核的.
2008年,文献[2]证明了如下核为-3齐次的具有最佳常数因子的Hilbert型积分不等式:

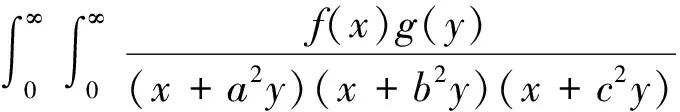
(2)
近年一些实数齐次的Hilbert型积分不等式陆续被发表,本文应用权函数的方法给出一个新的实数齐次核的Hilbert型积分不等式及其等价形式.


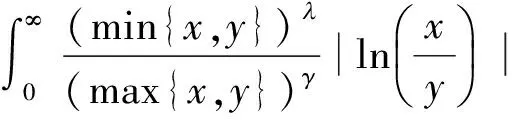
则有
(3)
证明设y=ux,则
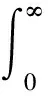
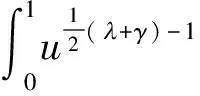
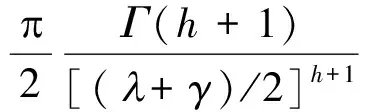
(4)
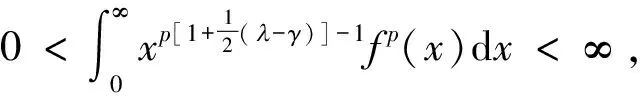
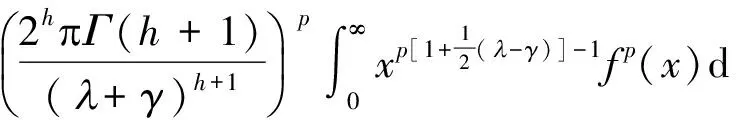
(5)
证明由带权Hölder不等式及式(3),有
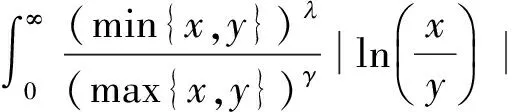
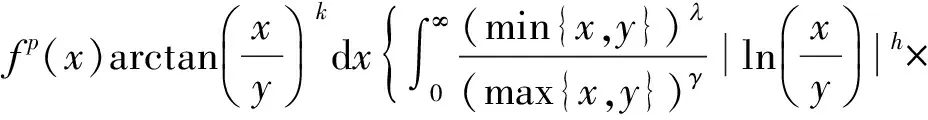
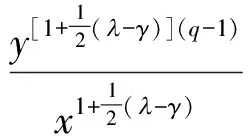
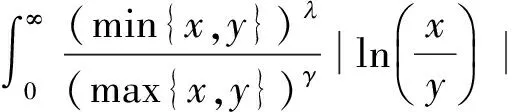
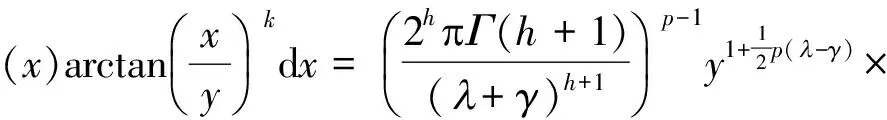
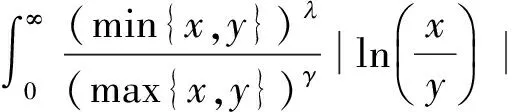
(6)
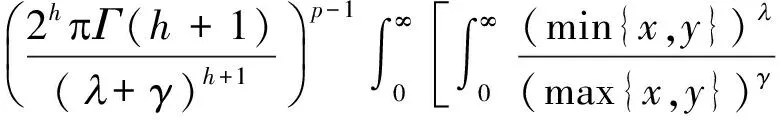
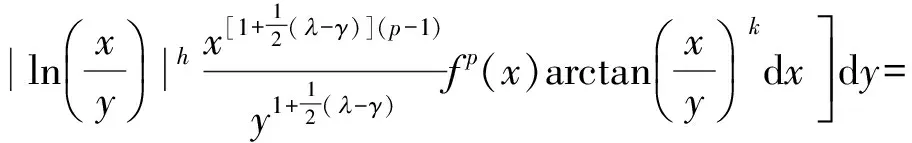
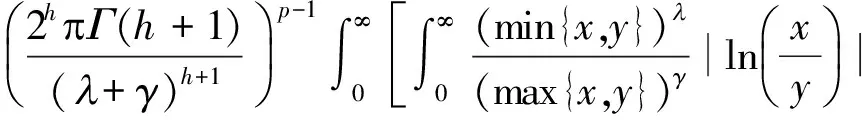
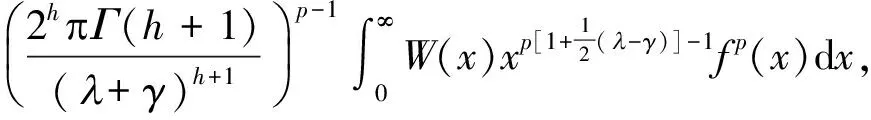
再由式(3)得式(5).
定理1 设p>1,f(x),g(x)≥0,
则有如下互相等价且均有最佳常数因子的不等式:
f(x)g(y)dxdy<
(7)
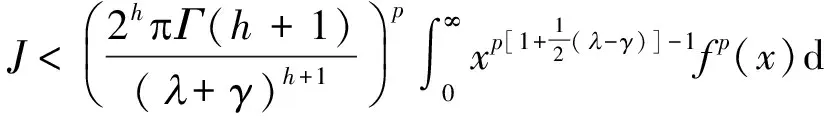
(8)
证明若式(6)对某个y>0取等号,则有不全为零的常数M和N(不妨设M≠0),使
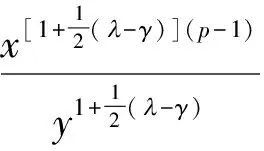
于(0,∞)几乎处处成立.故有常数C,使
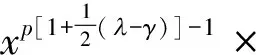
(9)
由式(8)得式(7),反之设式(7)成立.令
则
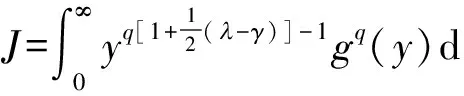
由引理1及条件知J<∞.若J=0,则式(8)自然成立;若0 故式(7)与式(8)等价. (10) (11) (12) (13) (14) 证明类似定理1的证明,由逆向Hölder不等式,容易知道式(13)成立.类似知式(12)成立,令g(y)如定理1,当然J>0.若J=∞,则式(13)成立;若0 上式两边除以J1/q,知式(13)成立,且与式(12)等价. (15) (16) (17) [1] HARDY G H. Note on a theorem of Hilbert concerning series of positive terems[J]. Proceedings London Math Soc,1925,23(2):XLV-XLVI. [2] XIE Zitian,ZHENG Zeng. A Hilbert-type integral inequality whose kernel is a homogeneous form of degree -3[J]. J Math Appl,2008(339):324-331. [3] 杨必成. 一个零齐次核的Hilbert型积分不等式及逆式[J].西南大学学报:自然科学版,2009,31(10):143-148. [4] 谢子填. 一个核为-3μ齐次的Hilbert型不等式[J].吉林大学学报:理学版,2007,45(3):369-373. [5] XIE Zitian. A reverse Hilbert-type inequality with a best constant factor[J].J Math Anal Appl,2008,343:1154-1160. [6] 谢子填.一个实数齐次核的Hilbert型积分不等式[J].吉首大学学报:自然科学版,2011,32(4):26-30. [7] 曾峥,谢子填.一个新的有最佳常数因子的 Hilbert型积分不等式[J].华南师范大学学报:自然科学版,2010(3):31-33. [8] 谢子填,曾峥.一个实齐次核的Hilbert 型积分不等式及其等价形式[J].浙江大学学报:理学版, 2011,38(3):266-270. [9] 谢子填,杨必成,曾峥.一个新的实齐次核的Hilbert 型积分不等式[J].吉林大学学报:理学版,2010,48(6):941-945. AHilbert-TypeIntegralInequalitywithaMixHomogeneousKernelofRealNumber-Degree XIE Zitian1*, ZENG Zheng2 By estimating the weight function, a new Hilbert-type integral inequality with a mix homogeneous kernel of real number degree is given in this work.The equivalent inequality and the reverse form are also considered. 2011-01-26 国家自然科学基金项目(10926128) *通讯作者,gdzqxzt@163.com 1000-5463(2012)03-0036-04 O178 A 10.6054/j.jscnun.2012.06.008 Keywords: Hilbert-type integral inequality; weight function; Hölder’s inequality 【责任编辑 庄晓琼】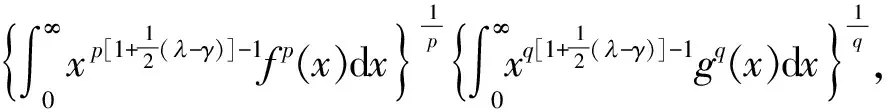
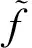
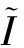
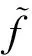
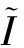
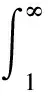
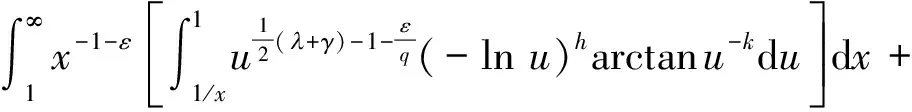
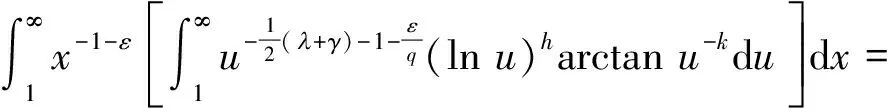
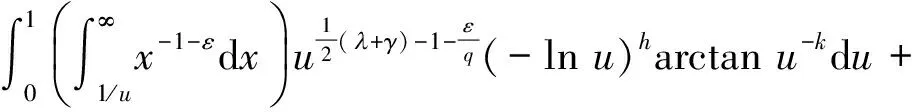
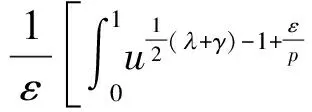
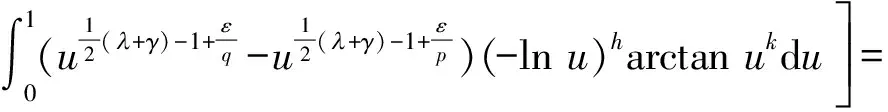
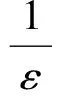
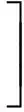
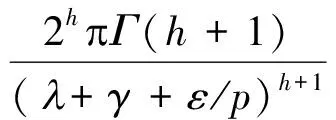
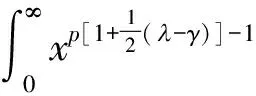
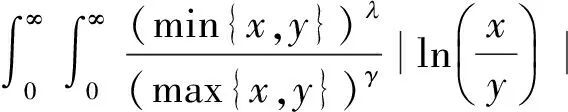
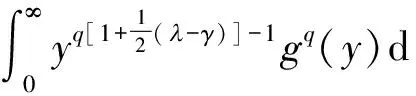


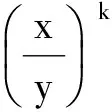

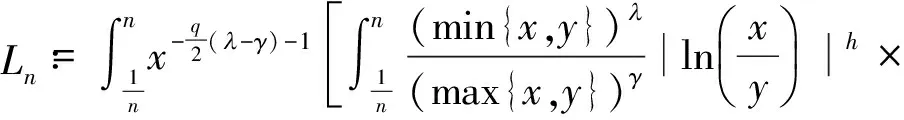
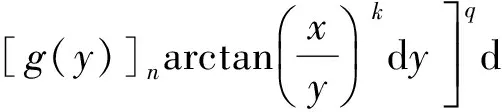

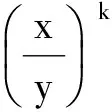
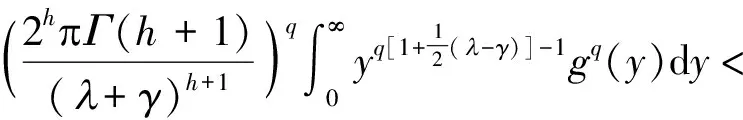
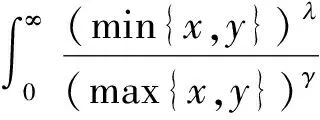
(1.Department of Mathematics, Zhaoqing University, Zhaoqing, Guangdong 526061, China; 2. Department of Mathematics, Shaoguan University, Shaoguan, Guangdong 512005,China)
