H(curl)-椭圆问题不连续Galerkin法的后验误差估计
2012-11-14邢小青钟柳强
邢小青, 钟柳强
(华南师范大学数学科学学院, 广东广州 510631)
H(curl)-椭圆问题不连续Galerkin法的后验误差估计
邢小青, 钟柳强*
(华南师范大学数学科学学院, 广东广州 510631)
针对Lipschitz多面体区域上H(curl)-椭圆问题的不连续Galerkin法, 提出了一种新的基于残量型的后验误差估计, 并证明了该后验误差的一个上界估计. 其中问题的最困难性在于如何处理跳跃项中出现的局部网格尺寸的负次幂.
不连续Galerkin法; 后验误差估计;H(curl)-椭圆问题
令Ω是三维欧氏空间3中的一个有界单连通Lipschitz多面体区域,∂Ω和n∂Ω分别是其连通边界和单位外法向量. 引入标准Sobolv空间H(curl;Ω)={v(L2(Ω))3n∂Ω×u=0 on ∂Ω}.


(1)
其中
a(u,v)=(×u,×v)+(u,v),
(·,·)表示函数空间L2(Ω)中的内积.
变分问题(1)可以应用于多种电磁场模型的数值模拟[1-2],不连续Galerkin (DG: Discontinuous Galerkin)法与其他有限元法相比较, 在某些方面更具有优势, 如保局部守恒性和稳定性方面等. 关于模型问题(1), 只有少量的研究文献是关于混合型内罚不连续Galerkin 法 (IPDG: Interior Penalty Discontinuous Galerkin)[3-4]. 据知, 关于DG法的后验误差估计的分析仅出现在文献[5]中. 但误差指示子太过于复杂, 以及依赖于一些计算区域的嵌入参数. 本文给出了一种新的基于残量型的后验误差估计, 与文献[5]的结果相比较, 误差估计更为简洁. 同时, 证明了后验误差的一个整体上界估计, 其中最困难的地方在于跳跃项中出现了局部网格尺寸的负次幂. 我们证明了该跳跃项可以被后验误差子所控制住.
本文第1节引入关于模型问题(1)的IPDG离散格式,第2节引入一种新的基于残量型的后验误差估计子及相关的预备知识;第3节给出了IPDG法后验误差的一种整体上界估计.
1 IPDG离散格式
(v,w)=vwdx,∀v,w(L2(Ω))3,
∀y,z(L2(h))3.
令H1(Ω;h)={vL2(T):vT=vT±, 则定义



引入通常的离散有限元空间


ah(uh,vh)=(g,vh), ∀vhVh,
(2)
其中
ah(w,v)=(×w,×v)+(w,v)-[[w]],
μ.
(3)
这里常数μ>0表示罚参数及hf表示面f的直径.
由文献[6]知,当罚参数满足μ≥μ0时, 离散变分问题(2)的解是存在唯一的, 其中常数μ0仅依赖于网格的形状正则及逼近阶数l.
2 后验误差估计子及预备知识








(4)
其中hT表示单元T的直径, 且有hT≈hf(即它们是相容的).在本文中, 除了特殊的常数外, 为了避免重复使用一般的常数记号,采用记号:,和≈,即当存在正常数C1,c2,c3和C3,满足x1≤C1y1,x2≥c2y2,c3x3≤y3≤C3x3成立时,则简记为x1C1y1,x2c2y2,x3≈y3.
定义

(5)
注1 与文献[5]的基于残量型的后验误差估计子相比较,式(5)中项数更少,表达形式更简洁.
下面引入提升算子Lh:(H1(Ω;h))3Vh满足
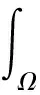
(6)
上述算子是稳定的[7],即
‖Lh(v)‖L2(Ω)‖‖L2(h),
(7)
其中上述常数仅依赖于网格的形状正则和有限元函数的多项式次数.
故可将由式(3)定义的双线性ah(·,·)改写为:
ah(w,v)=(×w,×v)+(w,v)-
(Lh(w),×v)-(Lh(v),×w)+
μ (8) ah(u,v)=(g,v),∀vH0(curl;Ω). (9) 关于IPDG法,当罚参数满足μ≥μ0时,如下性质成立(分别见文献[5]的引理4.1和文献[7]的式(15)): 有界性:ah(w,v)‖w‖h‖v‖h,w,vVh, (10) 强制性: ah(v,v)‖v‖h,vVh, (11) 其中依赖于网格的能量范数‖·‖h由下式给出 (12) (13) (14) ‖v-hv‖L2(T)+‖hf×(v-hv)‖L2(T) (15) 其中ΩT=∪f TΩf,Ωf={T′h,f⊂T′}. ‖v⊥‖hμ1/2‖‖. (16) 证明由式(11)和式(13)可知 则利用式(10)、(12)和[[wconf]]=0,有 ah(v-wconf,v-wconf)‖ 令wconf=hv,并利用式(15)即证得结论. 引理3[8]令V1,1(h)是第一类Nédélec线性有限元空间,则存在算子h)满足:对任意的vH0(curl;Ω),存在φ和z使得 hT‖φ‖0,T+‖φ‖0,T‖v‖0;ΩT, (17) 下面给出后验误差的第一个上界估计. ah(u-uh,u-uh)η2(uh,h)+‖[[uh]]‖. (18) ah(e,e)=ah(e,v-u⊥)= (19) (g,z+φ)-ah(uh,z+φ)= (R1(uh),z)-(R2(uh),φ)+J1(uh),z+ ‖hR1(uh)‖L2(h)‖h-1z‖L2(h)+ ‖hR2(uh)‖L2(h)‖h-1φ‖L2(h)+ ‖h1/2J1(uh)‖L2(h)‖h-1/2z‖L2(h)+ ‖h1/2J2(uh)‖L2(h)‖h-1/2φ‖L2(h)+ ‖Lh(uh)‖L2(h)‖×z‖L2(h) (η(uh,h)+‖[[uh]]‖L2(h))‖v‖h. 进一步,由v=e+u⊥和式(11),有 ‖v‖h≤‖e‖h+‖u⊥‖hah(e,e)1/2+‖u⊥‖h. 从而证得 (ah(e,e)1/2+‖u⊥‖h). 令C表示一个与参数μ无关的一般常数,则利用Young’s不等式和能量范数的定义(12),有 C(η2(uh,h)+‖[[uh]]). (20) 由Cauchy-Schwarz不等式、式(10)、(11)和Young’s不等式,可得 ah(e,u⊥)≤ah[(e,e)]1/2[ah(u⊥,u⊥)]1/2≤ 利用式(16)、(19)、(20)及上式,即证得结论. C1ah(uh,uh)=C1ah(uh-vconf,uh-vconf). (21) ah(uh-vconf,uh-vconf)= ah(uh,uh-vconf)-ah(vconf,uh-vconf)= (g,uh-vconf)-ah(vconf,uh-vconf). (22) 先估计上面第2项.利用式(8),Lh(vconf)=[[vconf]]=0,并改写vconf=uh+(vconf-uh),得 ah(vconf,uh-vconf)=(×uh,×(uh-vconf))- (vconf,uh-vconf)-(Lh(uh),×vconf). 利用分部积分公式及式(6),有 {{uh-vconf}}L2(oh)+(Lh(uh-vconf),×uh). 在上式中再次应用Lh(vconf)=0,可得到 ah(vconf,uh-vconf)=(×(×uh),uh-vconf)+ (Lh(uh),×(uh-vconf)). 把上式代入式(22)中,并利用式(4)和Cauchy-Schwarz不等式可知 ah(uh-vconf,uh-vconf)=(g,uh-vconf)- ah(vconf,uh-vconf)=(g-×(×uh)-uh, uh-vconf)-[[×uh]],{{uh-vconf}}L2(oh)+ vconf)-(Lh(uh),×(uh-vconf))≤ η(uh,h)(‖h-1(uh-vconf)‖L2(h)+ ‖h-1/2{{uh-vconf}}‖L2(oh))+ ‖Lh(uh)‖L2(h)‖×(uh-vconf)‖L2(h). 令vconf=huh并利用迹不等式、式(15)和式(7),有 ah(uh-vconf,uh-vconf)≤C2(η(uh,h)× 把上式代入式(21),有 作为引理4和引理5的一个直接结论,并利用式(11),得到如下关于误差的一个整体上界估计: [1] BOSSAVIT A. Computational electromagnetism: Variational formulation, complementarity, edge elments[M].San Diego, CA:Academic Press, 1998. [2] HIPTMAIR R. Multigrid method for Maxwell’s equations [J]. SIAM Journal on Numerical Analysis, 1999, 36(1):204-225. [3] CARSTENSEN C, HOPPE R. Unified framework for an a posteriori error analysis of non-standard finite element approximations ofH(curl)-elliptic problems[C]//IEEE International Conference on Electromagnetics in Advanced Applications(ICEAA’09). Torino, Italy, 2009: 754-755. [4] CARSTENSEN C, HOPPE R, SHARMA N, et al. Adaptive hybridized interior penalty discontinuous Galerkin methods forH(curl)-elliptic problems [J]. Numerical Mathematics: Theory, Methods and Applications, 2011, 4(1):13-37. [5] HOUSTON P, PERUGIA I, SCHOTZAU D. An a posteriori error indicator for discontinuous Galerkin discretizations ofH(curl)-elliptic partial differential equations [J]. IMA J Numer Anal, 2007, 27(1):122-150. [6] HOUSTON P, PERUGIA I,SCHENEEBELI A, et al. Interior penalty method for the indefinite time-harmonic Maxwell equations [J]. Numerische Mathematik, 2005, 100(3):485-518. [7] PERUGIA I, SCHOTZAU D, MONK P. Stabilized interior penalty methods for the time-harmonic Maxwell equations [J]. Computer Methods in Applied Mechanics and Engineering, 2002,191(41-42):4675-4697. [8] SCHOBERL J. A posteriori error estimates for Maxwell equations [J]. Mathematics of Computation, 2008, 77(262):633-649. APosterioriErrorEstimateofDiscontinuousGalerkinMethodforH(curl)-EllipticProblems XING Xiaoqing, ZHONG Liuqiang* A new posteriori error estimate based on residual for discontinuous Galerkin discretizations ofH(curl)-elliptic problems on Lipschitz polyhedron is proposed. The corresponding upper bound is proved. One of the most difficult problem here is how to deal with the presence of the negative power of the local mesh size in the jump term. 2012-02-25 国家自然科学基金项目(10971074; 11171359) *通讯作者,zhong@scnu.edu.cn 1000-5463(2012)03-0018-04 O241 A 10.6054/j.jscnun.2012.06.003 Keywords: discontinuous Galerkin method; a posteriori error estimate;H(curl)-elliptic problem 【责任编辑 庄晓琼】
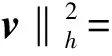
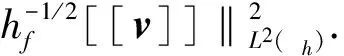

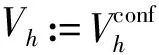



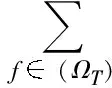



3 整体上界估计
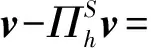

hT‖z‖0,T+‖z‖0,T‖×v‖0;ΩT.

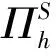
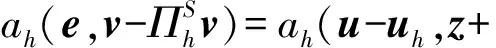
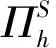

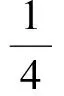


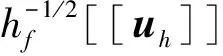

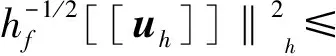



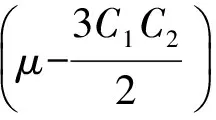

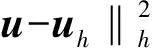
(School of Mathematics, South China Normal University, Guangzhou 510631, China)
