关于Rayleigh商矩阵近似特征值估计
2012-11-14董李娜
董李娜, 王 嫣
(1.河南教育学院数学系,河南郑州 450046;2.中州大学信息工程学院,河南郑州 450044)
关于Rayleigh商矩阵近似特征值估计
董李娜1*, 王 嫣2
(1.河南教育学院数学系,河南郑州 450046;2.中州大学信息工程学院,河南郑州 450044)
借助于谱分解定理以及矩阵理论中的特征值的排序、优于等相关性质定理研究Hermite矩阵近似特征向量与相应的Rayleigh商矩阵作为近似特征值之间的关系,进行特征值的扰动分析,并推广了一个应用广泛的结论.
Hermite矩阵; Rayleigh商矩阵; 近似特征值; 近似特征向量
Rayleigh商在计算特征值和特征向量中有着重要的应用[1-2],在利用计算机计算各类问题时,由于计算精度所引起的舍入误差、实验室设备在测量数据时所引起的观测误差、输入数据引起的误差等会影响计算解的准确性,导致通常矩阵的特征值难以直接求出.由于误差的存在,Rayleigh商是Hermite矩阵A的近似特征值,人们希望知道作为ρ(x)近似特征值的精确度,本文讨论了这个问题.文中使用符号规定:用Cm×n表示所有m×n复矩阵的集(m≥n);CN=Cn×1;Ik表示k阶单位矩阵;‖·‖表示谱范数;A*表示矩阵A的共轭转置.


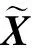
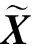
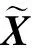


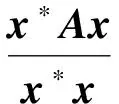
文献[2]、[3]曾研究过ρ(A)作为A的近似特征值的精确度与x作为A的近似特征向量的精确度的关系.
定理1[4]设x1是n阶Hermite矩阵A属于特征值1的特征向量.如果xCn,满足sinθ(R(x),R(x1))=Ο(ε),则ρ(x)-1=Ο(ε2).
文献[5]考虑上述问题的反问题,得到
定理2[5]设矩阵A的特征值为1≥2≥…≥n,对应的特征向量为u1,u2,…,un,令Uk=(u1,u2,…,uk),kCn×k,*kk=Ik.如果trace(k)≥1+2+…+k+ε2,那么
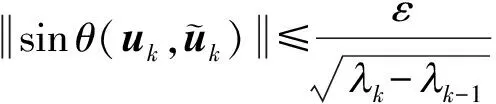
文献[6]中利用Rayleigh商研究了任意矩阵的奇异值.

易知,当A为Hermite半正定矩阵时,该定理就是定理1的推广.
下面例子说明定理1能推广到Hermite矩阵.
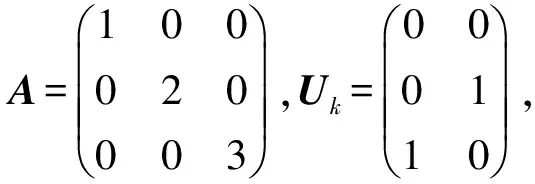
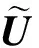
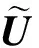
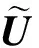
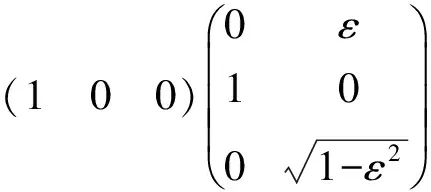
将定理1推广到更一般的情况,要用到下面的一些引理.

设A和的特征值分别用{i}和表示.且假定它们按递减顺序排列,即
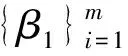


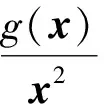
下面给出主要结论与证明,它推广了定理1.

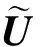

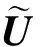
(1)
Y*Y+Z*Z=Ik.
(2)
设V*AV的谱分解为
V*AV=QΩQ*,
(3)

令Λk=diag(1,2,…,k),由AUk=UkΛk和式(1)得
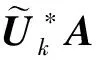
Y*ΛkY+Z*QΩQ*Z,
设Ik-YY*的特征值分解为
Ik-YY*=PΣP*,Σk=diag(σ1,σ2,…,σk),
其中σ1≥σ2≥…≥σk≥0.
trace(Λk)-trace(Y*ΛkY)=
trace(Λk)-trace(YY*Λk)=
trace((Ik-YY*)Λk)=trace(PΣP*Λk)=
trace(ΣP*ΛkP).
类似可得,
trace(Z*QΩQ*Z)=trace(Q*ZZ*QΩ).
由σ1≥σ2≥…≥σk≥0,diag(P*ΛkP)(P*ΛkP)=(Λk),以及引理2可得
trace(ΣP*ΛkP)≤σ11+σ22+…+σkk,
trace(ΣP*ΛkP)≥σ1k+σ2k-1+…+σk1.
同理得
trace(Q*ZZ*QΩ)≤σ1μ1+σ2μ2+…+σlμl,
trace(Q*ZZ*QΩ)≥σ1μl+σ2μl-1+…+σlμ1.
分情况讨论:
①当k≤l时,有
trace((Ik-YY*)ΛK)-trace(Q*ZZ*QΩ)≥
σ1k+σ2k-1+…+σk1-(σ1μ1+σ2μ2+…+σkμk)=
σ1(k-μ1)+σ2(k-1-μ2)+…+σk(1-μk)≥0,
trace((Ik-YY*)Λk)-trace(Q*ZZ*QΩ)≤
σ11+σ22+…+σkk-(σ1μl+σ2μl-1+…+
σkμl+1-k)=σ1[(1+2+…+k)-
(μl+μl-1+…+μl+1-k)]=m1σ1,
(4)
其中m1=(1+2+…+k)-(μl+μl-1+…+μl+1-k)≥0.
②当k>l时,有
σ1k+σ2k-1+…+σk1-(σ1μ1+σ2μ2+…+σlμl)=
σ1(k-μ1)+σ2(k-1-μ2)+…+
σl(k+1-l-μl)+σl+1k-l+…+σk1≥
-σ1(|k-l|+…+|1|)=-m2σ1,
其中m2=|k-l|+…+|1|≥0.
σ11+σ22+…+σkk-(σ1μl+σ2μl-1+…+σlμ1)=
σ1(1-μl)+σ2(2-μl-1)+…+
σl(l-μl)+σl+1l+1+…+σkk≤
σ1[(1+2+…+l)-(μl+μl-1+…+μ1)+
(5)
其中m3=(1+2+…+l)-(μl+μl-1+…+μ1)+|l+1|+…+|k|≥0.
由①和②可得
min{0,-m2}σ1=-m2σ1,
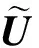
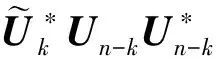
‖I-YY*‖=σ1,
其中U=(UkUn-k)为酉阵.由定理1的条件知σ1=O(ε2),再由式(4)和式(5)得
-m2σ1≤1+2+…+k-trace(k)≤
max{m1,m3}σ1,
所以有
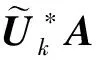
注1 定理4中取k=1时, 则有
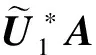
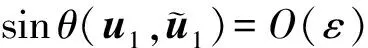
致谢:衷心感谢黎稳教授的悉心指导!
[1] HORN R A, JOHNSON C R. Topics in matrix analysis[M]. New York: Cambridge University Press, 1991.
[2] YANG X, SARKAR T K, ARVAS E A. Survey of conjugate gradient algorithms for solution of extreme eigenproblems of a symmetric matrix[J]. IEEE Transactions on Acoustics, 1989,37:1550-1555.
[3] STEWARD G W, SUN J G. Matrix perturbation theory[M]. Boston: Academic Press,1990.
[4] 孙继广.矩阵扰动分析[M]. 北京:科学出版社,2001.
[5] LI R C. Accuracy of computed eigenvectors via optimizing a Rayleigh quotient[J]. BIT, 2004, 44 :585-593.
[6] CHEN X S, LI W. On the Rayleigh quotient for singular values[J]. JCM, 2007, 5(25): 512-521.
[7] LI W, CHEN X S. The eigenvalue perturbation bound for arbitrary matrices[J]. JCM, 2006, 24: 141-148.
ApproximateEigenvaluesoftheRayleighQuotientMatrix
DONG Lina1*, WANG Yan
(1.Department of Mathematics, Henan Institute of Education, Zhengzhou 450046, China; 2.College of Information Engineering, Zhongzhou University, Zhengzhou 450044, China)
The relation between approximate eigenvalues and approximate eigenspaces for the Rayleigh quotient matrix of Hermitian matrices is considered. By using some related properties and theorems in matrix theory to analyze the perturbation of the eigenvalues, a widely used theorem existing in the literature is generalized.
2011-10-18
河南省科技攻关项目(112102310377);河南教育学院青年科研课题(20080104)
*通讯作者,dln3515@163.com
1000-5463(2012)03-0022-03
O241.6
A
10.6054/j.jscnun.2012.06.004
Keywords: Hermitian matrix; Rayleigh quotient matrix; approximate eigenvalue; approximate eigenvector
【责任编辑 庄晓琼】
