厚壁钢管压力矫直时的截面扁化计算

马更生，田雅琴，黄庆学

(太原科技大学，山西 太原 030024)

0 前言

截面扁化变形是钢管压力矫直加工过程中经常出现的问题，严重影响钢管的加工质量，建立精确的截面扁化数学模型能有效的指导工程实践，实现高效加工，对提高成材率有重要的现实意义。近年来，薄壁钢管截面扁化问题研究的报道比较多，但对厚壁钢管截面扁化问题的研究还很少见报道。本文根据弹塑性原理，对钢管中间加压截面处进行分析，得到了厚壁钢管在压力矫直过程中截面扁化的数学模型，以期认识厚壁钢管弯曲扁化的变形机理。

1 建立截面扁化模型

1.1 截面的轴向弯矩

压力矫直过程中，截面扁化最易发生在压头接触钢管的中间截面处，该处是整个钢管扁化变形中的最大变形处。

管材矫直时，塑性变形要深入到管内径，本文假设矫直过程中钢管的塑性变形已深入到管内径，设压力矫直的压下力为F，压点与支座的距离为l，钢管内径为r，外径为R，弹性极限层距中性层高度为 Rt，其中 Rt/R=ξ1，r/R=a，由内应力计算此时的压下力为

其中，Mt1为以R为半径的粗棒弹性极限弯矩，，σs为屈服应力。

1.2 截面的环向弯矩

由于中间截面的轴向弯矩Mz引起环向弯矩，而环向弯矩的存在是引起截面的扁化变形的主要因素。如图1中，ρ为钢管的弯曲曲率，α为(环向变形角)从x轴正向逆时针方向的角度。

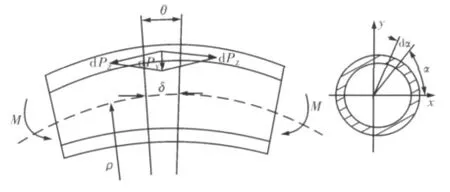
图1 钢管受力简图Fig.1 Diagram of steel pipe force distribution

取截面微元分析，在M的作用下，微元受到dPz为

其中，z为到中性层的厚度。

对钢管中截取角度为θ，厚度为δ的圆环的上部进行分析，截取部分如图2所示，可认为是简支曲梁，竖直方向作用有分布载荷的曲梁模型。

图2 曲梁受力简图Fig.2 Diagram of curved beam force distribution

1.3 截面扁化率

曲梁受到的等效载荷为

2 有限元模拟过程

2.1 建立模型

根据压力矫直问题的实际情况，通过大型通用有限元分析软件ANSYS/LS-NYNA进行分析，单元为3Dsolid164，材料为45号钢，模型简化为理想弹塑性材料，不考虑硬化特性，弹性模量为E=210 GPa，泊松比P为0.3，屈服极限σs=355 MPa。为简化计算，压头和支座定义为刚体模型，单元为3 Dsolid164，弹性模量为E=210 GPa，泊松比P为0.3。支座为全约束，压头只有Y方向可运动，接触面静摩擦系数为0.2，动摩擦系数为0.3，压下时间为10 s，保压时间为5 s，卸载时间为5 s。在ANSYS中建立模型，网格单元全部采用六面体单元，如图 3 所示［4］。

图3 钢管有限元模型Fig.3 Finite element model of steelpipe

2.2 有限元结果分析举例

图4～图6列出了外径是200 mm，厚径比为0.2的钢管矫直时情况，图4为压头施加到钢管的压下力曲线，在弹性阶段，压下力随时间线性变化，在保压阶段压下力不再增大，此时塑性变形已经深入到钢管内径，图5是钢管的中间截面的切片经过了矫直过程，中间截面扁化云图。图6是压头接触截面压点和支点位移曲线图，与图4对应，压头下行位移与压下力变化曲线相对应。节点A38359取自中间截面的压点，节点B40661取自曲梁支点，两者之间的位移差值即为变形挠度。

3 计算与仿真结果对比及分析

有限元仿真与理论公式计算的结果趋势一致，根据有限元仿真将理论计算公式修正为Ψ=f(0.1F－6.75)。表1和表2列出了理论计算与有限元分析的截面扁化对比数据。

考虑到厚径比太小时，钢管发生屈曲失效，厚经比过大时，钢管截面扁化现象不明显，本文给出厚径比为0.25和0.2的两种情况，图7和图8分别是厚径比为0.25和0.2的45号钢管在压力矫直的情况下，压下力与扁化率的关系，其中实线表示的是用截面扁化表达式计算的结果，虚线表示的是通过有限元程序模拟的结果，并且把相同厚径比的钢管压下力－扁化率曲线画在一起，以便进行计算和仿真数据的对比。截面扁化模型和有限元模拟的数据虽然存在一定的误差，但整体趋势是一致的，有限元总体误差范围小于32.5%，从图中可以看出，随着压下力增大，绝对误差增大，主要是由于截面扁化模型推导过程中，进行了模型理性化，没有考虑钢管中得剪切应力和摩擦力。

表1 厚径比为0.2时截面扁化模型与有限元模型计算结果Table 1

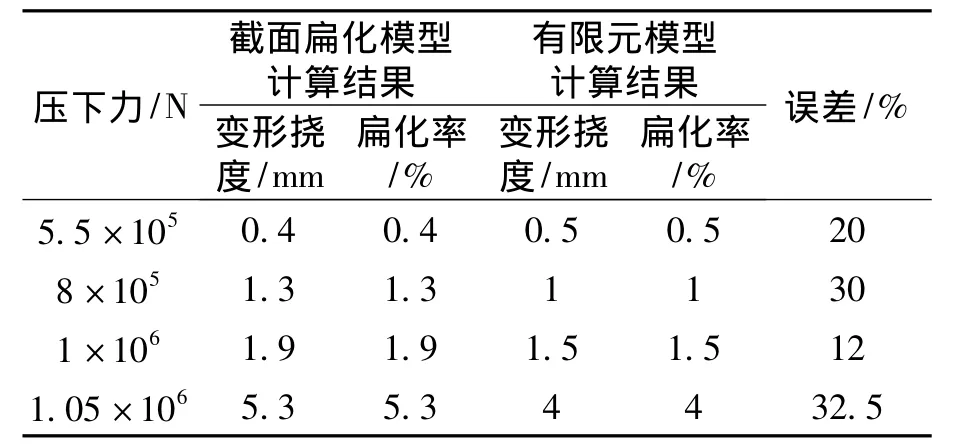
表2 厚径比为0.25时截面扁化模型与有限元模型计算结果Table 2

图7 厚径比为0.2的压下力-扁化率曲线图Fig.7 Pressure versus planation as thickness to diameter ratio is 0.2

图8 厚径比为0.25的压下力-扁化率曲线Fig.8 Pressure versus planation as thickness to diameter ratio is 0.25

4 小结

依据弹塑性理论，针对压力矫直过程中厚壁钢管截面扁化问题进行了分析，建立了厚壁钢管截面扁化数学模型，通过有限元软件对钢管压扁理论模型进行验证，截面扁化模型和有限元模拟的数据虽然存在一定的误差，但整体趋势是一致的，有限元总体误差范围小于32.5%。理论模型存在一定的局限性，其适用条件是材料为理想弹塑性材料。

［1］ 崔甫．矫直原理与矫直机械［M］．北京:冶金工业出版社，2002．

［2］ 李骏．基于校直过程模型的校直工艺理论及实验研究［D］．上海:上海交通大学，2005．

［3］ 王志飞，田雅琴，黄庆学等．基于LS-DYNA压力矫直钢管反弯挠度的计算［J］．重型机械，2010，(6):62－64，68．

［4］ 艾治勇．弯管的弯曲成形分析及其力学特性研究［D］．上海:上海交通大学，2005．