基于经验模态分解的大型轮船锚机齿轮箱故障诊断

张国华 郝刘仓 曹振芳

邯郸净化设备研究所，河北 邯郸 056027

1 引 言

作为一种传动装备，锚机齿轮箱庞大的体型和其拆装困难是其长期以来不易维修的重要原因之一。受工况条件所限，传统的信号处理技术，如FFT等［1］的故障诊断效果并不理想，这是因为信号中包括了船体、动力源、齿轮、轴承、齿轮箱本体以及锚机间的干扰等诸多因素。因此，在有限条件下采用何种方法对大型机械装备进行信号处理和故障诊断是亟待解决的问题。

用于齿轮与轴承上的信号处理与故障诊断的方法很多。其中，频谱分析［2］是一种整体变换，分析的结果为信号在频域内的统计平均值，不能反映信号的局部信息，因而其只能分析频率不随时间变化的线性和平稳信号。短时傅立叶分析［3-4］是在信号傅立叶变换前加上有限时间窗函数，通过窗在时间轴上的移动而使信号逐段被分析，从而得到信号的一组“局部”频谱。虽然该方法可用于时域局部化分析，但窗口没有自适应性，不适用于旋转机械中常见的多尺度信号和突变过程。Wigner-Ville分布［5］具有很高的时频分辨率，时频聚集性较好，且具有对称性、时移性、频移性和可逆性等特点，但其对多分量信号会产生交叉项，不宜分析复杂信号。小波分析［6-7］是一种时域与频域相结合的分析方法，具有良好的局部化特性，并可根据不同的需要选择不同的小波基函数和分解尺度，对旋转机械故障诊断具有很好的适应性，但是小波基函数和分解尺度的选定仍然缺乏系统性理论的指导，对于齿轮箱这样的复杂信号，若选择不当，就很难明确故障特征，因此需要具备丰富的故障诊断实践经验。另外，文献［8］还对小波基函数和分解尺度的选定进行了系统研究，并针对小波分析方法的某些缺点与局限性作了适当改进，最终运用改进的小波分析方法较准确地分析了F-15B／836战斗机变速箱的故障。文献［9］提出了磨损碎片与振动信号综合分析方法，即通过对不同故障状态的齿轮进行实验与分析，总结出一套较完整的诊断方法。

本文将以某大型轮船锚机齿轮箱为例，针对锚机齿轮箱振动信号的特性，拟采用经验模态分解法（EMD）对故障振动信号进行处理与分析。

2 经验模态分解法

EMD法［10-12］是基于信号的局部特征时间尺度，其通过对信号进行平稳化处理，并将信号中不同尺度的波动或趋势逐级分解，从而产生一系列具有不同特征尺度的数据序列，即固有模态函数（IMF）。其中，IMF满足如下条件：

1）整个数据段内极值点的个数与零交叉点的个数相等或相差不超过1个；

2）任何一点由局部极大值点形成的包络线和由局部极小值点形成的包络线的平均值为0。

假设原始信号为x（t），IMF的提取方法如下：

1）确定信号局部极值点，然后用三次样条曲线将局部极大值点和极小值点连接起来形成上、下包络线，并使上下包络线包络所有数据点。

2）上下包络线的平均值记为m1，得出：

若h1为1个IMF，则h1就是x（t）的第1个分量。

3）如果h1不满足IMF条件，便将h1作为原始数据，重复步骤1）和步骤2），得到上下包络线的平均值m11后，再判断h11＝h1-m11是否满足IMF的条件，如仍不满足，则循环k次，直至h1（k-1）-m1k＝h1k，使得 h1k满足 IMF 的条件。 记 c1＝h1k，则c1为信号x（t）的第1个满足IMF条件的分量。

4）将 c1从 x（t）中分离出来，得到：

将r1作为原始数据重复以上过程，得到x（t）的第2个满足IMF条件的分量c2，重复循环n次，得到信号x（t）的n个满足IMF条件的分量。故有：

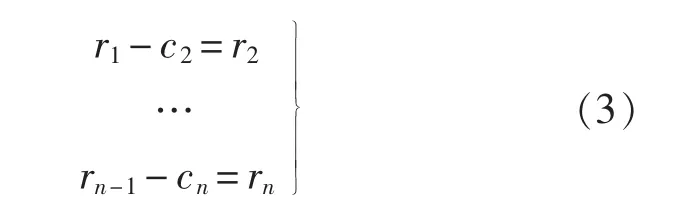
最后，当rn成为单调函数不能再从中提取满足IMF条件的分量时，循环便结束。

由式（2）和式（3）可得：

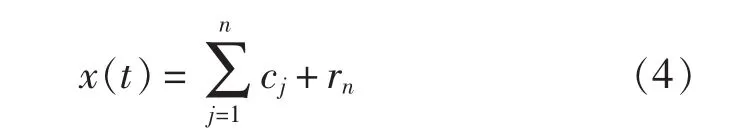
因此，可将任意一个信号x（t）分解为n个固有模态函数和1个残量rn之和。其中，分量c1，c2…cn分别包含了信号从高到低不同频率段的成分，并且每一频率段所包含的频率成分不同，是随信号 x（t）的变化而变化。 rn则表示了信号 x（t）的中心趋势。

锚机齿轮箱的内部传动参数如表1所示，内部结构如图1所示。

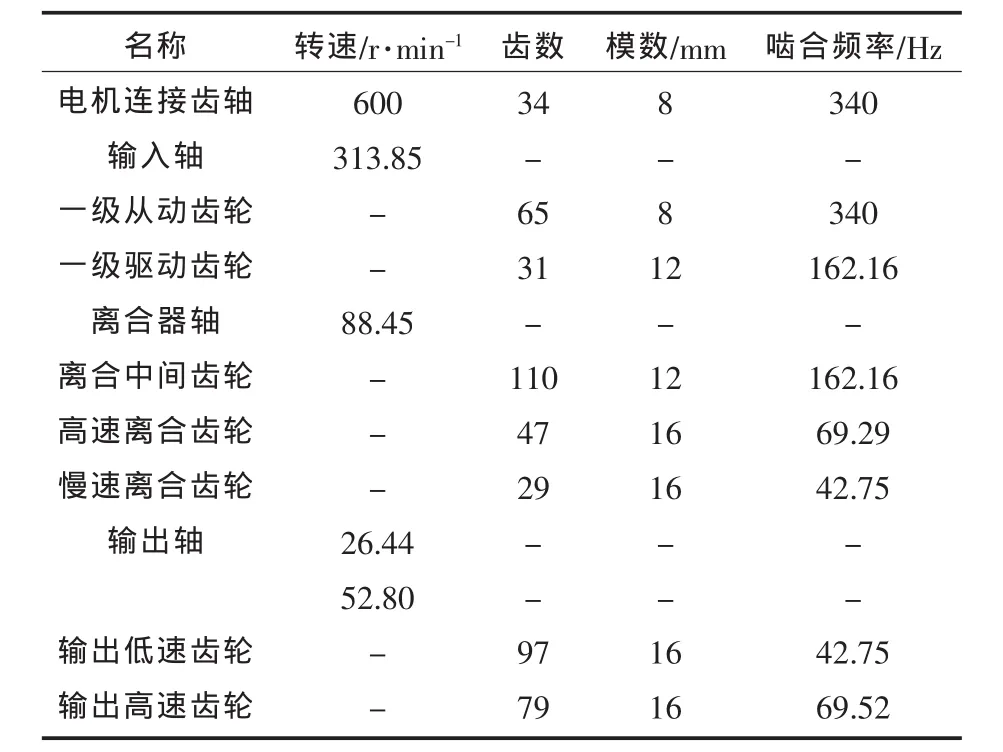
表1 锚机齿轮箱内部传动参数Tab.1 Transmission parameters of anchor gearbox

3 锚机齿轮箱故障诊断

3.1 数据的测量及预估

对锚机齿轮箱的振动信号进行采集时，首先使用B＆K4638加速度传感器和B＆K2635电荷放大器对信号进行获取与放大，然后用比利时LMS公司生产的LMS动态测试仪进行数据采集。其中，在采集过程中，采用5～1 000 Hz带通滤波器，Hanning窗函数。

将加速度传感器安装在4根轴的7个轴承座上，保持其与轴承外圆柱面垂直接触 （误差±0.5 mm）。用电缆线连接电荷放大器和传感器，并在接近振动区域处用树脂将其固定，以避免因轴承振动所引发的干扰信号而造成有用信号的扭曲。

给定锚机4个转速，即300 r/min、400 r/min、500 r/min和600 r/min，在各点采集振动信号并计算其均方根值，如图2所示。由图可见，在同一位置上，随着转速的提高，所测得的振动幅值增大，尤其是在最高转速下，电机连接齿轴对应轴承座上的振动幅值明显高于其他值。因此，初步断定该处结构可能出现了故障，或转速对应频率在共振点附近，后续的数据都由该点测得。

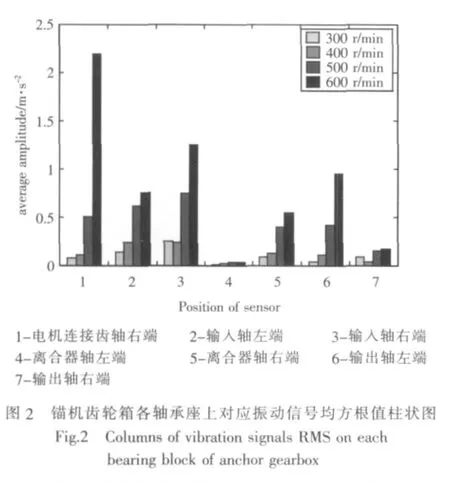
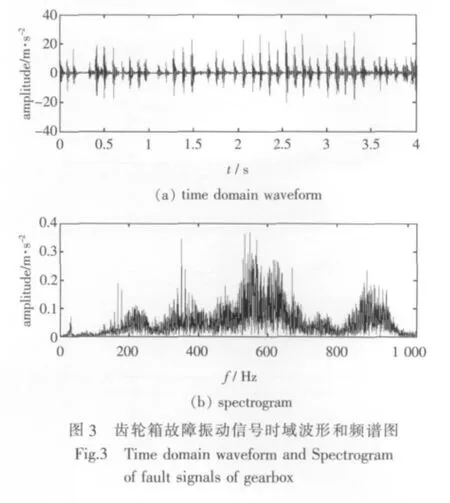
图3所示为通过位于轴承座测试点测得的电机连接齿轴处振动信号的时域信号及其频谱图。由图3（a）可看出存在明显的冲击现象。由图3（b）可看出，在频段175～250 Hz、350～400 Hz和50 0～600 Hz等处有幅值较高的谱峰出现，但是这些频率成分对应的振动来源不明，因此，要准确判断齿轮箱的故障还需做进一步的分析。

3.2 EMD分解与故障诊断

由以上频谱分析可看出，信号中有明显的冲击存在，但低频冲击的来源尚不明确。对上图测得的原始故障信号进行EMD分解，得到16个IMF分量，图4所示为振动信号EMD分解的IMF分量和各IMF分量的频谱图。本文只选取前8个IMF分量作为研究对象，并分别在其频域内提取特征指标。

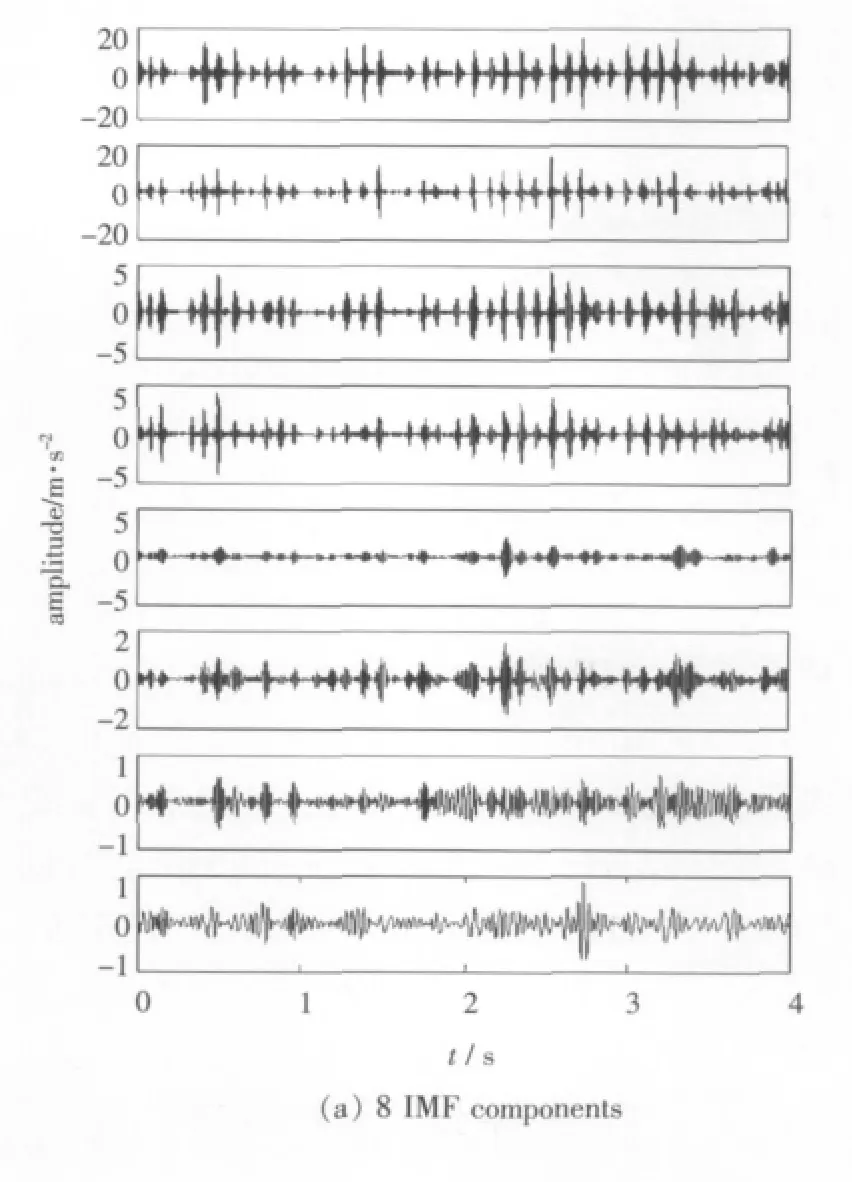
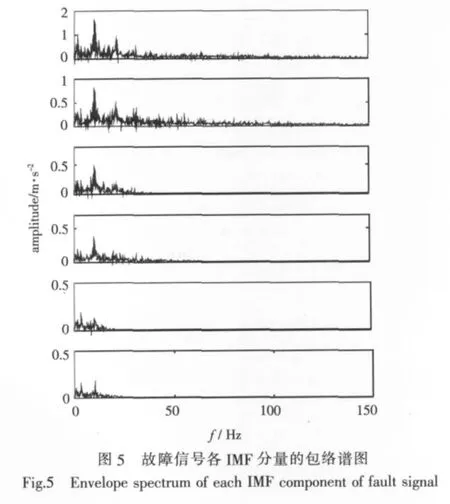
由图4可见，EMD将原始信号分解为若干个IMF分量，不同的IMF分量包含不同频段所对应的能量。但仅由此还难以分析出齿轮箱的故障所在。对各IMF分量分别作Hilbert变换，得到包络谱（图5）。由第1层IMF的包络谱图可以发现，在10 Hz处幅值最大，有明显的冲击现象，该频率与电机连接齿轮轴的转频吻合，并且在20 Hz处有0.7 倍的幅值，在 30 Hz处有 0.35 倍的幅值，由此说明，在转频的倍频处存在高次谐波。此外，从其他IMF分量也可得出相同的结论。由此可判断，齿轮箱发生强烈的振动是因电机连接齿轴旋转不平衡而导致。

4 诊断结果验证

将电机轴拆卸后，发现该轴的孔径为φ180.06 mm，超出了图纸要求的上限 φ180.04 mm，另外，圆孔的原始面上有补焊痕迹。由此说明，以上缺陷使得箱体轴承孔上的轴承外圈和箱体轴承孔在装配过程中存在问题，造成轴承在内孔中刷圈（图6），致使内孔产生带状沟而影响装配质量，最终导致电机连接齿轴旋转不平衡。

给定 4 个转速，即 300 r/min、400 r/min、500 r/min和600 r/min，在4根轴7个轴承座处分别采集振动信号，对应信号的均方根值柱状图如图7所示。

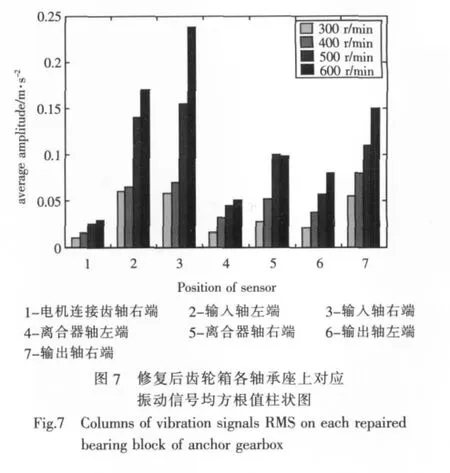
由图可见，各轴承座上信号的振动幅值差别不大，而且电机连接齿轴对应的幅值相比修复前已明显降低。

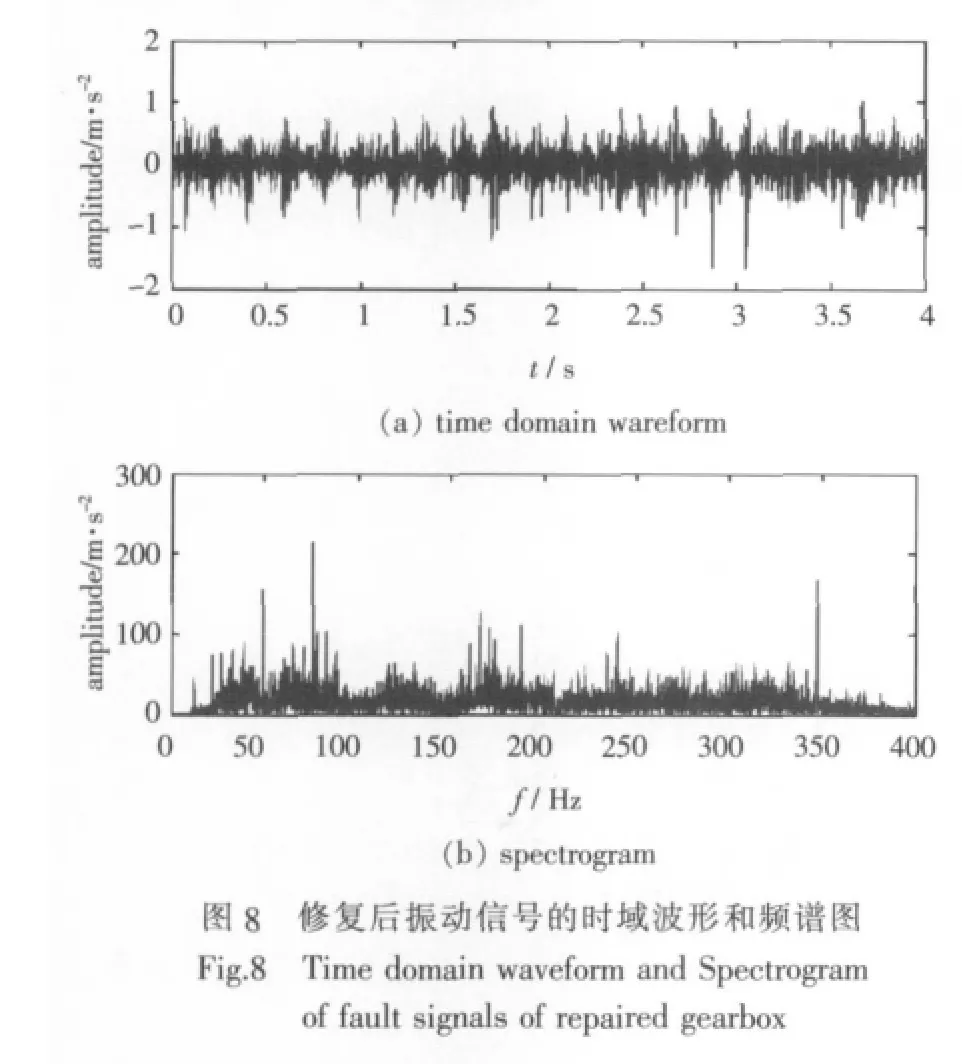
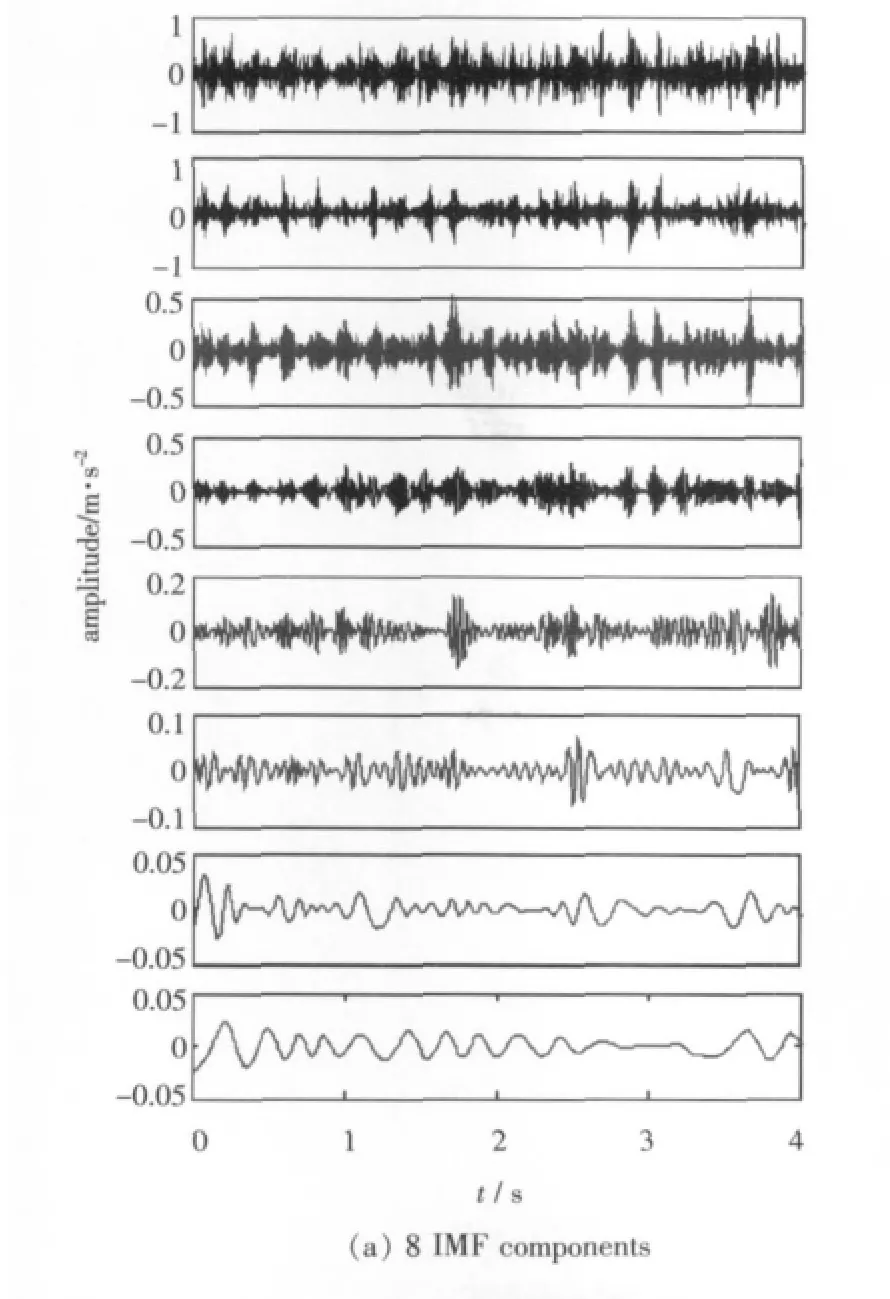
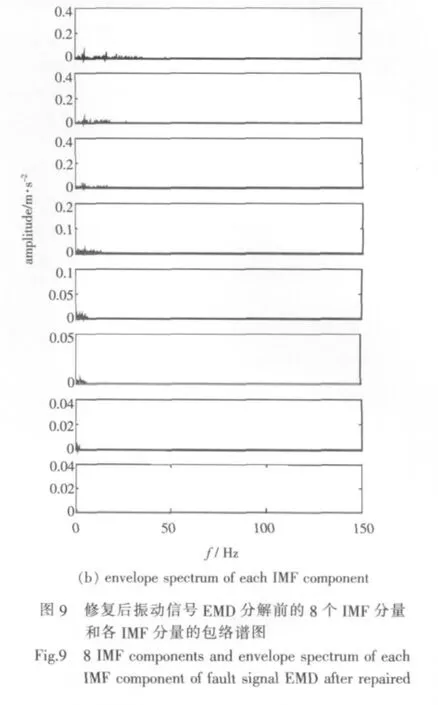
在电机连接齿轴右端所测信号的时域波形和频谱图如图8所示。对该信号进行EMD分解，所得各IMF分量及其包络谱如图9所示。由图可见，齿轮箱经修复后已不存在明显的冲击现象，并且信号幅值与故障存在时相比要小得多。

5 结 语

本文针对锚机齿轮箱故障的诊断系统与振动信号处理方法进行了研究，并将EMD方法应用到诊断过程中，其可准确、有效地提取故障特征信息。最后，对故障部位进行修复并再次采集信号进行处理与分析，结果表明，EMD法可以很好地解决大型锚机齿轮箱的故障诊断问题。

［1］HAYASHI I，IWATSUKI N，Universal FFT and its application［J］.International Journal of the Japan Society for Precision Engineering，1991，25（1）：70-75.

［2］BELSAK A，FLASKER J，Failure diagnostics of a gear unit［J］.Structures and Materials，2004，14（1）：255-264.

［3］SAFIZADEH M S，LAKIS A A，THOMAS M.Using shorttime Fourier transforms in machinery fault diagnosis［J］.International Journal of COMADEM，2000，3（1）：5-16.

［4］RANDALL R B，Applications of spectral kurtosis in machine diagnostics and prognostics［J］.Key Engineering Materials，2005，293（9）：21-32.

［5］STASZEWSKI W J，WORDEN K，TOMLINSON G R.Timefrequency analysis in gearbox fault detection using the Wigner-Ville distribution and pattern recognition［J］.Mechanical Systems and Signal Processing，1997，11 （5）：673-692.

［6］ZHOU X Y，YE Y Z.Application of wavelet analysis to fault diagnosis［J］.Control Engineering China，2006，13（1）：70-73.

［7］CHINMAYA K，MOHANTY A R.Monitoring gear vibrations through motor current signature analysis and wavelet transform［J］.Mechanical Systems and Signal Processing，2006，20（1）：158-187.

［8］CARY S，CAJETAN M A，HAMORY P.An approach to vibration analysis using wavelets in an application of aircraft health monitoring［J］.Mechanical Systems and Signal Processing，2007，21（4）：1255-1272.

［9］PENG Z，KESSISSOGLOU N.An integrated approach to fault diagnosis of machinery using wear debris and vibration analysis［J］.Wear，2003，255（10）：1221-1232.

［10］HUANG N E，SHEN Z，LONG S R，et al.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［C］//Proceeding of Royal Society，London，1998.

［11］HUANG N E，WU M L，LONG S R.A confidence limit for the empirical mode decomposition and the Hilbert spectral analysis［C］//Proceedings of the Royal Society，London，2003.

［12］于德介，程军圣，杨宇.机械故障诊断的Hilbert-Huang变换方法［M］.北京：科学出版社，2006.