捕捉高考共鸣点 把握高考新动向——高考整数题盘点
2012-11-06
●
(浬浦中学 浙江诸暨 311824)
捕捉高考共鸣点把握高考新动向——高考整数题盘点
●王苏文
(浬浦中学 浙江诸暨 311824)
很多省份都实行了高考独立命题,各省的高考试卷中常出现一些共鸣点,如2011年的高考卷中有几份试卷都出现了有关整数问题的试题.整数问题在高中数学竞赛中经常遇到,在高考试卷中出现较少.在这么多的省份中尤为突出的是陕西省和安徽省,陕西省已连续2年出现与整数有关的试题,安徽省同一份试卷出现了2道与整数有关的试题,着实让高考试题在横向、纵向上都形成了共鸣.根据这些高考整数题,笔者大致将其分为3类:整点类、方程类、条件类.
1 整点类
整点类问题在解析几何中是一种常见题型,如直角坐标系下的整数点、线性规划中符合条件的整数解等.整点具有特殊性,我们正好利用这个特殊性进行解答,如排除法.
例1设A(0,0),B(4,0),C(t+4,4),D(t,4)(t∈R).记N(t)为ABCD内部(不含边界)的整点的个数,其中整点是指横、纵坐标都是整数的点,则函数N(t)的值域为
( )
A.{9,10,11} B.{9,10,12}
C.{9,11,12} D.{10,11,12}
(2011年北京市数学高考理科试题)

例2在平面直角坐标系中,如果x与y都是整数,就称点(x,y)为整点,下列命题中正确的是____________(写出所有正确命题的编号).
①存在这样的直线,既不与坐标轴平行又不经过任何整点;
②如果k与b都是无理数,则直线y=kx+b不经过任何整点;
③直线l经过无穷多个整点,当且仅当l经过2个不同的整点;
④直线y=kx+b经过无穷多个整点的充分必要条件是k与b均为有理数;
⑤存在恰经过一个整点的直线.
(2011年安徽省数学高考理科试题)
分析考查直线方程,同时也考查了逻辑推理能力,难度较大.

y1-y2=k(x1-x2),
故点(x1-x2,y1-y2)也在直线y=kx上,即直线y=kx经过无穷多个整点.将y=kx上下平移得到y=kx+b,从而直线y=kx+b也经过无穷多个整点,故③正确.
因为k与b都是有理数,所以直线y=kx+b不一定经过整点,故④错误.

例3设实数x,y满足不等式组

若x,y为整数,则3x+4y的最小值是
( )
A.14 B.16 C.17 D.19
(2011年浙江省数学高考理科试题)
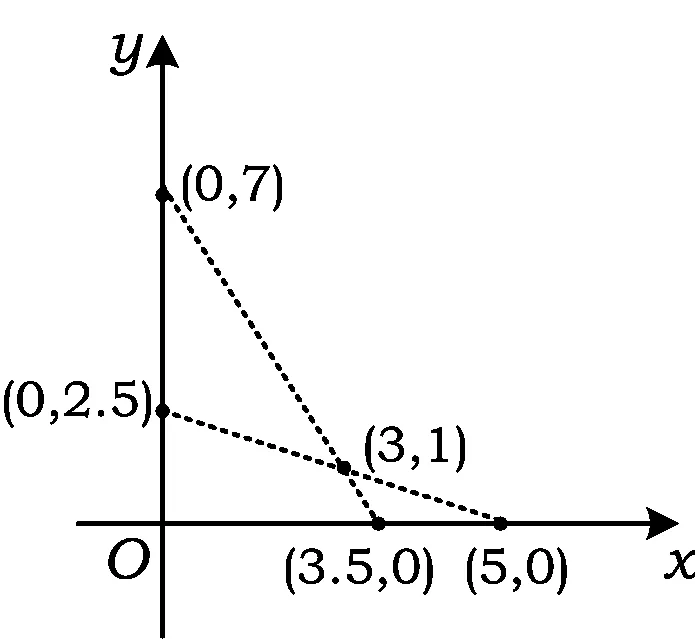
图1
分析该题考查线性规划中的最优问题,与一般题目的区别是x与y均取整数.如图1所示,可画出不等式所在的区域,不难看出3x+4y在(4,1)处取到最小值.故选B.
点评此类整点问题常可采用网格法(直角坐标系下画出网格)、平移调整法(平移至对应的最优位置)、估算法(取一些特殊量进行计算)得到正确的结论.
2 方程类
方程类问题通常与方程有关,针对不同的问题,如何进行合理转化是关键,往往先要了解求根的过程,然后再去挖掘解决问题的方法.
例4设n∈N+,一元二次方程x2-4x+n=0有整数根的充要条件是n=________.
(2011年陕西省数学高考理科试题)
分析该方程要求整数根,且方程的各个系数均为整数,故判别式必须为完全平方数才可能成立.可直接利用求根公式进行计算,然后用完全平方数与整除进行判断和计算.
解由求根公式得
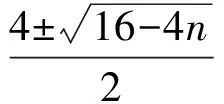
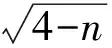
又因为n∈N+,可取n=1,2,3,4,验证可知,n=3,4符合题意;反之当n=3,4时,可推出一元二次方程x2-4x+n=0有整数根.故所求n的值为3,4.
变形已知函数f(x)=ax2+(4a+2)x+4a-6,则使函数f(x)至少有一个整数零点的所有正整数a的值之和等于
( )
A.8 B.20 C.26 D.28
(该题除了采用例4的方法之外,还可用数形结合、反解a求x的范围等方法求解.)
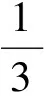
(1)如果g(x)=f′(x)-2x-3在x=-2处取得最小值为-5,求f(x)的解析式;
(2)如果m+n<10(m,n∈N+),f(x)的单调递减区间的长度是正整数,试求m和n的值(注:区间(a,b)的长度为b-a).
(2011年江西省数学高考文科试题)
分析第(1)小题略.第(2)小题的实质是f′(x)=0的2个实数根的差为整数,但不等价于2个根为整数,故求解中不能混淆.
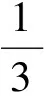
f′(x)=x2+2mx+n<0.
由于递减区间的长度是正整数,故可设f′(x)=x2+2mx+n=0的2个实数根为a,b(b>a),由韦达定理得
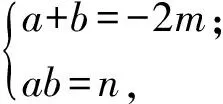
区间长度
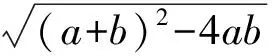
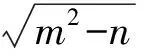
因为m,n∈N+,m+n<10,且b-a为整数,所以

点评求解此类问题的关键是抓住方程根的思想,满足整数所需条件该如何进行转化,结合平时所学整数解的有关方法进行解答.
3 条件类
条件类问题所给条件中的一些量是整数,要求在解答过程注意量所取的范围,有时正因为条件的特殊性,使问题得以简化.
例6命题“所有能被2整除的整数都是偶数”的否定是
( )
A.所有不能被2整除的数都是偶数
B.所有能被2整除的整数都不是偶数
C.存在一个不能被2整除的数都是偶数
D.存在一个能被2整除的数都不是偶数
(2011年安徽省数学高考理科试题)
分析该题考查全称命题的否定.把全称量词改为存在量词,并把结果否定.故选D.
例7设S是整数集Z的非空子集,如果任意a,b∈S有ab∈S,则称S关于数的乘法是封闭的.若T,V是Z的2个不相交的非空子集,T∪V=Z且任意a,b,c∈T,有abc∈T;任意x,y,z∈V,有xyz∈V,则下列结论恒成立的是
( )
A.T,V中至少有一个关于乘法是封闭的
B.T,V中至多有一个关于乘法是封闭的
C.T,V中有且只有一个关于乘法是封闭的
D.T,V中每一个关于乘法都是封闭的
(2011年广东省数学高考理科试题)
分析该题主要考查基本逻辑、推断能力,可用排除法判断.故选A.
例8设m,k为整数,方程mx2-kx+2=0在区间(0,1)内有2个不同的根,则m+k的最小值为
( )
A.-8 B.8 C.12 D.13
(2011年重庆市数学高考理科试题)
分析该题前半部分考查二次方程根的分布为主,后半部分考查类似于线性规划中的整点问题.
解由题意得到下列不等式组
且m,k为大于0的整数,求m+k的最小值.可利用整点类问题的求解方法进行解答.余下部分略,答案为D.
例9某学校要招开学生代表大会,规定各班每10人推选1名代表,当各班人数除以10的余数大于6时再增选1名代表.那么,各班可推选代表人数y与该班人数x之间的函数关系用取整函数y=[x]([x]表示不大于x的最大整数)可以表示为
( )

(2010年陕西省数学高考理科试题)
分析该题的关键是取整的处理.
方法1特殊值法.令x=56,y=5,排除选项C,D;令x=57,y=6,排除选项A.故选B.
方法2设x=10m+α(0≤α≤9).
当0≤α≤6时,
当6<α≤9时,
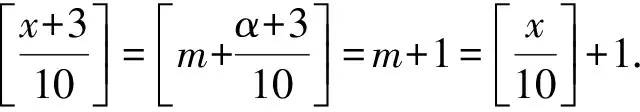
点评求解此类问题的关键是如何对不可忽视的条件进行转化和应用.这类题目可利用条件的特殊性(整数)取特别元素进行判断,故常可用排除法求解.
在本文中例举的高考整数类问题只是一个契机,关键是从高考卷中去发现问题,找出试卷的共鸣点,为今后的高考复习提供一个新的方向,但切不可盲目地去挖掘,要做到不离教材,不离大纲.
