网架结构变形的灰色预测

吕彩忠，廖小辉，胡云世

（衢州学院 建筑工程学院，浙江 衢州3240000）

网架结构受到风载荷、温度和湿度变化、挤压等因素影响时，都会产生变形。为了可靠判定网架结构的变形是否安全，对网架结构进行变形观测是非常有必要的。笔者以衢州学院图书馆结构为例，在对网架结构进行大量观测的前提下，采用理论分析与实践相结合的方法，研究采用灰色理论对观测数据进行分析和预测的可靠性。

衢州学院图书馆由2座主楼构成（图1），而连接2座主楼的结构为网架结构（图2），设计为焊接球网架，用相贯法［1-3］焊接施工成形。该建筑物处于衢州学院校园的南北主轴线上，建筑物高度约为40.5m，总建筑面积约为25 275.9m2。建筑顶面采用L形板面结构，板跨度为65m，宽为15m，板顶标高为39.1m。平面布置如图2所示，网架结构为L形，跨度65m，网架高度1.8～2.0m，网架侧面设计为干挂花岗岩，底板为纯铝板吊顶，屋顶使用彩钢瓦防水。因此，结构的自重较大，为确保结构的稳定性，对建筑物结构进行变形观测显得尤为重要。

1 变形观测

网架施工完成后，为确保工程质量，必须从拆除施工脚手架开始，对网架进行相应的变形观测。为了对网架结构的变形规律有较好的预测，对该网架结构的变形观测点作了如图3的布置，即将监测点均选择为上弦支托顶，测量时基准点位置选在女儿墙顶，并假定基准点标高为±0.000。

采用NLD1-AL332-1型自动安平水准仪，对各点进行为期一周的施工监测，为确保数据准确性和可靠性，每次观测均采用三等闭合水准测量。监测时间为每天上午9：00与下午4：00分别测量2次，测量数据见表1。

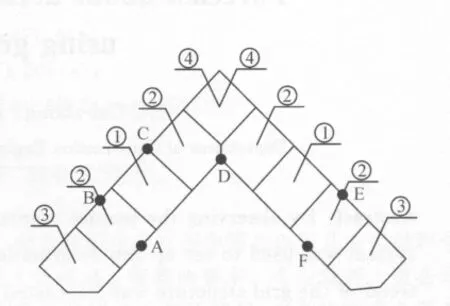
图3 变形观测点布置Fig.3 Arrangement of deformation observation points

2 变形预测

2.1 预测模型的建立

对网架结构的变形观测数据进行分析，可以发现，对结构观测点进行有限次的观测数据，各数据间没有明显的规律，具有不确定性，但其数据变化与时间有关；而灰色理论可以实现对既含有已知信息，又含有不确定信息的系统进行预测，就是对在一定范围内变化的、与时间有关的灰色过程进行预测。由此，建立两者之间的关系，建立 GM（1，1）［4-7］模型：

设时间序列：

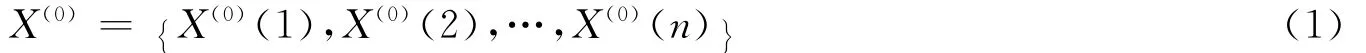
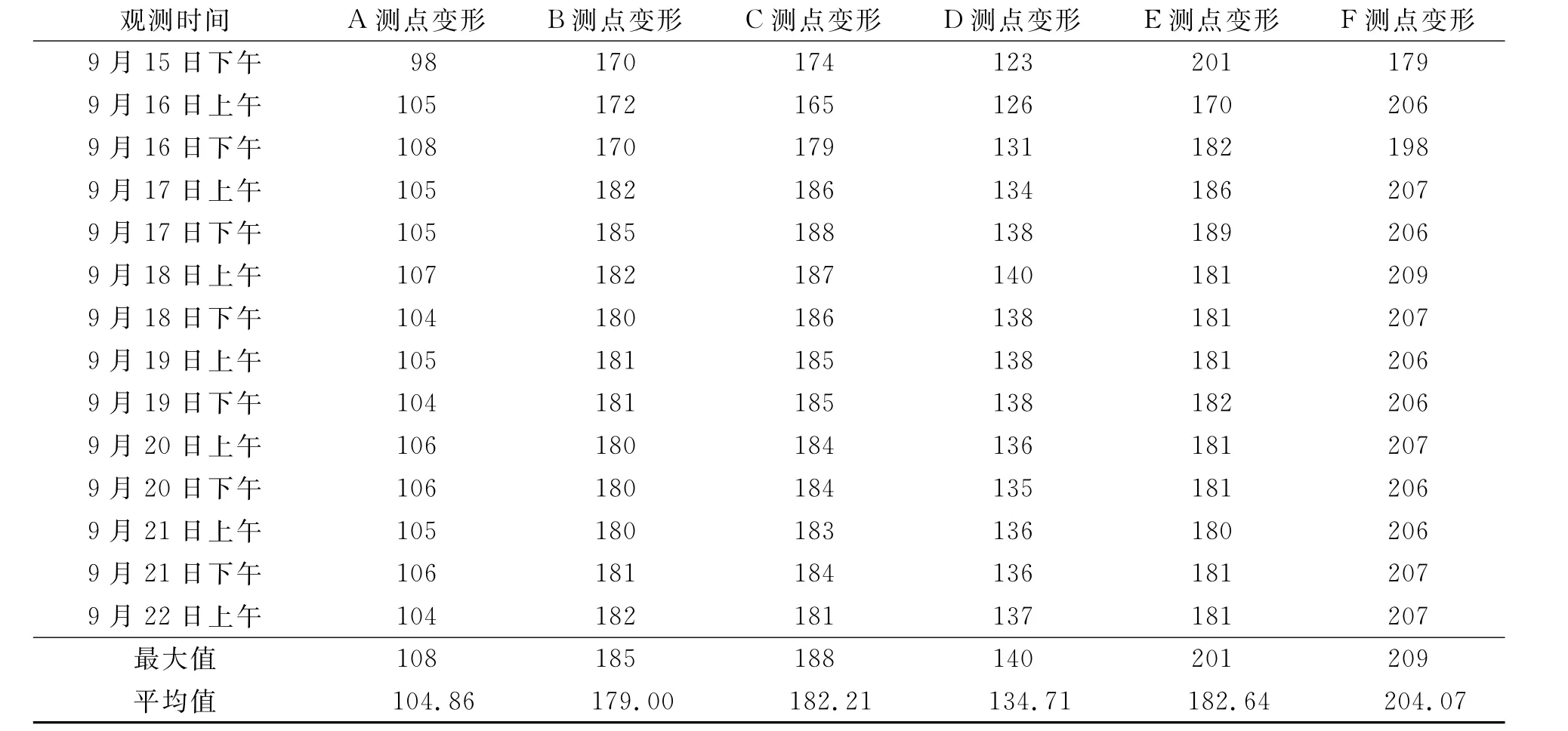
表1 施工拆架观测数据汇总表Table 1 Summary of observational data about stent removal mm

有n个观测值。

通过累加生成新的序列为：

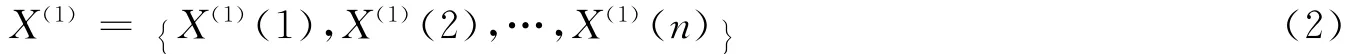
则GM（1，1）模型相应的微分方程为：

式（3）中，α— 发展灰数；μ—内生控制灰数。

设α＾为待估参数向量：

利用最小二乘法求解得：

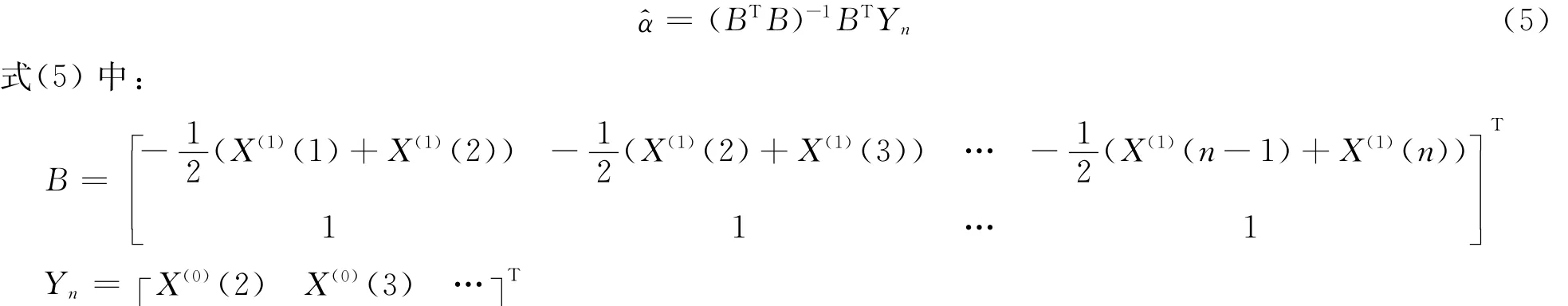
求解微分方程（3），即可得预测模型：

2.2 预测过程

2.2.1 确定原始观测数据序列

该网架结构的各观测点的允许值为325mm，当变形量超过325mm时，结构不安全，由此建立各观测点的观测数据序列，如观测点A的原始序列为：

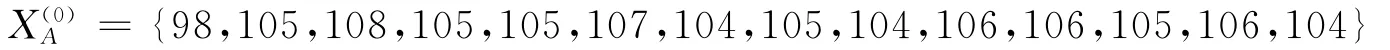
其余观测点数据见表1。

2.2.2 确定原始观测数据序列对应的时刻序列

对网架结构的实际观测时间如表1所示，每次监测的间隔时间为17h，为等时刻监测，因此，将监测时间转变成时间序列，并将各观测点数据累加生成新的序列，如表2所示。

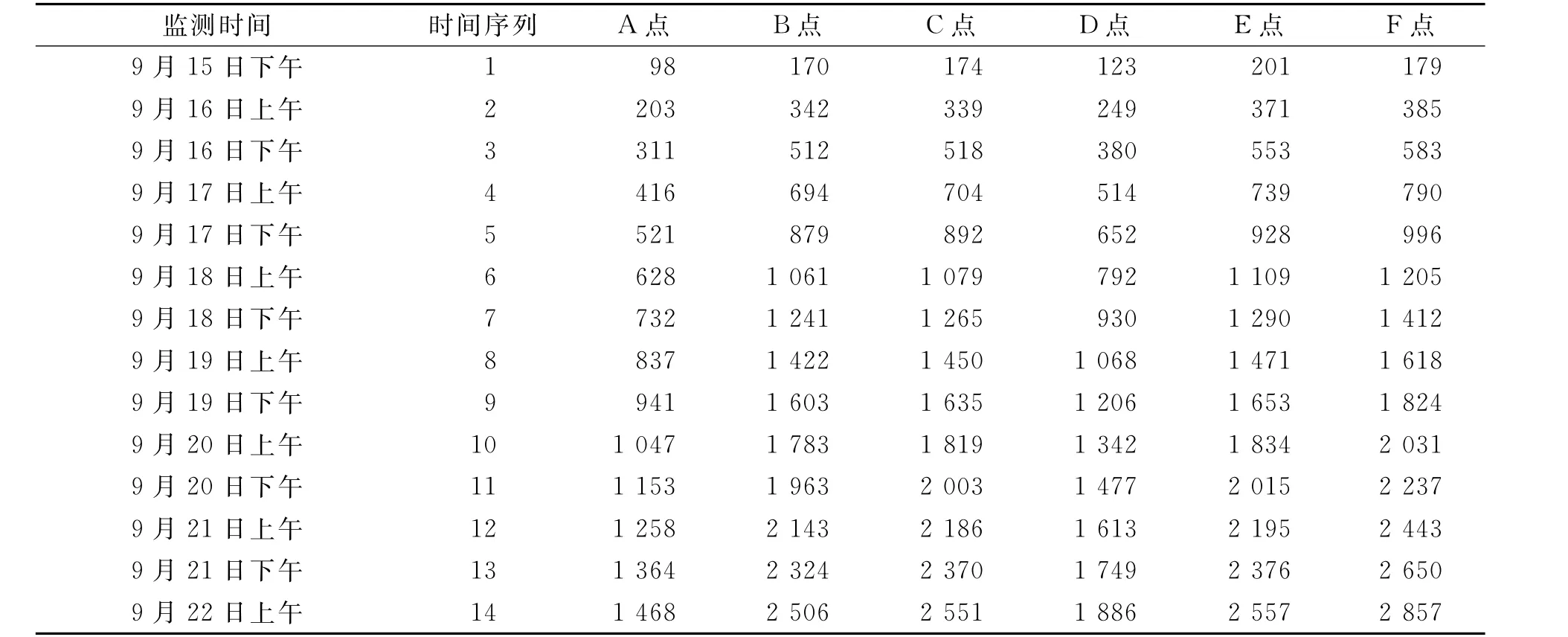
表2 监测时间与时间序列转化表Table 2 Transformation about monitoring time and time sequence mm

2.2.3 建立 GM（1，1）模型

对观测点A：

同理，求得其他各点的α＾值，见表3。

表3 各观测点α＾值Table 3 α＾value of each observation point

2.2.4 预测未来某一时刻的变形值

由式（6）得各观测点的预测模型如下：

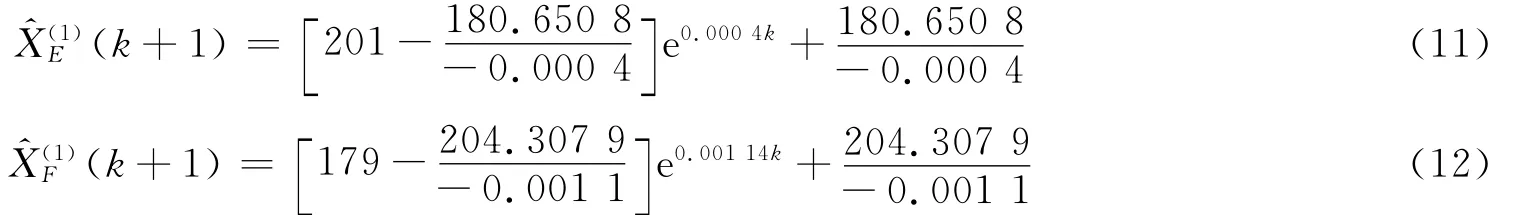
由式（7）～（12）对A～F观测点的变形进行预测，结果见表4。将表4累减运算，得到实际变形预测值，见表5。

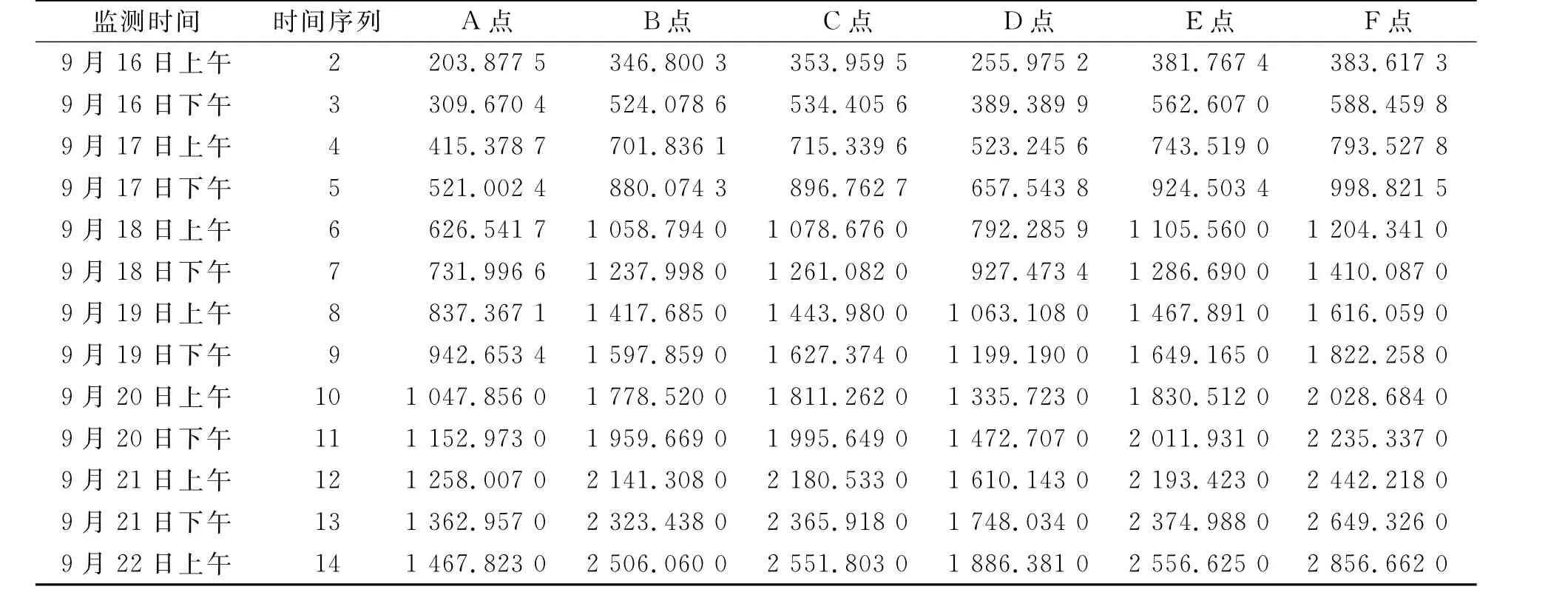
表4 灰色模型预测结果Table 4 Prediction results by grey model mm

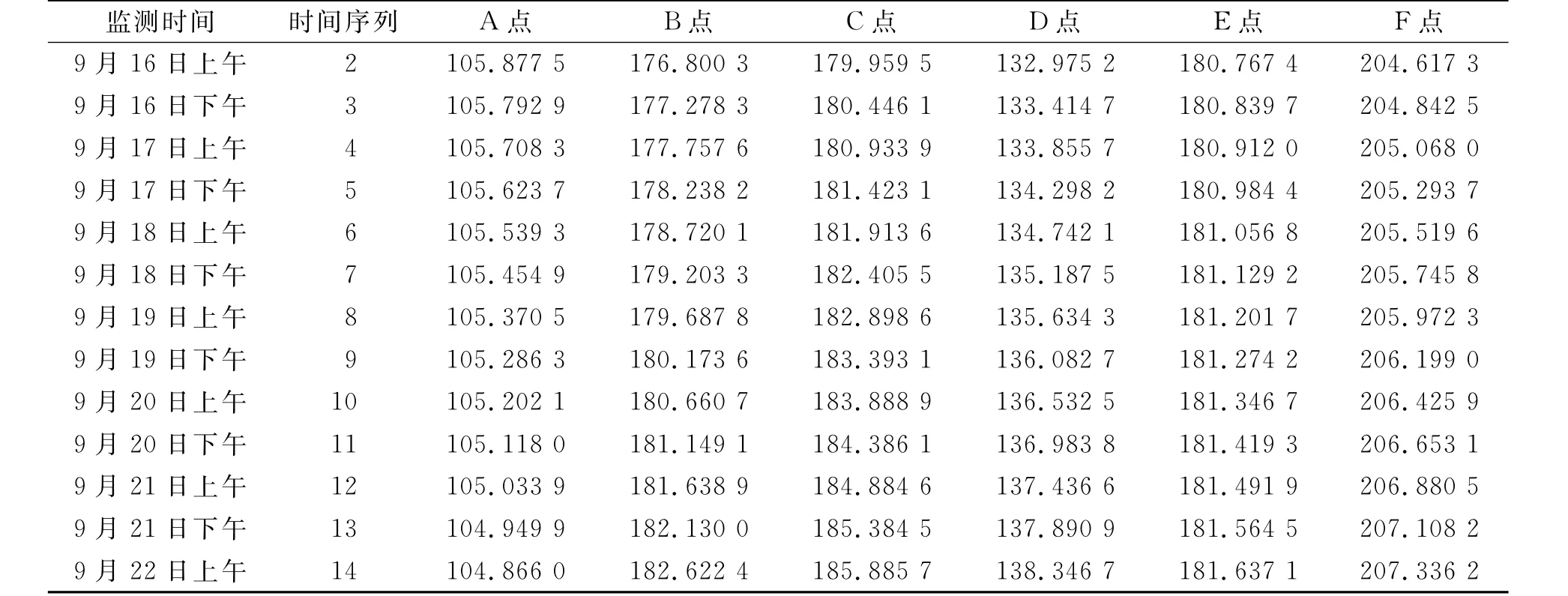
表5 实际变形预测结果Table 5 Prediction results of actual deformation mm

2.3 预测精度检验

为了评价灰色预测理论在网架结构变形观测上的精度，可以采用残差检验［8-10］来校验预测的精度，即按式（7）～ （12）计算出（i），如表4所示，并按式（13）将（i）累减生成了（i），如表5所示，由式（14）求得绝对误差序列，见表6。

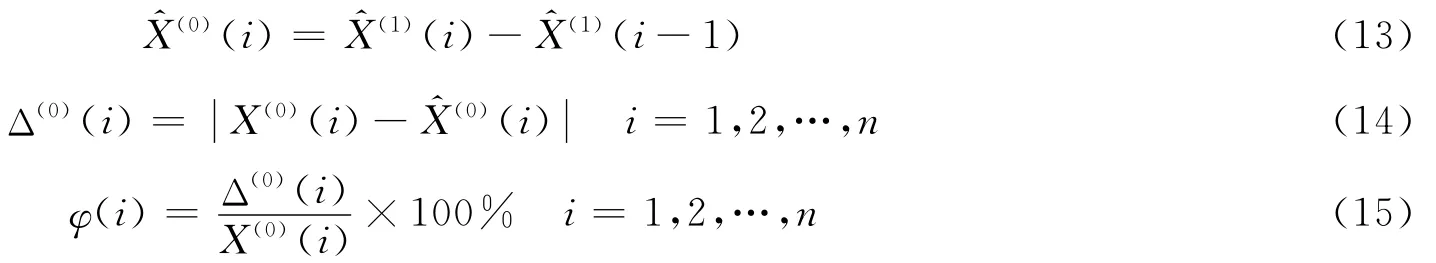
按式（15）可以求得预测结果的相对误差序列，见表6。

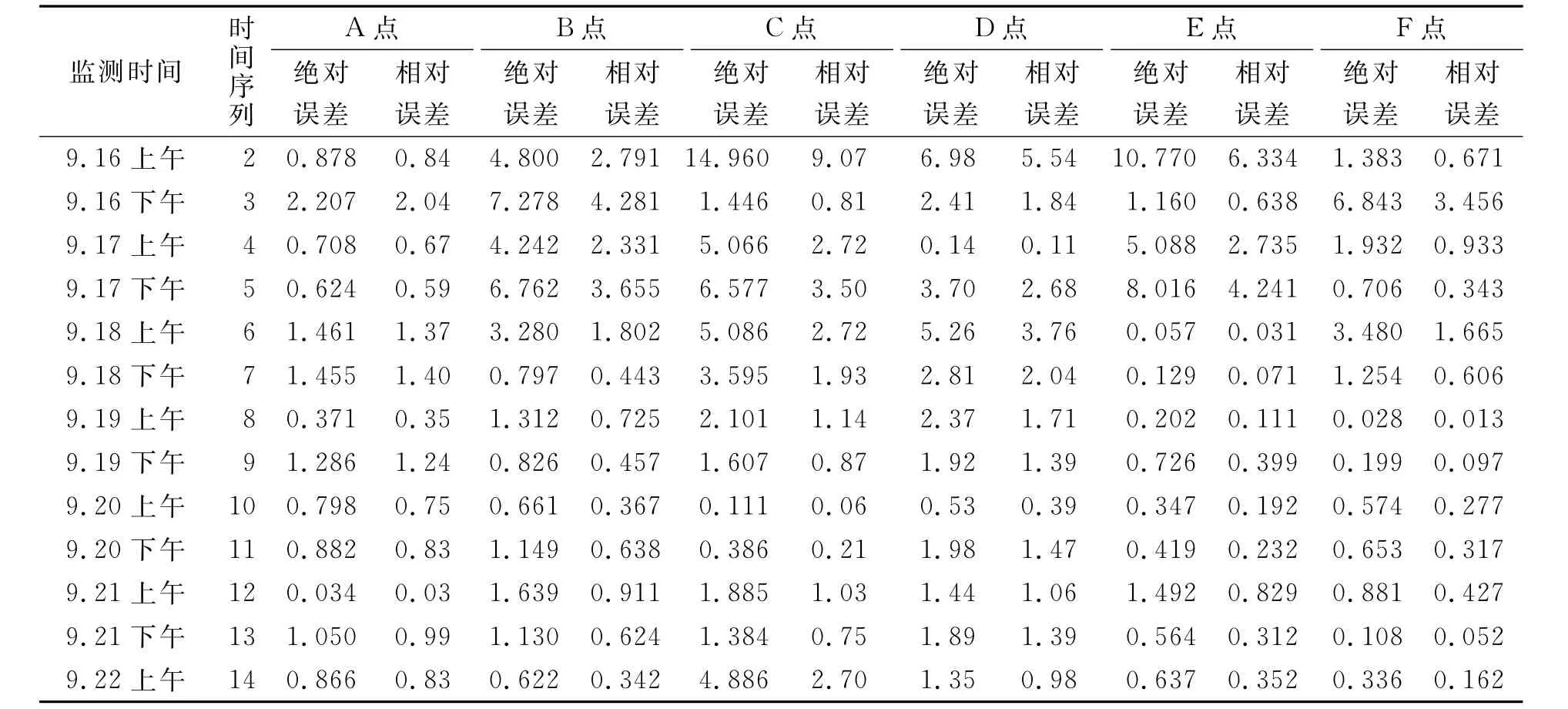
表6 预测结果的误差序列Table 6 Error sequence of prediction results mm

预测数据与实际观测数据对比如图4所示。

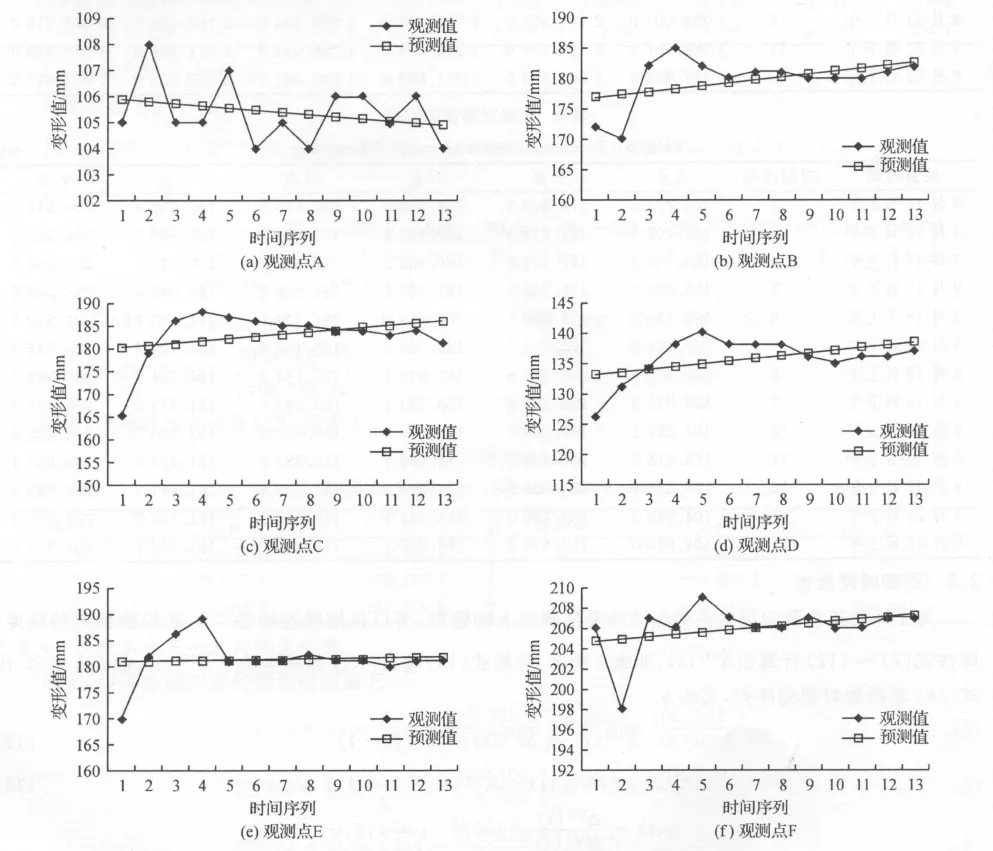
图4 观测数据与预测数据对比Fig.4 Comparison of observational data and prediction data

分析表6与图4可以看出，用灰色理论预测的变形结果与实际观测的变形结果基本吻合，其中9月16日上午观测点C的观测值与预测值相差最大，达到9.07mm，平均相对误差最大值在观测点C处，达到2.1mm。由此可见，灰色理论预测模型适用于网架结构的变形观测。

3 结 语

通过采用灰色理论，对衢州学院图书馆网架结构建立变形预测模型，通过对预测数据的分析，验证了该方法对网架结构变形趋势具有较好的控制作用；利用残差分析来评价网架结构预测模型的精度等级，从理论上证明了灰色理论预测模型在网架结构上的适用性；预测模型采用的原始观测数据为等间隔观测数据，即两次观测间隔时间为17h，网架结构的变形预测模型同样适用于非等时刻观测。该观测方法可以作为一般网架结构变形的灰色预测分析的参考。

［1］ 柳会红，王济川，王海波.组合网架结构的加固分析与处理对策［C］／／柳炳康，吴胜兴，周安.工程结构鉴定与加固改造.长沙：湖南大学出版社，2002：399-402.

［2］ 尹德钰，赵红华.网架质量事故实例及原因分析［J］.建筑结构学报，1998，19（1）：15-23.

［3］ 牛书静，郭海针.螺栓球节点网架加工与安装质量问题的加固处理［J］.河南机电高等专科学校学报，2004，12（4）：31-32.

［4］ 傅立.灰色系统理论及其应用［M］.北京：科学技术文献出版社，1992.

［5］ 易德生，郭萍.灰色理论与方法：提要、题解、程序、应用［M］.北京：石油工业出版社，1992.

［6］ 袁嘉祖.灰色系统理论及其应用［M］.北京：科学出版社，1991.

［7］ 高翥.基于灰色系统的桥梁长期变形预测研究［J］.公路交通技术，2011（4）：84-87.

［8］ 杨瑞波，陈建宏，郑海力，等.残差修正 GM（1，1）模型在煤矿事故预测中的应用［J］.矿业研究与开发，2011，31（1）：73-76.

［9］ 李博峰，沈云中.基于等效残差积探测粗差的方差-协方差分量估计［J］.测绘学报，2011，40（1）：10-14，32.

［10］ 牛连强，冯海文，吴澎.利用残差控制的快速圆弧生成与反走样算法［J］.计算机辅助设计与图形学学报，2011，23（2）：232-239.