平面第二类曲线积分的一种简便计算方法

李小梅

（浙江科技学院 理学院，杭州310023）

第二类曲线积分的计算在微积分学中是一个难点，其中概念既多又抽象，计算既繁又难以判断。如计算时须考虑积分曲线为开曲线或者是闭曲线时的状态，与积分路径有关或无关时的性态，被积函数的偏导是否在区域D内连续还是不连续的条件，曲线是否为正向还是反向时的确定等［1-3］，这些情况在计算第二类曲线积分都必须进行分析。而这些分析恰恰是曲线积分中难以掌握的，特别在研究生入学考试的命题中，曲线积分的出题率很高，而难度系数却又很大，直接导致了较低的解题正确率［4］。本文利用格林公式进行转化，推出了平面上第二类曲线积分计算的一种简便方法，它无需更多的判断就可直接进行计算。

1 准备知识与命题

设曲线L是平面上一条光滑的曲线弧，P（x，y）、Q（x，y）在曲线L上连续。则有：

引理1.1（格林公式） 设闭区域D由分段光滑的曲线L围成，函数P（x，y）及Q（x，y）在D上具有一阶连续偏导数，则有

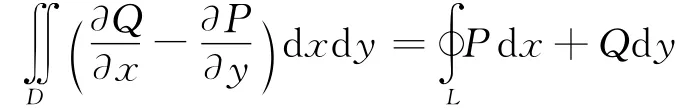
其中L是D的取正向的边界曲线。

引理1.2（曲线积分性质） 设L是有向曲线弧，-L是与L方向相反的有向曲线弧，则

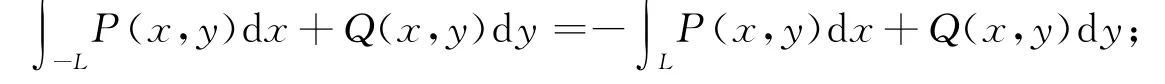
引理1.3 设L为平行X 轴的一条线段，A（x0，y1）为起点，B（x1，y1）为终点，则

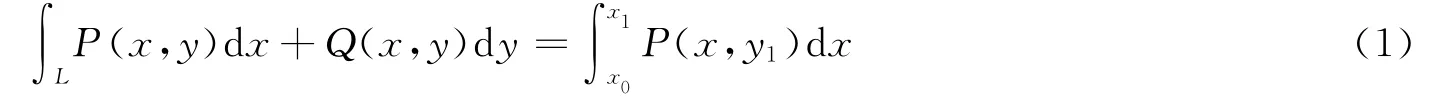
同样，若L为平行Y 轴的一条线段，A（x0，y0）为起点，B（x0，y1）为终点，则有：

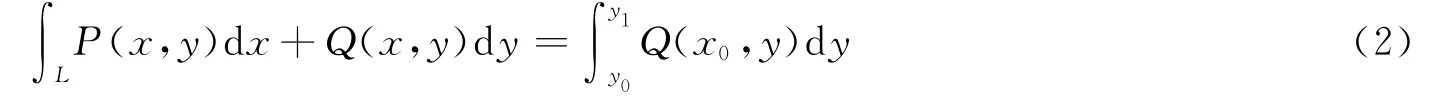
证明：略。

根据以上引理，本研究推出以下结论：

定理1.1 设开区域D是一个单连通域，函数P（x，y）及Q（x，y）在D内具有一阶连续偏导数，则有：

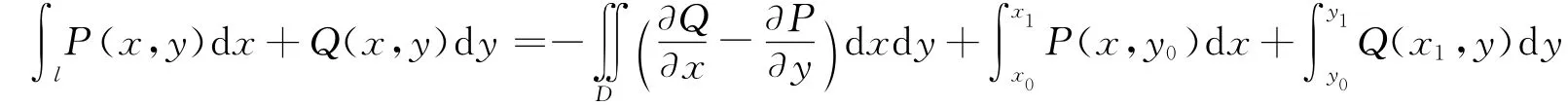
其中曲线l是起点为A（x0，y0），终点为B（x1，y1）（x0＜x1，y0＜y1））区域D 内的一条开曲线。

定理1.2 设闭区域D由分段光滑的曲线L围成，若O（0，0）∈D，且函数P（x，y）及Q（x，y）在D上除O（0，0）外具有一阶连续偏导数，则有：

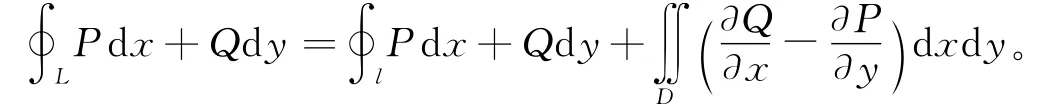
其中L是D的取正向的边界曲线；l是以原点为圆心，半径为r取逆时针方向的边界曲线。

定理1.3 设闭区域D由分段光滑的曲线L围成，且设L为封闭正向曲线，函数P（x，y）或Q（x，y）在曲线L中点B的邻近无界（或称其点为P（x，y）或Q（x，y）的一个奇点）。如果对曲线L上除点B外的任意点处函数P（x，y）及Q（x，y）在D上均有一阶连续偏导数，则当积分∮LP（x，y）d x＋Q（x，y）d y收敛时，有：

这次听众很少，人们不相信青山。村人天生容易失望，每个人容易失望。每个人觉得完了！只有老赵三，他不失望，他说：

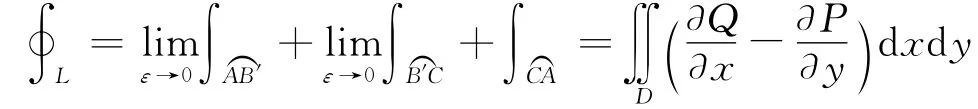
图1 开曲线构成图Fig.1 For mation diagram of open curve

2 定理分析与证明

定理1.1证明 设开区域D是一个单连通域，函数P（x，y）及Q（x，y）在D内具有一阶连续偏导数。曲线l的起点为A（x0，y0），终点为B（x1，y1）（A，B为区域D 内两点且x0＜x1，y0＜y1），连接AC，CB构成封闭曲线L＝l-＋AC＋CB（AC平行x轴，CB平行y轴；且L是D的取正向的边界曲线，如图1所示。

由引理1.1：

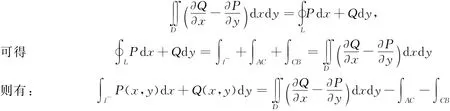
由引理1.2：

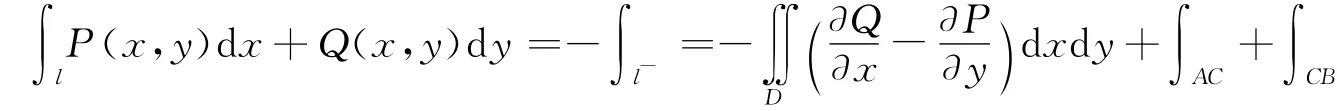
所以根据引理1.3有：

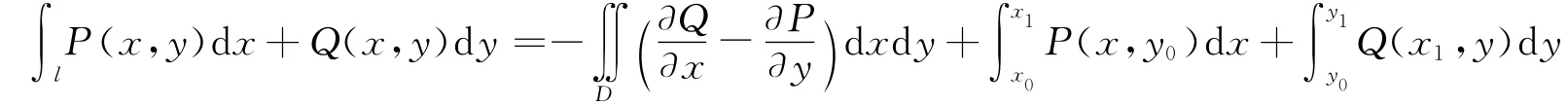
特别是当x0＝x1，y0＜y1时：

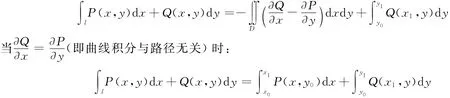
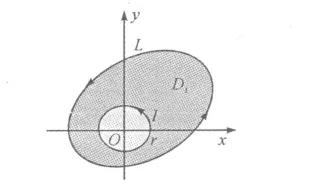
图2 原点在闭曲线内Fig.2 Orignial point inside closed curve

证毕。

定理1.2证明 设闭区域D由分段光滑曲线L围成，当（0，0）∈D时，作位于D内圆周l：x2＋y2＝r2，如图2所示。

记D1由L和l所围成，应用格林公式，得

定理1.3证明 先给出定义：设L为一条光滑或分段光滑的封闭正向曲线，函数P（x，y）或Q（x，y）在曲线L中点B的邻近无界（或称其点为P（x，y）或Q（x，y）的一个奇点）。如果对曲线L上除点B 外的任意点处函数P（x，y）及Q（x，y）在D上均有一阶连续偏导数，取B（b1，b2）点邻近点B′（b1＋ε，b2敛的；如果上述有一个极限不存在，则称积分是发散的。因此，当积分∮LP（x，y）d x＋Q（x，y）d y收敛时，显然有

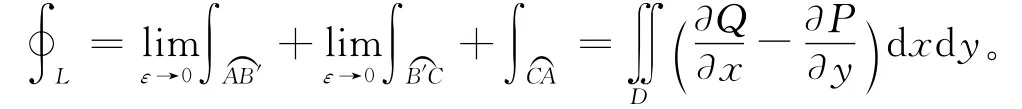
注：对于积分曲线为封闭曲线时，定理1.2、1.3分别讨论了封闭曲线L包含原点和经过原点O（0，0）且函数P（x，y）及Q（x，y）仅在O（0，0）处不连续（此时曲线积分就是文献［5］中所定义的无界函数广义第二类曲线积分）时的两种情况。至于函数P（x，y）及Q（x，y）在封闭曲线所围的闭域D上具有一阶连续的偏导数，则按格林公式做。

3 举 例

上面定理是分平面第二类曲线积分为开曲线还是闭曲线两种类型进行讨论的。因此，在应用上面定理时，首先考察曲线是开曲线还是闭曲线，再分别应用上述定理即可（以下例题均假设满足定理条件，题中不再说明）。

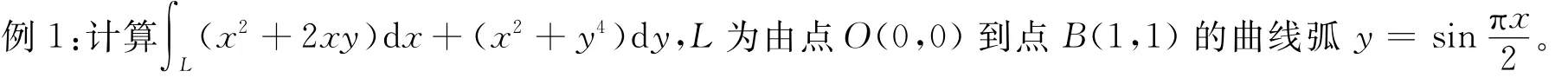
分析：按照平常方法计算有1）参数法［1］，但较难；2）判断与路径无关，需考虑添加辅助线［6］。由于此曲线为开曲线，且起点O（0，0），终点B（1，1），其中x0＝0＜x1＝1；y0＝0＜y1＝1，满足定理1.1的条件，直接用定理即可。

分析：此积分路径虽然是两段曲线相加的，但仍为开曲线。只要找到起点O（0，0），终点B（0，2），且起点的x，y坐标分别≤终点的x，y坐标，可用定理1.1。

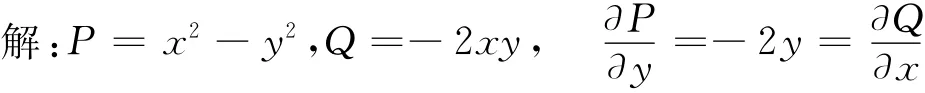
于是，据定理1.1有：

分析：此曲线为开曲线。但此积分路径起点A（a，0），终点O（0，0），起点的x，y坐标分别 ≥ 终点的x，y坐标，不能直接应用定理1.1，可先计算

图3 积分路径图Fig.3 Diagram of integral route

解：因为

由定理1.1公式：

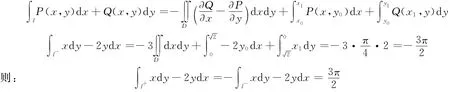
例5：设在上半平面D＝｛（x，y）｜y＞0｝内，函数f（x，y）具有连续偏导数，且对任意t＞0的都有f（tx，ty）＝t-2f（x，y）。证明：对D内的任意分段光滑的有向简单闭曲线L，都有（x，y）dx-xf（x，y）dy＝0。

证明：由于函数f（x，y）在上半平面D＝｛（x，y）｜y＞0｝内具有连续偏导数，且

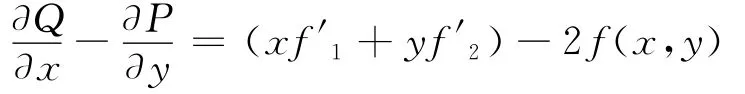
由f（tx，ty）＝t-2f（x，y）两边对t求导可得：

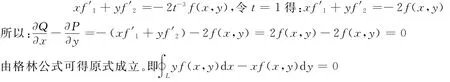
解：1）当x2＋y2≠0时，利用格林公式有

2）当（0，0）∈D 时：利用定理1.2得：

例7：计算上题。其中积分路径为：L1：y＝x2，L2：y＝1，L3：x＝0所围的闭曲线L。

分析：此为闭曲线，且积分路径经过原点，按定理1.3做。

解：取曲线L为正向曲线，

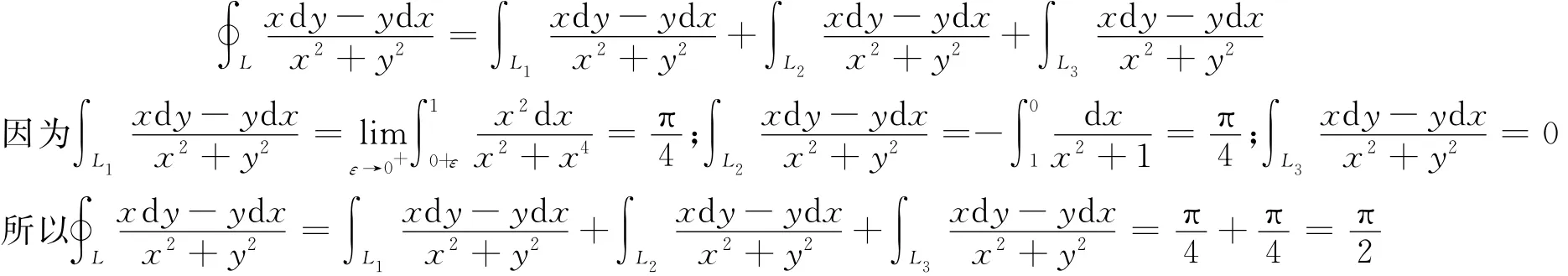
4 结 语

综上所述，利用上述定理计算平面第二类曲线积分时，无需更多的考察曲线是否与路径无关，是否取正向、反向，是否需要添加辅助线。也无需更多地考虑积分曲线方程是否复杂，以免代入后产生的计算繁琐。采用此定理时，只需先观察曲线是开曲线还是闭曲线，然后按照定理的条件、结论计算即可。但由于此定理主要是由格林公式推导而来的，故牵涉到将平面第二类曲线积分的计算转化为平面区域上的二重积分的计算，如果二重积分易计算，则此方法就更显示出其优越性。

［1］ 同济大学数学系.高等数学：下册［M］.6版.北京：高等教育出版社，2007：191-213.

［2］ 吴赣昌.高等数学（理工类）：下册［M］.北京：中国人民大学出版社，2007：104-118.

［3］ 李润菁.探讨曲线积分问题的求解方法［J］.宁德师专学报：自然科学版，2010（4）：410-413.

［4］ 梁存利.高数考研中有关曲线积分问题的求解方法［J］.科技资讯，2009（36）：156-157.

［5］ 王淑兰，王洪林.积分路径上含有孤立奇点的第二类曲线积分［J］.河北工程技术高等专科学校学报，2002（1）：44-48.

［6］ 冯烽.平面第二型曲线积分的解题思路与计算技巧［J］.高等数学研究，2010（2）：34-36.