高压下尾矿材料幂函数型摩尔强度特性研究

刘海明，杨春和，张 超，冒海军，曹 净

（1.中国科学院武汉岩土力学研究所 岩土力学与工程国家重点试验室，武汉 430071；2.昆明理工大学 建筑工程学院，昆明 650500）

1 引 言

材料的强度准则[1]是用以判断材料是否达到弹性极限而即将出现塑性的判据。自20世纪以来，关于土体强度理论一直是土力学研究的基本问题之一。Coulomb在 1773年提出了最大剪应力破坏准则；Mohr提出材料的破坏取决于剪应力和滑移面上的正应力，可用函数表示为：τf=f(σf)。在某些条件下，该曲线可用线性关系τf=c+σftanφ 表示，即常用的直线型Mohr-Coulomb强度理论。对岩土体而言，直线型Mohr-Coulomb强度理论往往只对一定范围下的应力水平适用，超出该范围后一般需要对其进行修正。

修正的Mohr强度理论主要是将其改为曲线，包括抛物线和双曲线。自Hoek & Brown提出抛物线型经验强度准则以来，也有其他一些研究成果[2－3]，抛物线型Mohr强度准则一般可表示为

式中：σ为法向压应力；τ为剪应力；a、b为材料常数。

双曲线型Mohr强度准则为[4]

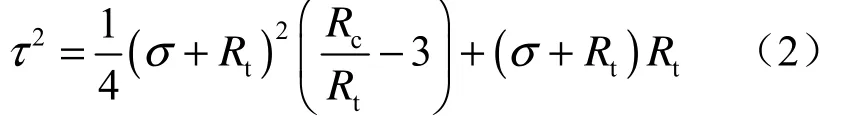
式中：Rt为抗拉强度；Rc为抗压强度。

Mohr屈服面在主应力空间为一不规则的六棱锥面，π平面内为一不等角六边形，角点处的外法线方向存在不惟一性，给数值计算带来困难。Drucker-Prager屈服面在主应力空间为一圆锥面，在π平面内为一光滑曲线，其表述简单且数值计算效率很高，但它不能同时与6个试验点匹配。于是有人研究拉伸试验点与压缩试验点之间的光滑屈服函数，又称为角隅化的强度准则[5]。

修正的抛物线型和双曲线型Mohr强度准则虽可解决传统直线型Mohr-Coulomb强度理论一些不足，能更好地逼近试验曲线，但它们自身亦存在某些缺陷[4]。抛物线型Mohr强度准则由于表达式中剪应力指数为不变参数，造成曲线的弯曲程度调节有限，导致试验数据不能很好地与之吻合；对于双曲线型Mohr强度准则，由于双曲线的一个特性就是有渐近线，造成了高应力条件下剪应力与正应力又近似呈线性变化，与试验数据偏离较大。

尾矿坝是矿业工程中的重要构筑物，是一个潜在的高势能危险源。由于受用地等因素的限制，高尾矿坝不断增加。据统计，截止2008年7月31日，在全国统计的7919座（其中3447座缺乏资料）尾矿坝中，坝高大于100 m的尾矿库有89座；坝高60～100 m的尾矿库有96座。已有的不多的研究[6]表明，高压作用下尾矿砂的内摩擦角比低压下会降低8°～13°。为研究高尾矿坝的稳定性，掌握高压条件下的尾矿材料的强度特性是分析坝体稳定性的基础。

本文通过大量的高压三轴试验研究尾矿材料在高压条件下的强度特性，分析试验前、后的颗分曲线变化特征，建立高压作用下幂函数型Mohr强度准则，研究成果可为高尾矿坝坝体稳定性分析提供理论依据。

2 幂函数型Mohr强度包络线

关于幂函数型Mohr强度包络线，国内外许多学者[4,7－9]都研究过，如图1所示。一般表达形式为

式中：a、n、b为材料常数。S(σ)作为强度包络线，a、n、b须满足以下条件：

（1）众所周知，一切岩土类材料都具有抗剪强度，也就是对于一切σ都应满足：S(σ)≥0，即aσn+b≥0⇒a ≥0且b≥0。

（2）如图 1所示，存在一个非负的常数 t，满足 S(σ=-t)=0，t为材料的抗拉强度，合理的正应力必须满足σ≥-t 。

（3）鉴于S(σ)的导数S′(σ)是内摩擦角φ (σ)的正切值，而φ (σ)又是σ的函数。当σ超过某一值后，φ (σ)随围压的增大而减小，S(σ)是σ的单调递增函数，即：tan(φ (σ))=d Sdσ=anσn-1≥0 ⇒0≤n 。考虑到 Mohr圆及包络线关于σ轴对称，即：φ(σ≡-t)≡π2，因此，内摩擦角的范围为[0,π2)。

（4）根据经典塑性力学理论[10]，合理的强度包络线必须是外凸的，即d2Sdσ2≤0⇒n(n-1)⋅aσn-2≤0⇒0≤n≤1。

（5）设强度包络线上的任意一点(σ,S(σ))，强度包络线S(σ)应该与该点所在的Mohr圆相切，同时不允许与其相交。转化为数学条件有：强度包络线S(σ)上任一点的曲率半径Rf应该大于等于该点的Mohr圆半径Rm，数学表达式如下：

考虑到 S′(σ)≤0，即：

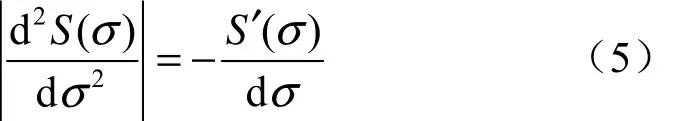
利用式（5），并对式（4）进行三角转换，式（4）可化简为

将幂函数一般通式（3）代入式（6）并化简得

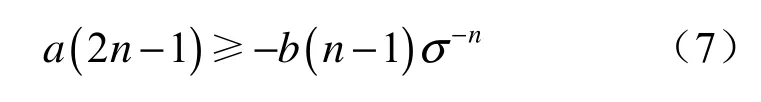
由（1）～（4）条件可得：a≥0、b≥0、0≤n≤1。式（7）等号右边大于等于0；要使式（7）成立，等号左边与σ无关，等号左边也必须大于等于 0，即：a (2 n-1)≥0⇒n≥12。

综上所述，幂函数型Mohr强度通式（3）需满足的条件为：a≥0，b≥0且12≤n≤1。

当n=1时，式（3）退化为直线型 Mohr强度准则，b=c，a=tanφ；当n=12时，式（3）退化为Griffith强度准则，此时a=14Rt，b=-Rt[11]。当12＜n＜1时，幂函数型Mohr强度是直线型Mohr强度与 Griffith强度的组合。大量的研究结果[4,12]表明：幂函数型Mohr强度的幂指数n∈(0.5,1)，从以上分析来看，这是必然的。

3 尾矿材料试验研究

德兴铜矿4号尾矿坝[13]位于德兴铜矿大山选厂以北的西源沟内，为国内及亚洲最大的尾矿坝，设计最大坝高为208 m，2008年7月已堆积了146 m。为了研究该尾矿坝的稳定性，首先必须研究高压条件下尾矿材料的力学特性。现场钻孔勘察取得的400多个原状土样表明，尾矿坝坝顶40 m以下坝体材料主要为尾粉砂及尾亚砂，故本次高压试验研究对象为德兴铜矿4号尾矿坝的尾粉砂和尾亚砂，表1是尾粉砂和尾亚砂的物理指标。

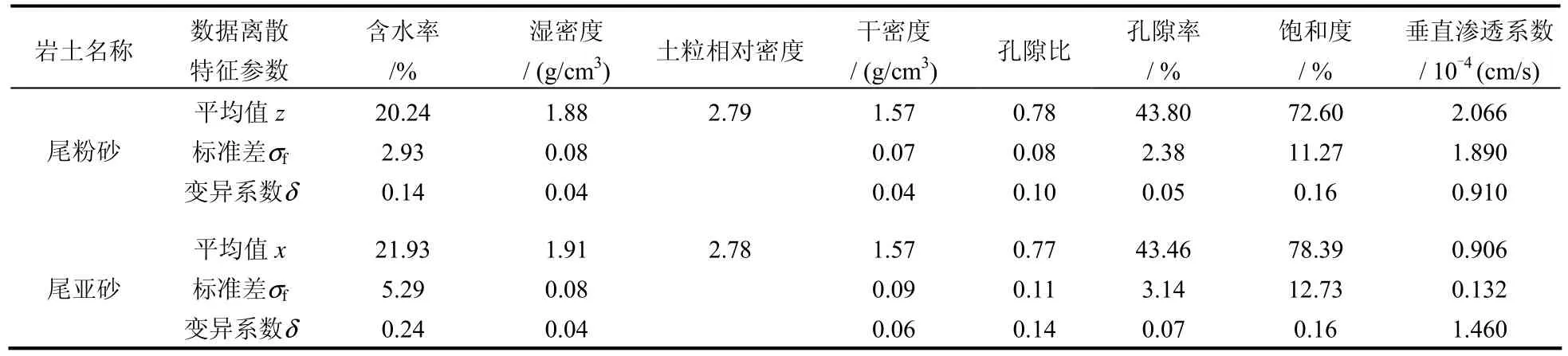
表1 尾矿材料的物理指标参数Table1 Physical parameters of tailings material

高压三轴试验设备采用的是英国 Wykeham Farrance公司生产的三轴仪，最大围压可加到10 MPa，高压三轴试验设备见图2。对于尾矿材料[14－15]，一般将围压在500 kPa以下的试验划为低压试验，将围压高于500 kPa以上的称为高压试验，同时要求对于尾矿堆积高度超过100 m的尾矿坝，必须补充高压试验资料。试验的破坏标准取主应力差与轴向应变曲线上的峰值作为破坏点，无峰值时，取15%轴向应变时的主应力差值作为破坏点。为研究高压作用下尾矿材料的力学性质，试验对尾粉砂、尾亚砂的原状样φ39.1 mm×80 mm在不同围压下（400、800、1200、1600、2000、3000 kPa）进行高压三轴不排水试验，见图3。结果表明：随着围压增大，强度不断递增，但增加幅度不断减小，应力-应变曲线没有明显峰值。

4 尾矿材料幂函数型Mohr准则探讨

4.1 幂函数型Mohr强度准则参数拟合

三轴排水试验可得到破坏时的最小主应力σ3、最大主应力σ1、孔隙水压力u，变换可得：平均应力p=(σ1+σ3)2、平均有效应力 p′=(σ1+σ3-2u)/2、偏应力，由于总应力强度与有效应力强度的参数拟合过程基本相同，只需将p换成p′即可，下面以总应力强度为例，说明幂函数型Mohr强度参数的拟合过程。

图2 高压三轴试验设备Fig.2 High pressure triaxial test equipment

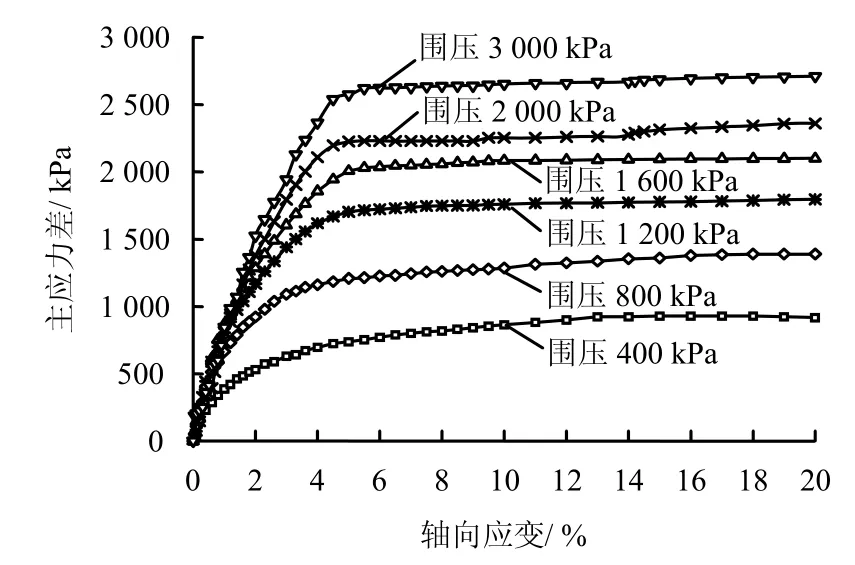
图3 不同围压下高压三轴压缩试验典型曲线Fig.3 Typical stress-strain curves of high pressure triaxial test under different confining pressures

三轴试验结果可用p、q平面的点{pi,qi}i=1…m来表示，由于幂函数型Mohr强度包络线是Mohr平面σ、τ中的一条曲线，为了进行参数拟合，需要先将两者统一，一般可将{p,q}变换至{σ ,}τ，参考图1得

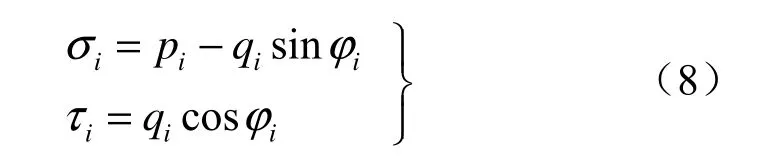
式中：φi为数据点{pi,qi}的内摩擦角。

一般采用迭代法进行参数拟合，定义φi,j-1为{pi,qi}的第j-1次迭代的内摩擦角，参数拟合过程如下：

（1）取 φi=φi,j-1，用式（8）计算得到数据点{σi,τi}i=1…m。

（2）采用式（3）对数据点{σi,τi}i=1…m进行曲线拟合，并由式（9）确定最优的拟合参数{aj,nj,bj}。

拟合参数a、n、b必须满足如下条件：a≥0，12≤n≤1，b≥0。

（3）采用最优的拟合参数{aj,nj,bj}重新计算内摩擦角φi,j=arctan(ajnjσnj-1)。

重复步骤（1）～（4），直到 (Δ φmax)j满足要求为止。通常，初始的内摩擦角φi,0未知，可设为直线型Mohr强度的内摩擦角。

4.2 尾矿材料幂函数型Mohr强度准则研究

尾矿材料高压三轴不排水试验的幂函数型Mohr包络线以及包络线的拟合如图4及表2所示。研究结果表明：无论是总应力强度包络线还是有效应力强度包络线，幂函数型Mohr强度准则都可以较好地反应尾矿材料在高压条件下的强度特性。

高压条件下尾矿材料的试验结果表明：抛物线型和双曲线强度准则虽然解决了传统直线型 Mohr-Coulomb强度准则的一些不足，但仍不能很好地体现尾矿材料在高压力作用下强度的弱化特征。本文建议采用幂函数来拟合强度包络线，结果表明：当围压大于等于800 kPa时，幂函数型Mohr包络线能较好地与试验结果吻合，但当围压低于800 kPa时，误差较大。

5 高压下尾矿材料的颗粒破碎效应

颗粒破碎[16]是指岩土颗粒在外部荷载作用下产生结构破坏或破损，分裂成粒径相等或不等的多个颗粒的现象。颗粒破碎[17－18]既与岩土体颗粒本身的物理力学性质有关，如颗粒的粒径、颗粒级配、表面粗糙程度、形状、矿物成分等；同时还与应力状态、应力路径、加载速率等有关。颗粒破碎会引起岩土体级配的改变，一般可通过试验前、后级配曲线的变化来研究颗粒破碎效应。

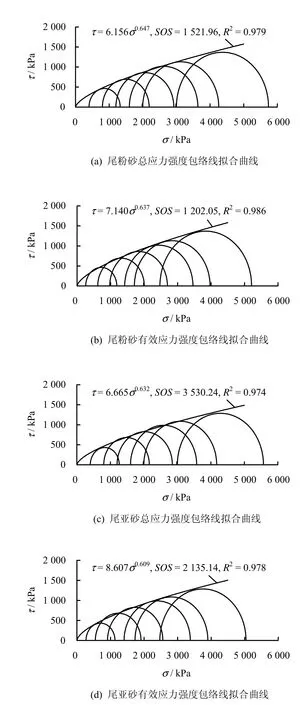
图4 高压下尾矿材料幂函数型Mohr强度包络线Fig.4 Power-function strength envelopes of tailings materials under high stress pressures

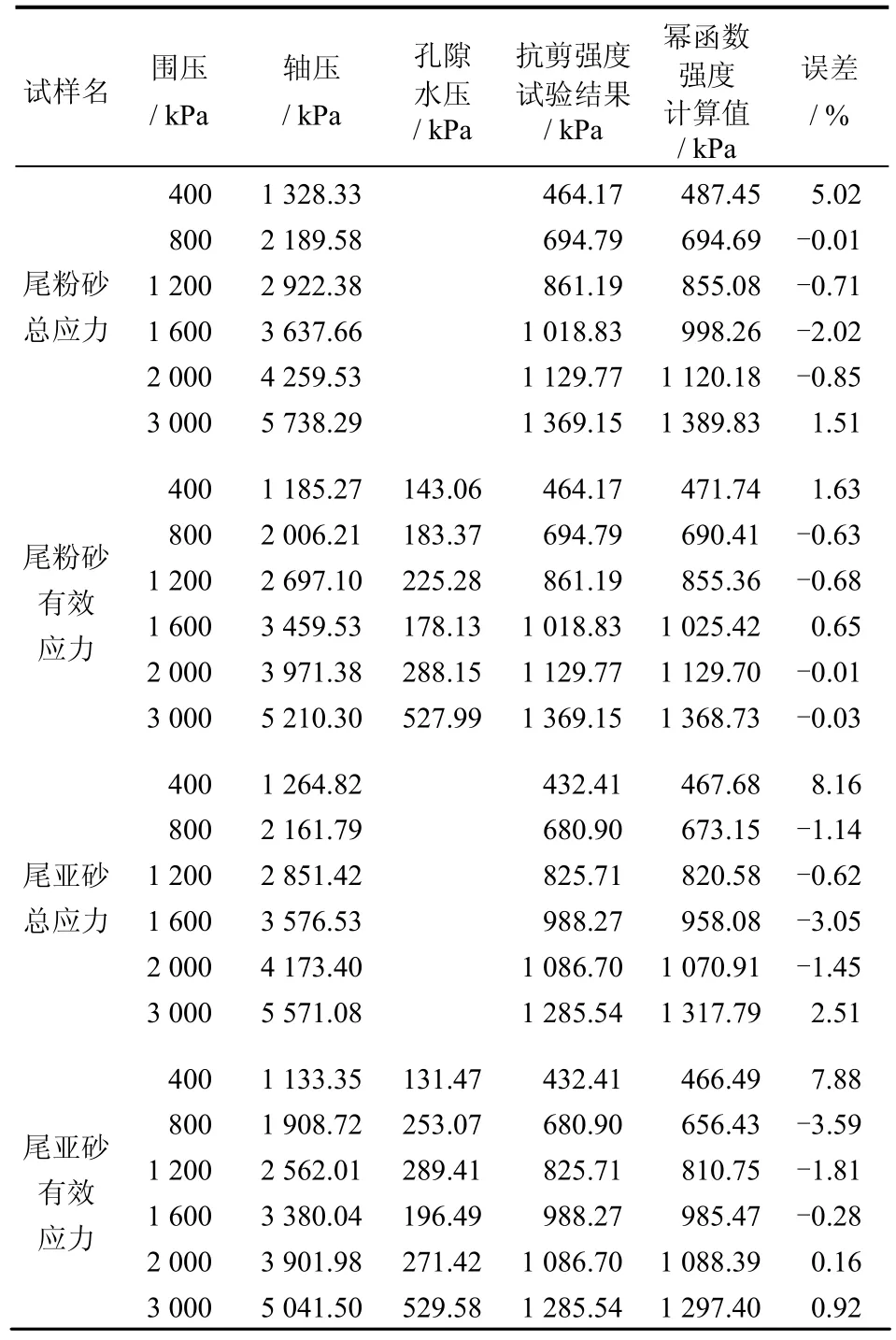
表2 高压下尾矿材料试验结果与幂函数型Mohr强度准则计算结果对比Table2 Comparison of test values and calculation values of power function based on the Mohr strength criterion for tailings material under high pressures

5.1 颗分曲线特征研究

试验前、后颗分结果表明，同一试样在相同压力下不同部位的破碎程度不同，上部比下部破碎程度要大一些。为统一比较，选择试样上部20 mm进行颗粒分析，如图5、6所示。试验表明：

（1）当围压达到某一阈值后，尾矿材料在剪切过程中将发生颗粒破碎，发生颗粒破碎程度与围压大小密切相关，并存在一阈值，只有当围压大于等于该阈值之后，才发生颗粒破碎。对于试验尾粉砂，阈值为1200 kPa；对于试验尾亚砂，阈值为1600 kPa。该阈值大小与试验材料的颗粒尺寸密切相关，初步研究表明，随着尾矿材料颗粒尺寸的减小，阈值增加。殷家瑜等[6]的研究表明：尾矿砂在剪切过程中（排水剪切）即使围压不大也会发生颗粒破碎，该研究成果与本文有一定出入。这可能是由于应力路径或是材料特性所引起的。

（2）当围压达到阈值之后，剪切后颗粒破碎的数量随围压的增大而增大，但增大的幅度却随着围压的增大而逐渐减小。

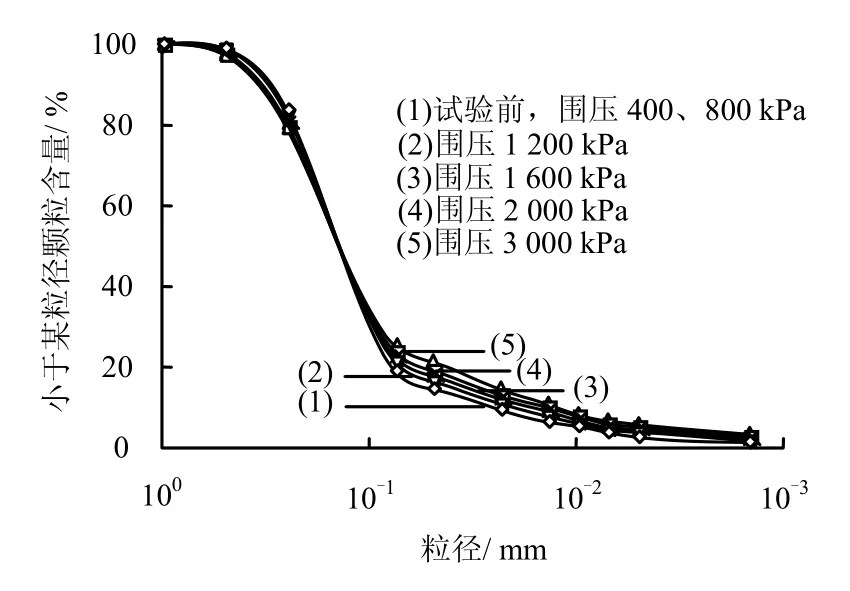
图5 不同围压下尾粉砂试验前、后颗分曲线Fig.5 Grain-size distribution curves of tailings silt under different confining pressures

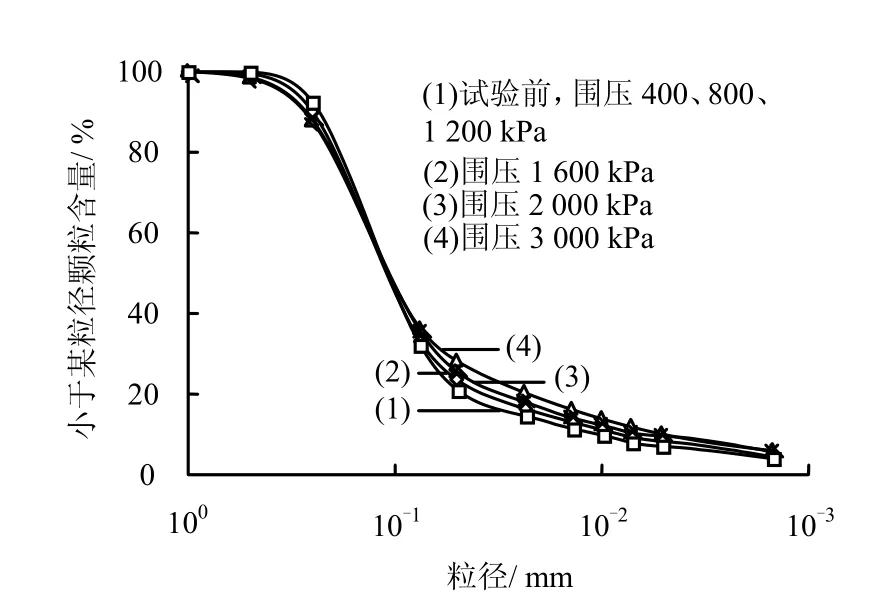
图6 不同围压下尾亚砂试验前、后颗分曲线Fig. 6 Grain-size distribution curves of tailings sub-silt under different confining pressures

5.2 颗粒破碎率研究

目前，对于颗粒破碎程度的度量，工程中主要是以颗粒级配曲线为基础，可分为“单一特征粒径指标”和“多粒径指标”[19]。单一特征粒径指标是以试验前、后某单一特征粒径含量的变化量来衡量颗粒破碎的程度，如采用颗粒粒径d15、控制粒径d60等；多粒径指标以试验前后整个颗粒级配曲线的变化量来衡量颗粒破碎程度，如Marsal采用试验前、后粒组百分含量差的正值之和Bg。

Hardin[20]提出了用相对破碎参量Br来描述颗粒破碎效应，该指标能克服单独考虑某一含量或某一粒径的缺点，能够全面反应颗分曲线在试验前、后的变化。本文根据尾矿材料加载前、后颗分曲线变化特征，采用Hardin建议的指标来研究颗粒破碎，但将Hardin建议的临界颗粒破碎直径d=0.074 mm改为d=0.0015 mm以适合尾矿材料。如图7所示，以试验前、后颗粒分析曲线与d=0.0015 mm竖线3条线所包围的面积为破碎量Bt，将试验前的颗粒分析曲线与d=0.0015 mm竖线所围的面积定义为破碎势Bp，从而定义相对破碎率 Br=Bt/Bp。根据Br的定义，可以分别计算出各个围压下试验后的颗粒破碎情况，结果如表3所示。

图8为尾粉砂在不同深度的相对破碎率，由图可知，上部试样的相对破碎率比下部试样大，随着围压的增大，上部试样与下部试样的相对破碎率之差不断减小。

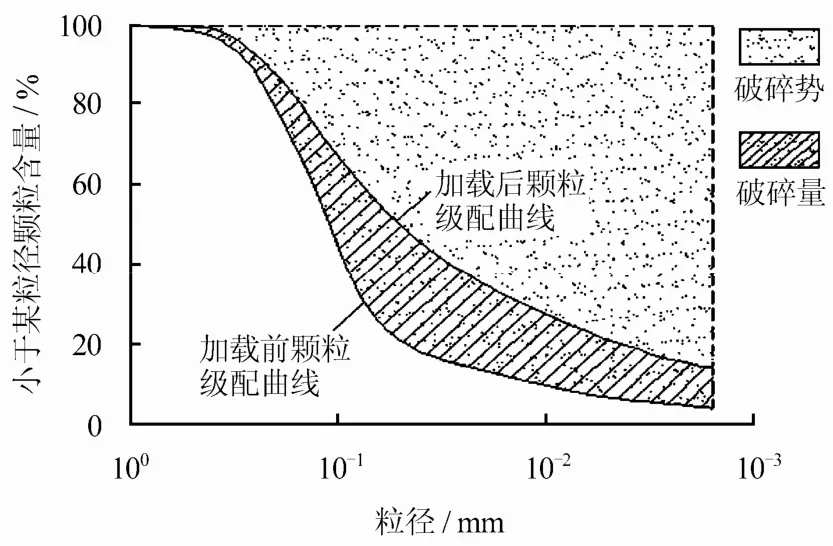
图7 相对破碎率Br的定义Fig.7 Definition of relative-crushing rate Br

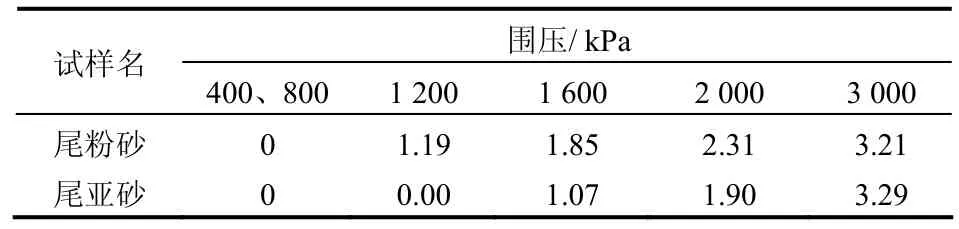
表3 尾矿材料在不同围压下的颗粒相对破碎率(单位: %)Table3 Relative-crushing rate of tailings materials under different confining pressures (unit: %)

图8 尾粉砂在不同分层下的相对破碎率Fig.8 Relative-crushing rate of tailings silt at different layers

6 结论与建议

（1）从理论上推导了幂函数型 Mohr强度通式S (σ)=aσn+b 及其需满足的条件：a≥0，b≥0，≤n≤1。

（2）幂函数型Mohr强度包络线拟合曲线表明：无论是有效应力强度还是总应力强度，幂函数型Mohr强度包络线能较好地体现尾矿材料在高压条件下的强度特性，对于低压作用下（围压小于500 kPa）的尾矿材料，幂函数型Mohr强度理论估算结果偏高，对工程不利，建议低压作用下的尾矿材料仍采用直线型Mohr-Coulomb强度准则。

（3）高压作用下尾矿材料颗分结果表明：当围压达到某一阈值时，尾矿材料在剪切过程中将发生颗粒破碎，该阈值大小与尾矿材料的颗粒尺寸有关，对于德兴铜矿尾粉砂，阈值为1200 kPa；对于铜矿尾亚砂，阈值为1600 kPa。

（4）当围压达到阈值之后，剪切后颗粒破碎的数量随围压的增大而增大，但增大的幅度却随着围压的增大而逐渐减小。

（5）由于尾矿材料的抗剪强度与应力水平密切相关，对于高尾矿坝的稳定性研究，必须通过试验确定所有可能的应力水平范围内的强度参数，建议采取如下步骤：①在试验之前，先用直线型 Mohr-Coulomb强度准则估算强度参数值，再进行初步的稳定性分析，目的是初步确定试验的应力水平；②根据估算的应力水平进行相应的强度试验，采用试验结果重新进行稳定性分析；③将最后分析的应力水平与试验的应力水平进行对比分析，如果两者相差较大，则根据需要补充相应的试验，重新进行稳定性分析，直到满足要求为止。

[1]郑颖人,高红. 材料强度理论的讨论[J]. 广西大学学报(自然科学版),2008,33(4): 337－435.ZHENG Ying-ren,GAO Hong. Discussion of strength theory for materials[J]. Journal of Guangxi University(Natural Science Edition),2008,33(4): 337－435.

[2]赵彭年. 二次抛物线型极限曲线的巷道围岩应力及位移[J]. 有色金属,1979,(1): 41－44.

[3]李顺群,焦学英,王芳. Mohr包线的二次曲线形式[J].辽宁工程技术大学学报,2005,24(6): 853－855.LI Shun-qun,JIAO Xue-ying,WANG Fang. Study of conic for Mohr curve[J]. Journal of Liaoning Technical University,2005,24(6): 853－855.

[4]陈卫忠,刘豆豆,杨建平,等. 大理岩卸围压幂函数型Mohr强度特性研究[J]. 岩石力学与工程学报,2008,27(11): 2214－2220.CHEN Wei-zhong,LIU Dou-dou,YANG Jian-ping,et al.Power function based Mohr strength criterion for marble with unloading confining pressures[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(11):2214－2220.

[5]俞茂宏. 双剪理论及其应用[M]. 北京: 科学出版社,1998.

[6]殷家瑜,赖安宁,姜朴. 高应力下尾矿砂的强度与变形特性[J]. 岩土工程学报,1980,2(2): 1－10.YIN Jia-yu,LAI An-ning,JIANG Pu. Strength and deformation characteristics of tailings under high pressure[J]. Chinese Journal of Geotechnical Engineering,1980,2(2): 1－10.

[7]CHARLES J A,WATTS K S. The influence of confining pressure on the shear strength of compacted rockfill[J].Geotechnique,1980,30(4): 353－367.

[8]YANG Xiao-li,YIN Jian-hua. Linear Mohr-Coulomb strength parameters from the non-linear Hoek-Brown rock masses[J]. International Journal of Non-Linear Mechanics,2006,41(8): 1000－1005.

[9]AL-AJMI AM,ZIMMERMAN RW. Stability analysis of vertical boreholes using the Mogi-Coulomb failure criterion[J]. International Journal of Rock Mechanics and Mining Sciences,2006,43(8): 1200－1211.

[10]陈惠发,萨里普. Elasticity and plasticity[M]. 北京: 中国建筑工业出版社,2005.

[11]李春光,郑宏,葛修润,等. 双参数抛物型 Mohr强度准则及其材料破坏规律研究[J]. 岩石力学与工程学报,2005,24(24): 4428－4433.LI Chun-guang,ZHENG Hong,GE Xiu-run,et al.Research on two-parameter parabolic Mohr strength criterion and its damage regularity[J]. Chinese Journal of Rock Mechanics and Engineering,2005,24(24): 4428－4433.

[12]BAKER R. Nonlinear Mohr envelopes based on triaxial data[J]. Journal of Geotechnical and Geoenvironmental Engineering,ASCE,2004,130(5): 498－506.

[13]张超,冒海军,王光进,等. 德兴铜矿 4号尾矿坝浸润线观测系统的建立及高坝稳定性研究[R]. 武汉: 中国科学院武汉岩土力学研究所,2010.

[14]王风江. 上游法高尾矿坝的抗震问题[J]. 冶金矿山设计与建设,2001,33(5): 10－13.WANG Feng-jiang. Anti-seismic problem of tall tailing dam constructed with upstream method[J]. Metal Mine Design and Construction,2001,33(5): 10－13.

[15]徐志英,沈珠江. 高尾矿坝的地震液化和稳定分析[J].岩土工程学报,1981,3(4): 22－31.XU Zhi-ying,SHEN Zhu-jiang. Liquefaction and stability analysis of a high tailing dam under earthquake excitation[J]. Chinese Journal of Geotechnical Engineering,1981,3(4): 22－31.

[16]张家铭,汪稔,张阳明,等. 土体颗粒破碎研究进展[J].岩土力学,2003,24(增刊2): 661－665.ZHANG Jia-ming,WANG Ren,ZHANG Yang-ming,et al.Advance in studies of soil grain crush[J]. Rock and Soil Mechanics,2003,24(Supp.2): 661－665.

[17]LOBO-GUERRERO S,VALLEJO L E,VESGA L F.Visualization of crushing evolution in granular materials under compression using DEM[J]. International Journal of Geomechanics,ASCE,2006,6(3): 195－200.

[18]赵光思,周国庆,朱锋盼,等. 颗粒破碎影响砂直剪强度的试验研究[J]. 中国矿业大学学报,2008,37(3): 291－294.ZHAO Guang-si,ZHOU Guo-qing,ZHU Feng-pan,et al.Experimental research on the influence of particle crushing on direct shear strength of sand[J]. Journal of China University of Mining & Technology,2008,37(3):291－294.

[19]孔德志,张其光,张丙印,等. 人工堆石料的颗粒破碎率[J]. 清华大学学报(自然科学版),2009,49(6): 795－799.KONG De-zhi,ZHANG Qi-guang,ZHANG Bing-yin,et al. Particle breakage ratio of artificial rockfill materials[J].Journal of Tsinghua University (Science & Technology),2009,49(6): 795－799.

[20]HARDIN B O. Crushing of soil particles[J]. Journal of Geotechnical Engineering,ASCE,1985,111(10): 1177－1192.