帷幕灌浆扩散半径及数值模拟的研究

韩 磊，陈建生，陈 亮

（1.河海大学 岩土工程研究所，南京 210098；2.中交第二公路勘察设计研究院有限公司，武汉 430056）

1 引 言

经过几十多年的发展，我国已在注浆技术方面取得了较大进展，应用范围已遍及矿山、水利、土木、交通等多个工程领域。但由于复杂的地层条件和注浆工程的隐蔽性，因而理论方面的研究相对滞后于实践。

渗透注浆是指在压力作用下使浆液充填土和岩石的裂隙，排挤出空隙中存在的自由水和气体，达到加固或防渗的目的。通常把以钻孔中心为原点的浆液充填范围叫扩散半径。注浆理论就是借助于流体力学和固体力学的知识，对浆液的单一流动形式进行分析，建立扩散半径、压力、流量、注浆时间之间的关系。扩散半径决定着注浆孔的布置和浆液消耗量，也是选择工艺参数、评价注浆效果的重要依据。因此，对浆液在地层中的扩散形态的研究具有重要的意义。

多孔介质渗透注浆理论形成比较早，典型代表主要有球形扩散公式和柱形扩散公式。后人多在此基础上进行改良和发展。1938年 Maag[1]推导出牛顿浆液在砂层的球形扩散公式

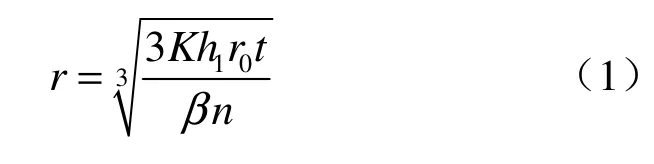
式中：r为浆液的渗透半径；K为土体的渗透系数；h1为注浆压力水头；β为浆液黏度与水的黏度之比，β=μg/μw；n为土体的孔隙率；t为注浆时间；r0为注浆孔半径。

另外还有柱形扩散公式如下[1]：

分析以上计算公式的推导过程，还存在着一些问题：①虽然动力学方程可以用达西定律来替代，但浆液的运动是非恒定的，没有考虑连续性方程；②浆液压力使土体孔隙率增大，甚至可能导致地表抬动，公式没有考虑孔隙率随注浆压力变化的影响；③公式还远未成熟，实用价值有限。尤其是宾汉浆液柱形公式存在较多参数，计算结果很不稳定。因此，本文从连续性方程出发进一步研究浆液的扩散半径，并用FLAC软件分析了浆液和地下水的二相渗流过程。

2 柱形扩散半径的进一步探讨

传统经典渗透公式的推导，仅使用了达西定律作为动力学方程，但速度分量仍要满足连续性方程。因此，下面从连续性方程出发，考虑浆液压力对土体孔隙率的影响，对浆液在多孔介质中的渗流规律做进一步的研究。

在实际的注浆工程中，浆液从注浆管中流出来后再向上返，直至充满整个灌浆孔段，非常符合线性源理论[2]，可以归结为平面流动问题。因此，大多数注浆都使用柱形扩散模型，如图1所示。图中注浆压力pr假设为常数，l为注浆段的长度。

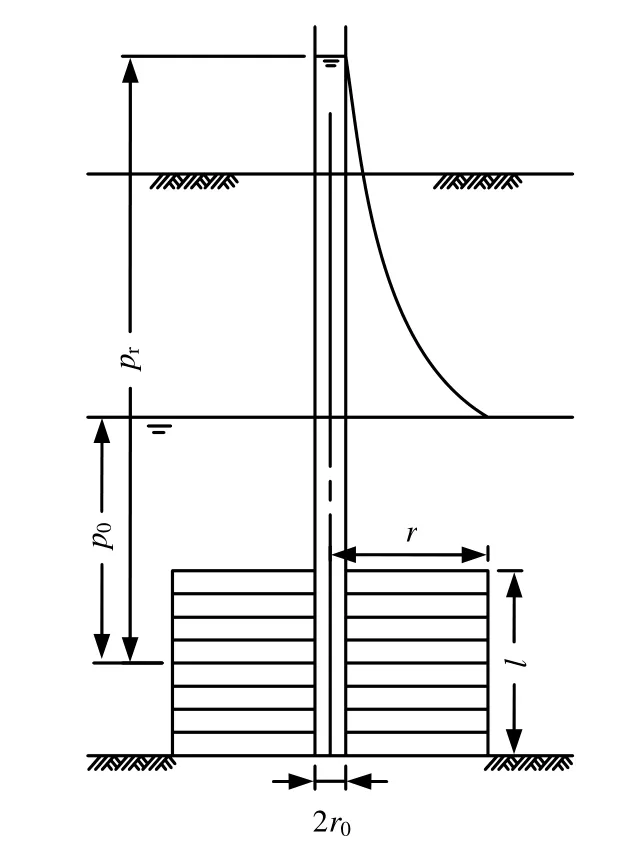
图1 浆液柱形扩散的渗透模型Fig.1 Column flow model of grout diffusion

一般情况下，把浆液在介质中的流动作为层流考虑，而浆液在地层中的流动和地下水的流动规律非常相似，因此，仍然可以借用地下水的流动规律来近似考虑浆液的流动。设浆液流速为v，压力为p，有

式中：Kg、Kw分别为浆液和水在土体中的渗透系数；h为浆液的压力水头；γw为水的重度。

当考虑到多孔介质的孔隙率n后，一维状态下连续性方程为[3]

当浆液压力增高时，土的孔隙率要增大，在最简单的情况下有

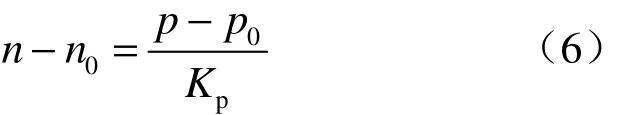
式中：Kp为土的体积变化模量，即产生单位孔隙率变化所需要的压力变化；n0为压力 p=p0时的孔隙率。假定Kp为常数，而浆液的渗透系数k在一定时间范围内不变，则把式（4）、（6）代入式（5）后得

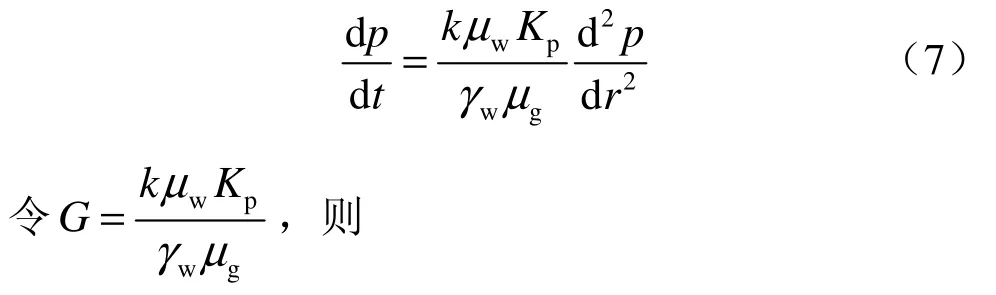
式（8）是一维热传导方程，p可以看作是关于r、t的函数。

初始条件：

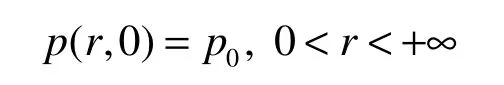
边界条件：

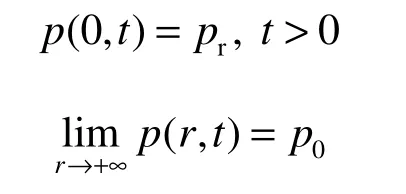
用拉普拉斯变换法求解偏微分方程（7）的初边值问题得

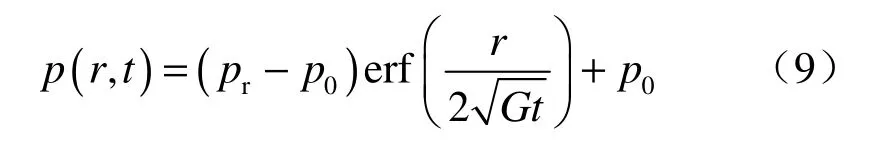
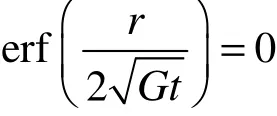
3 注浆过程的二相流模拟

以上介绍的渗透注浆理论，只是对浆液的单一流动形式进行分析，浆液的渗透系数由水的渗透系数除以浆与水的黏度比得到。实际上，当浆液在压力作用下灌入地层时，其渗透过程是地下水和浆液在多孔介质中的两相非稳定渗流。

两相渗流是指多孔介质中存在两种彼此不混溶的流体同时流动，相互作用、相互影响，具有不同于单相流体渗流规律的一种流动形式[4]。它们都沿着自己的网状通道流动，这些通道比单相流动时可能要迂回曲折得多。在通常情况下，孔隙内的被驱替相不可能完全流走，固体表面上总还残留着一层润湿流体。

3.1 水和浆液的二相渗流原理

在两相流中存在3种界面，即流体之间和两种流体与多孔介质表面之间的界面。在界面上由于各相内部的分子间的引力差会产生表面张力，由此引出了固体被液体润湿的概念。对于饱和土体，在灌浆之前孔隙中已充满了地下水，假设浆液和水互不混溶。浆液是以较高的速率被压入到多孔介质中，从中驱替出孔隙水，这个过程是一种非稳定渗流状态。图2为浆液驱水的二相渗流模型。两种流体之间的压力存在不连续性，这个压力差称为毛细压力：

式中：pc为毛细压力；pg为浆液的压力；pw为水的压力。已经可以证明[5]，在低速流的情况下，尤其是在浆液推进的锋面带中，饱和度的梯度比较大，毛细压力就不能忽视。

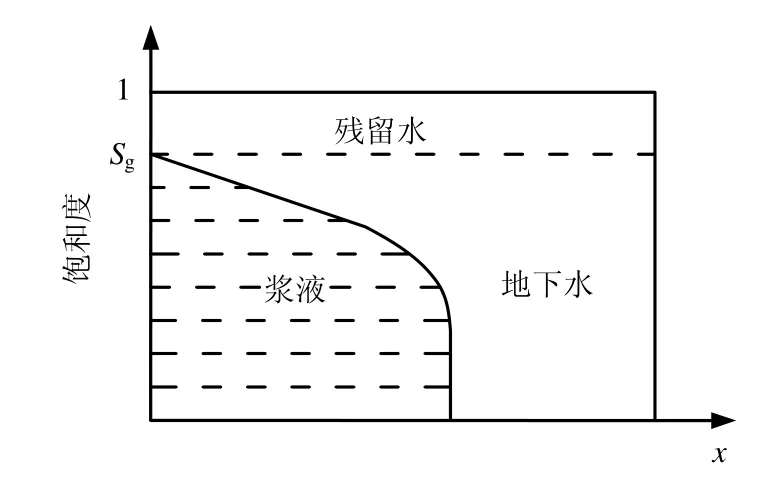
图2 浆液驱水的二相渗流模型Fig.2 Two-phase flow model of grout driving water

每一流体的流动由达西定律表示，当水或浆的饱和度为1时，介质分别相对于水或浆液的渗透率就是介质固有的渗透率。但当二相渗流时，因孔隙中同时存在两种流体的流动，介质渗透率不仅与其孔隙特征有关，同时还与各自的饱和度有关[6]。显然两相流各相渗透率小于介质固有的渗透率，称其为有效渗透率，其值与介质固有渗透率之比称为相对渗透率。

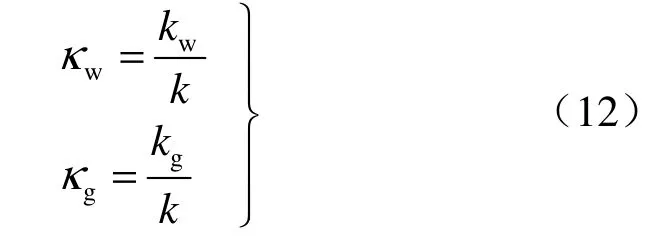
式中：kw、kg为水和浆液的有效渗透率；k为土体介质的固有渗透率；κw、κg分别为水和浆的相对渗透率，仅仅依赖于饱和度的函数。相对渗透率是将单相流体的运动方程推广到两种或两种以上流体同时流动的基础。因此，达西定律可以另写为

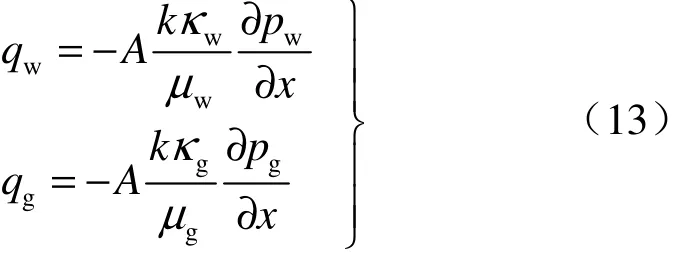
式中：q、p分别代表各相流体的流量、压力；A为过流断面积。

达西定律实质上就是流体流过多孔介质的运动方程。为了求解通过多孔介质的整个流运动问题，还必须结合连续方程[7]：

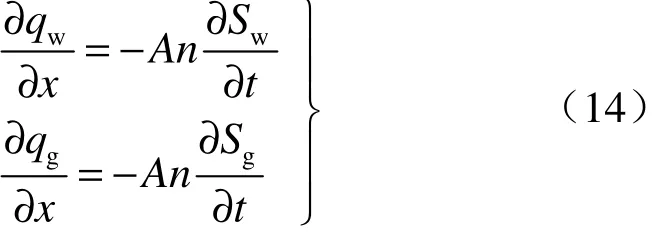
式中：Sw为水的饱和度；Sg为浆液的饱和度。水和浆液完全充满整个空隙，因此有

在某一过水断面上的总流量为

对于不混溶流体，由于毛细作用的结果，流体之间不可能存在宏观意义下的突变界面，即不存在完全把两种流体分隔开的连续界面。它们之间存在一个过渡带，越过此带流体从一种成分变到另一种成分。因此，某点处关于某一流体的饱和度也是变化的。

FLAC中的两相流模块可以进行水下帷幕注浆的数值建模。控制方程就是基于以上表达式，采用有限差分方式求解，另外还要分别获得相对渗透率、毛细压力与饱和度之间的关系，才可求得任一时刻浆液的饱和度分布情况。在FLAC的数值实现中，内置了 Van Genuchten[8]形式的相对渗透率经验法则和毛细管压力曲线。

3.2 工程实例

FLAC中的两相流模块可以进行两种不混溶流体通过孔隙介质而流动的数值模拟[9－10]。孔隙由水和浆液完全充填，其中地下水比水泥浆更能浸润孔隙介质。浆液在压力作用下驱动地下水流动，但它们之间不发生质量转移。控制方程就是基于以上表达式，采用有限差分方式求解，同时两相流还可以与固体进行耦合分析。下面以某土石坝为例，利用FLAC中的二相流模块对注浆过程进行模拟分析。

某大坝为均质土坝，坝顶长为 500 m，宽为7.5 m，最大坝高为58.5 m。坝体填土多为粉质黏土，下部夹有碎石，厚40～50 m，填筑质量较差。坝基为风化砂岩，较破碎，大坝填筑时清基不彻底。水库建成蓄水后，坝下游出现渗漏，日平均渗漏量约3000 m3。其中K0+250～K0+300段，强风化岩出露于坝基，地层构造复杂，存在F17顺河向断层，是大坝渗漏的主要来源。

鉴于前期对坝体进行过劈裂灌浆处理，这次对强风化接触带和坝基采用自上而下分段灌浆法进行防渗加固，灌浆深度从坝顶以下55 m处开始，每5 m一段。为了合理布置帷幕灌浆孔的间距，必须确定浆液扩散的半径，因此，取过坝轴线的纵截面建立二维有限差分模型。本例模拟灌浆段55～60 m的施工，模型从地下水位（深度29 m）开始，到坝深70 m处，地下水位以上采用等效荷载施加于模型表面，共12300个单元，12741个节点。采用水灰比为 1:1的水泥浆施工，浆液与水的黏度比取4.398[11]。模型的上下边界保持孔隙水压力不变，水的饱和度为1。初始状态下孔隙介质完全被水充填。在模拟计算中，岩土本构关系采用摩尔-库仑模型，根据前期的大坝安全鉴定报告和渗漏通道探测报告，各物理参数取值见表1。

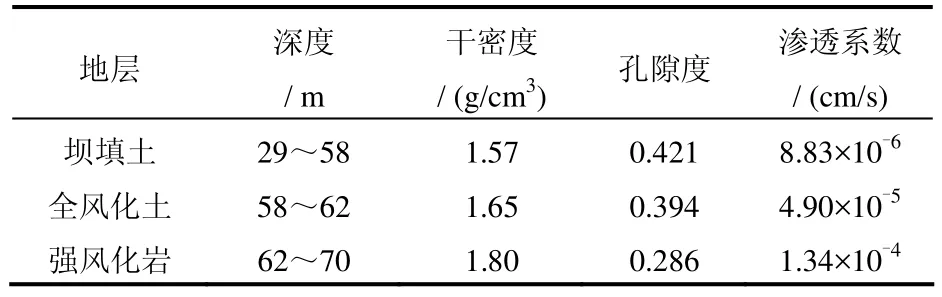
表1 大坝各地层深度及物理参数Table1 Depth and physical parameters of dam strata

图3为灌浆1800、5400、10800 s后Sw分布的等值线图，1-Sw就是浆液的分布。从图中可以看出，浆液呈柱状向外扩散，在靠近注浆段处，浆液的饱和度较大且分布均匀。随着时间的增加，浆液扩散得越远，但扩散的速率逐渐减小。计算结果与实际检测结果吻合，钻孔K0+280在旁边0.6 m处重新钻孔时，发现有水泥和土胶结在一起的混凝土岩芯。分布规律也证明一些渗透注浆理论采用柱形模型是可行的，但在不同地层上浆液的扩散范围是不同的。从图中可以清楚地看到，浆液和水之间的过渡区，取浆液饱和度达到0.9处的扩散距离与柱形公式（2）、本文公式（10）相比较，见图4、5。通过对比可以发现，柱面公式计算出的扩散半径明显偏小，公式（10）和FLAC计算的结果在开始阶段较为接近，但采用二相流理论浆液扩散速率递减地更快。这是因为在浆液前锋处，饱和度的梯度比较明显，毛细压力较大，当浆液不能克服毛细力的作用时，浆液就会停止运动，以往的渗透注浆理论均反映不出这一点。另外，扩散半径不仅与渗透系数有关，还与孔隙度有关，而且孔隙度较渗透系数对扩散半径有着更大的影响。

图6为在扩散半径0.2 m处竖直两点（0.2,11）、（0.2,13.4）浆液流速的变化。点（0.2,11）处是全风化土，点（0.2,13.4）是坝填土。由于填土的孔隙度比全风化土要大，在初始阶段，填土中的孔隙很快便充满浆液，速度比全风化土要快，但填土的渗透系数较小，接下来全风化土中的浆液的流量超过了上层填土，扩散得更快，但由于孔隙度小，很难再继续向前流动了；再结合图3(c)，坝填土的渗透系数虽然较下层偏小，但其孔隙度大，反而扩散得更远。

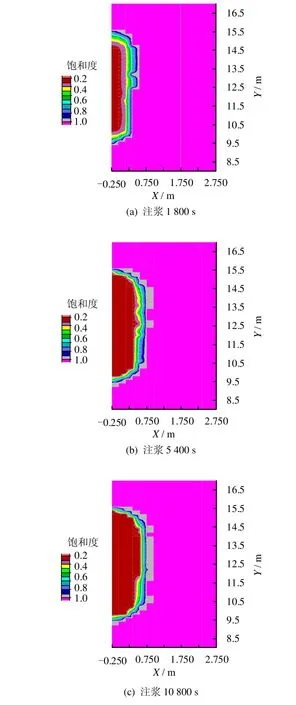
图3 注浆后不同时刻水的饱和度分布Fig.3 Water saturation degrees of different times after grouting

图4 坝填土中浆液扩散半径对比Fig.4 Comparison of grout diffusion radius in dam fill

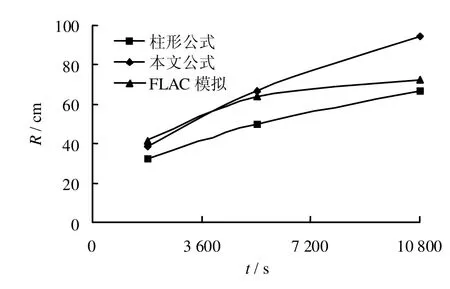
图5 全风化土中浆液扩散半径对比Fig.5 Comparison of grout diffusion radius in weathered soil

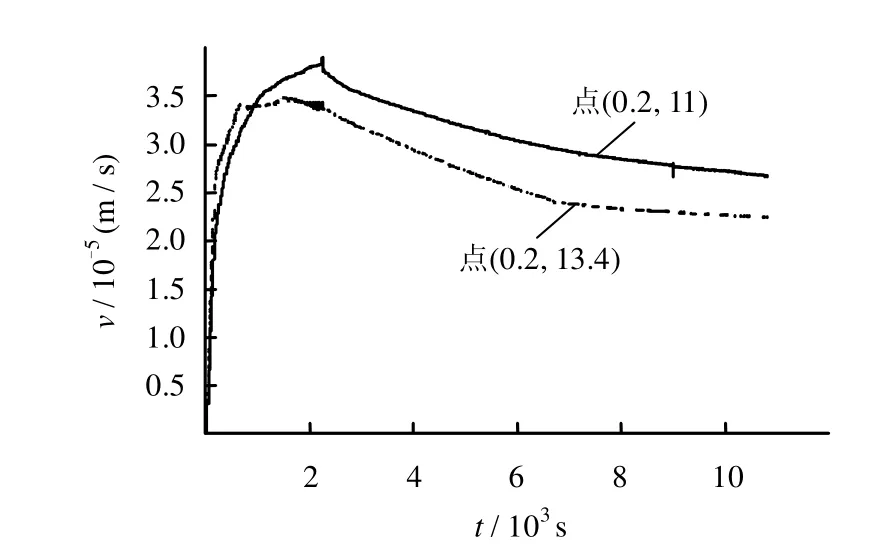
图6 点(0.2,11.0)、(0.2,13.4)处的浆液流速变化Fig.6 Variation of grout flow at points(0.2,11.0) and (0.2,13.4)

图7为注浆段中间水平两点（0.2，12.4）、（0.4，12.4）浆液流速的变化。由于点（0.2，12.4）非常靠近注浆孔，浆液流量在开始时出现了较大的升高；当浆液扩散到点（0.4，12.4）时，流量逐渐增加，最后与点（0.2，12.4）保持一致。在浆液开始流动时，渗透速度不断增大，这是因为在开始阶段土体的孔隙是联通尚未被浆液填塞的，浆液在土层中的渗透系数较大。之后先流入的浆液将土体中的孔隙通道堵塞，使压力损失变大，渗透速度趋于稳定并有减小的趋势。

图7 点(0.2,12.4)、(0.4,12.4)处的浆液流速变化Fig.7 Variation of grout flow at points(0.2,12.4) and (0.4,12.4)

4 结 论

（1）本文推导公式在开始阶段与二相流模拟的结果相近，到了后期FLAC计算的浆液运动的速率比较慢。由此可见，在浆液的前锋处，毛细压力的作用不可忽略。

（2）FLAC二相流模拟结果表明：浆液和水之间存在着一个过渡带，浆液的饱和度在不同时间和位置上是变化的；扩散半径不仅与渗透系数有关，还与孔隙度有关，而且孔隙度较渗透系数对扩散半径有着更大的影响。

（3）二相流模拟有其独特之处，可以较好地模拟注浆的施工过程，分析浆液的扩散距离，并为实际生产提供参考和指导。

[1]岩土注浆理论与工程实例协作组. 岩土注浆理论与工程实例[M]. 北京: 科学出版社,2001.

[2]何修仁. 注浆加固与堵水[M]. 沈阳: 东北工学院出版社,1990.

[3]BEAR J. Hydraulics of groundwater[M]. New York:McGraw-Hill,1979.

[4]张良辉,熊厚金,张清. 浆液的非稳定渗流过程分析[J].岩石力学与工程学报,1997,16(6): 564－570.ZHANG Liang-hui,XIONG Hou-jin,ZHANG Qing.Analyses of the unsteady permeation process of grout[J].Chinese Journal of Rock Mechanics and Engineering,1997,16(6): 564－570.

[5]贝尔 J. 多孔介质流体动力学[M]. 李竞生,陈崇希译.北京: 中国建筑工业出版社,1983.

[6]DULLIEN F A L. 多孔介质——流体渗移与孔隙结构[M].杨富民,黎用启译. 北京: 石油工业出版社,1990.

[7]薛定谔 A E. 多孔介质中的渗流物理[M]. 王鸿勋,张朝琛,孙书琛译. 北京: 石油工业出版社,1982.

[8]VAN GENUCHTEN M TH. A closed-form equation for predicting the hydraulic conductivity of unsaturated soils[J]. Soil Science Society of America Journal,1998,44: 892－898.

[9]刘波,韩彦辉. FLAC原理、实例与应用指南[M]. 北京:人民交通出版社,2005.

[10]Itasca Consultiong Group Inc. FLAC user′s manuals,version 5.0[M]. Minneapolis: Itasca Consultiong Group Inc.,2005.

[11]刘文永,王新刚,冯春喜,等. 注浆材料与施工工艺[M].北京: 中国建材工业出版社,2008.