岩石矿物细胞元随机性参数赋值方法研究

罗 荣，曾亚武

（武汉大学 土木建筑工程学院，武汉 430072）

1 引 言

岩石是经过多种地质作用形成的天然矿物集合体，在漫长的地质年代经历了结晶过程的演化、高温、高压的影响以及各种地质营力的作用，形成了极其复杂的结构和构造特性，其中最基本的特性之一就是岩石的非均质性[1]，即岩石是由不同的矿物颗粒集合体和胶结材料组成的非均质体。大多数岩石是由几种矿物组成的，岩石中的矿物成分及其含量，是决定岩石物理力学性质的主要因素，在某些条件下甚至会产生决定性影响[2]。

对于岩石类非均质材料，在外力作用或环境因素（如温度）改变等条件下，材料内部的应力和变形分布是相当复杂的，主要表现就是其物理力学性质的高度非均匀性和非线性，而微观介质（可以理解为矿物颗粒）参数的不均匀性是造成岩石力学性质非均匀和非线性的主要原因[3－4]。大量的岩石力学试验结果也表明岩石试样的物理力学性质参数存在较大的离散性，这种试验结果的离散性并不完全是由试验条件等外部因素引起的，岩石自身的非均质性是一个重要的影响因素[5]。岩石的非均质性主要是由构成岩石的矿物颗粒的物理力学性质的差异性决定的，矿物颗粒的力学性质差异越小岩石均质性越好；反之则岩石均质性越差。岩石力学的分析方法要成功地解决实际岩土工程中的问题，必须考虑岩石的非均质特性[6]。

事实上，国内外学者已经在如何考虑岩石的非均质特性方面开展了一系列工作，并取得了大量的研究成果。Song和 Kim[7]，Napier和 Dede[8]，Li等[9]应用格构模型分析了原岩的破坏过程，岩石材料的非均质性通过随机指定格构单元的强度和形状实现；唐春安[3,10－11]和 Kaiser[10－11]利用 Weibull分布函数描述岩石材料的非均质参数，对二维问题做了较详细地研究；陈永强等[12]对三维非均质脆性材料的破坏进行了研究和数值模拟；王学滨[13]对含初始随机材料缺陷的岩样破坏受峰后脆性的影响进行了数值模拟；康健等[14－15]利用随机分布参数研究了岩石热破裂现象；许湘华等[16]在进行边坡可靠度分析时利用节理面的随机分布考虑了节理几何参数的不确定性。总体来说，上述研究中对岩石非均质特性的处理方法主要为对网格模型中的各单元体赋予不同的参数。因为岩石力学参数是岩石工程设计分析的关键性参数，其取值决定了计算结果的准确性、客观性和实用性，因此，准确地反映岩石的力学参数以及不均匀的分布规律，对于岩土工程设计、施工和分析评价都具有重要的意义[17]。因此，研究岩石非均质性从微观参数的不均匀分布着手，研究方向无疑是正确的。但上述研究中，对材料非均质性的处理采用了统计分析加随机赋值的方法，即先按一定的网格尺寸将材料作网格划分，假定网格单元的材料力学参数服从某一统计分布规律（如正态分布或Weibull分布等），然后再由确定的分布规律产生一个离散的材料力学参数值序列，并按 Monte Carlo随机方法投放到各网格单元中去。这类方法对网格单元力学参数的赋值是随机的，没有考虑岩石的结构和构造特征。

从力学角度来看，岩石的非均质性还表现为力学参数的空间变异性，这种变异并不是完全随机的，而是具有随机性和结构性的二重性。张征[18]、谭文辉[19]、胡小荣[20]等基于地质统计学方法的区域化变量理论，考虑岩体力学参数的空间变异二重性特征研究了岩石的非均质赋值方法，该种分析处理并不采用传统的概率统计方法，而是通过对样品数据进行结构分析并借助变异函数这一工具来反映参数变量所具有的二重性特征，但这种方法由于本身存在的整体相关性和平滑化效应问题，单元赋值的精度不高，还有待进一步研究[20－21]。

由此可知，在考虑岩石的非均质性时，除了考虑微观力学参数的随机性外，更重要的是必须考虑岩石组成种类及含量所产生的结构性。本文提出了一种新的描述岩石非均质特性的有限元参数赋值方法——岩石矿物细胞元随机性参数赋值方法，即将每一个有限元网格视为一个组成岩石矿物细胞元，基于组成岩石的矿物种类和含量，定义单元类别判定区间，对各个矿物细胞元进行矿物类别判定，并进行参数赋值，完成赋值过程。该方法通过组成岩石的矿物种类和含量，描述岩石非均质参数的结构性；不同种类的矿物颗粒集合体在岩石中的分布是随机的，也不失随机性。

2 岩石矿物细胞元随机性参数赋值方法

假定组成岩石的矿物颗粒在局部范围内具有相同的物理力学性质，这样根据有限元计算要求剖分所得的网格单元，都可以代表一个局部范围的矿物颗粒，并将其称之为矿物细胞元[4]，具有相应的物理力学性质。岩石矿物细胞元随机性参数赋值方法就是要判定每一个矿物细胞元的矿物属性，同一类别的矿物细胞元赋予相同的物理力学参数，其参数赋值流程如图1所示，步骤如下：

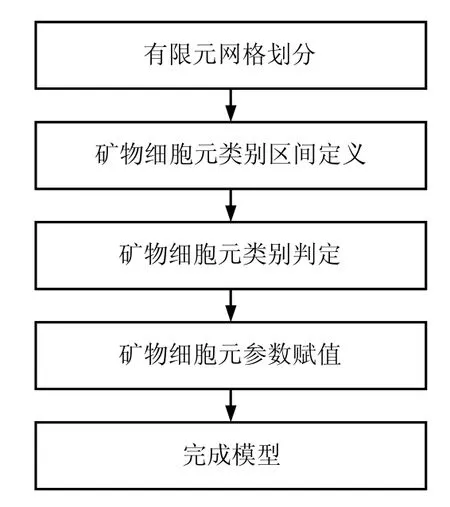
图1 矿物细胞元随机性参数赋值流程图Fig.1 Flow chart of random parameter assignment of rock mineral cell unit

（1）根据研究对象尺度确定合适的有限元网格剖分尺寸，并进行有限元网格剖分。如对于岩石材料类问题，可以考虑细观尺度的有限元网格剖分；

（2）根据岩石的矿物含量或工程问题的非均质特征定义矿物细胞元类别判定区间；

（3）利用Monte Carlo方法确定的一组离散的随机数，逐个进行矿物细胞元类别判定；

（4）根据各矿物细胞元类别属性，赋予相应的物理力学参数。

通过上述过程，即可建立起描述岩石非均质性的有限元模型。

2.1 矿物细胞元类别区间定义

图2 岩石矿物含量示意图Fig.2 Contents of the rock minerals

令

定义区间 Ai=[ui-1,ui)（其中i=1，2，…m-1；当i=m，取右闭区间）为岩石矿物细胞元类别判定区间，即将[0，1]区间划分为m个区间，区间 Ai即为第i类别矿物的细胞元判定区间。由于区间 Ai在[0，1]区间所占比例为 ui-ui-1=ni，ni又为矿物 i的实际含量，所以判定区间 Ai与矿物i的含量有一一对应关系。

2.2 矿物细胞元类别判定

利用Monte Carlo方法，产生一组随机数序列，该系列随机数的个数与矿物细胞元数相同。依次利用该组随机数序列，根据定义的矿物细胞元类别判定区间对细胞元进行类别判定。

2.2.1 Monte Carlo方法

Monte Carlo方法的理论依据是概率论中的大数定理，是一种通过随机变量的数字模拟和统计分析求取数学物理工程技术问题近似解的数值方法。其基本思想是：首先为所要处理的问题建立一个概率模型，使所求问题的解刚好是该模型的参数、特征量或相关量；然后，通过统计试验产生该问题的统计抽样样本；最后分析这些样本的特性，并以此作为原问题的近似解。

Monte Carlo方法的主要手段是用随机数进行统计试验，产生符合某种统计规律的随机数是应用Monte Carlo方法的基础。首先产生[0，1]区间均匀分布的随机数，然后利用这些随机数产生服从其他分布的随机数或统计量。设随机变量x服从概率密度函数为f(x)的分布，其概率分布函数为F(x)。

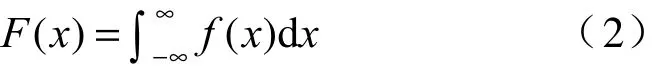
图3、4分别为随机变量x的概率分布函数曲线和概率密度函数曲线示意图。首先产生一组服从[0，1]区间均匀分布的随机数序列ξi，根据累计分布函数式，对于 F(xi)=ξi利用其反函数求出相对应的xi，对于xi，根据概率密度函数可计算 f(xi)。这样，由均匀随机数序列ξi映射为一组特殊序列xi，由大数定理可知，当n取得足够大时，xi服从概率密度为f(x)的分布，即由[0，1]区间的均匀随机数映射得到一组服从给定分布的随机数。

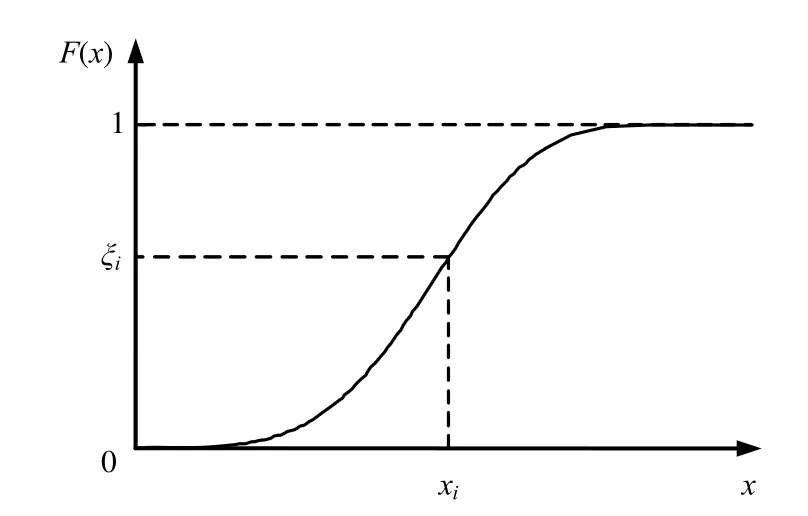
图3 概率分布函数曲线示意图Fig.3 Curve of probability distribution function

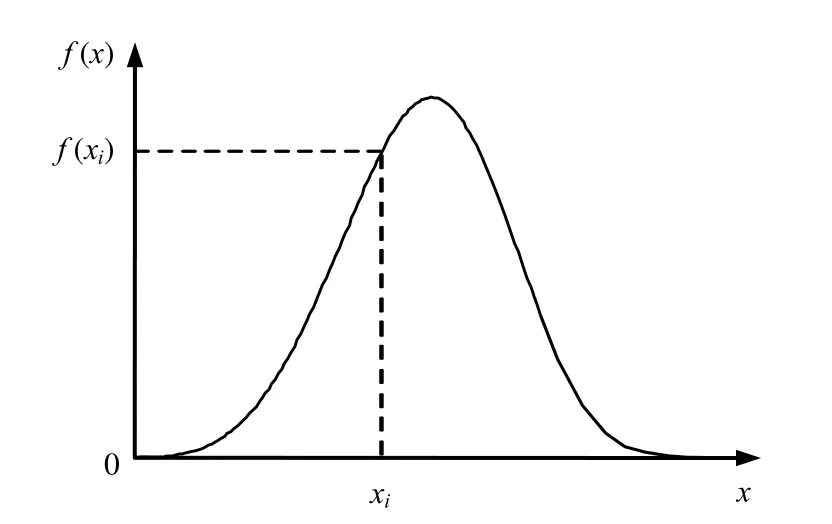
图4 概率密度函数曲线示意图Fig.4 Curve of probability density distribution function

2.2.2 矿物细胞元类别判定

选用[0，1]的均匀分布作为随机序列目标分布，概率分布函数为F(x)=x，概率密度函数为f(x)=1。根据Monte Carlo方法，对于初始随机数ξk，令F(xk)=ξk，即得到用以进行矿物类别判定数序列xk=ξk。

根据定义的细胞元类别判定区间 Ai，依次判别xk的所属区间，如图5所示，若 xk∈Ai，则判定该单元为第i类别矿物细胞元，并对该细胞元赋予相应的i类别物理力学参数。依次对所有的矿物细胞元进行类别判定和赋值，即完成整个模型的赋值。

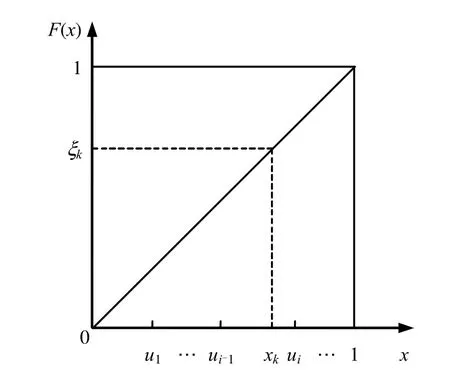
图5 矿物细胞元类别判定示意图Fig.5 Schematic diagram of sort judgment for rock mineral cells

由于矿物细胞元类别判定数xk是服从[0，1]均匀分布的随机数序列，细胞元类别判定为第i类别矿物细胞元的概率 Pi=ui-ui-1=ni，又ni为第 i类别矿物的含量，故细胞元的类别判定概率与矿物的真实类别含量相等。

矿物细胞元混合模型通过真实地反映岩石的矿物含量来描述岩石的非均质性，且模型使各矿物细胞元处于随机均匀混合状态，因此，该模型进行岩石非均质参数赋值时既考虑了岩石参数的结构性特征，又考虑了矿物细胞元的随机分布特征。

3 矿物细胞元分布的随机性特征

本文提出的岩石矿物细胞元随机性参数赋值方法的主要思想是利用组成岩石的矿物种类及其含量定义矿物细胞元类别判定区间。利用Monte Carlo方法，产生服从[0，1]均匀分布的随机数序列作为类别判定数列，利用定义的判定区间依次对细胞元进行类别判定并相应赋值，使各类别矿物细胞元均匀随机混合。

矿物细胞元的类别判定中采用的服从[0，1]均匀分布的随机数序列决定了矿物细胞元分布具有随机性。虽然细胞元的类别判定区间使得各类别细胞元含量在概率上与岩石的矿物含量相等，但对于确定的细胞元类别判定区间，随机数取[0，1]区间任何一个数的概率都相等，因此，服从[0，1]均匀分布的随机数序列不是惟一确定的，判定数序列的随机性引起矿物细胞元的类别判定具有随机性，从而导致矿物细胞元的分布具有随机性特征。

对同一类别矿物细胞元组成的岩石有限元模型，仅有[0，1]一个细胞元类别判定区间，对任意服从[0，1]均匀分布的随机数序列，所有的矿物细胞元都能被惟一地确定为同一类别，即等同为均质模型，所有的矿物细胞元具有相同的物理力学参数，此时矿物细胞元的分布不具有随机性特征。

对由多种矿物细胞元组成的岩石有限元模型，各单元依次进行矿物细胞元类别判定并对不同类别的矿物细胞元赋予不同的参数值，此时，类别判定数序列作为矿物细胞元类别判定指标具有的随机性特征将直接影响类别判定结果，使得描述岩石非均质性的有限元模型不具有惟一确定性，依赖于随机数序列具有随机性特征。如图6、7分别为两矿物细胞元赋值混合模型和三矿物细胞元赋值混合模型示意图，相同的岩石矿物含量定义相同的判定区间，但不同的随机数序列进行矿物细胞元类别判定后获得的岩石非均质模型具有明显的随机性特征。

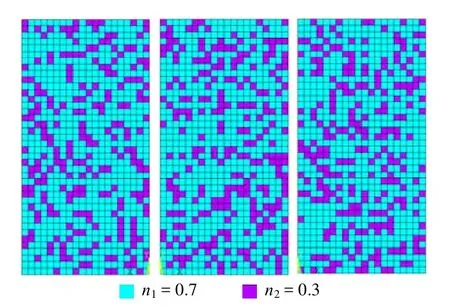
图6 两矿物细胞元赋值Fig.6 Assignment of two mineral cell units

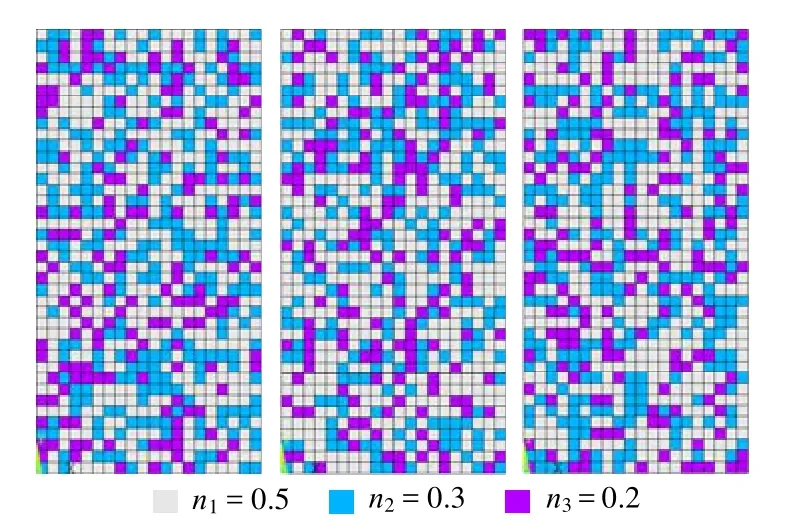
图7 三矿物细胞元赋值Fig.7 Assignment of three mineral cell units

4 岩石矿物细胞元随机性参数赋值数值试验

岩石的宏观力学特征是由组成岩石的各类矿物细胞元共同作用的结果[2－3]。为研究岩石矿物细胞元分布的随机性特征对岩石宏观力学特征的影响，本文在弹性范围内，对相同的岩石矿物种类和含量，利用不同的随机数序列进行矿物细胞元类别判定并赋值后建立的有限元模型进行了数值试验研究。

4.1 数值试验模型

为简化计算，在进行有限元数值试验时，采用线弹性本构关系。考虑岩石由两矿物组成或三矿物组成，各选择6组不同物理参数或矿物含量的试件，对每组试件进行10次矿物细胞元类别判定，建立矿物细胞元混合模型，用以研究矿物细胞元分布的随机性特征对岩石宏观弹性模量的影响。

数值试验采用平面应变模型，试件几何尺寸为20 cm×10 cm，有限元单元（即岩石矿物细胞元）尺寸为0.5 mm×0.5 mm[4]，共划分400×200个单元，数值试验采用位移加载模式。由于各类岩石材料的泊松比一般为0.3左右，差异性不大，故不考虑泊松比的差异性，计算泊松比取v=0.3；岩石材料弹性模量为1～100 GPa不等，故数值试验中，力学参数仅考虑弹性模量的差异性。对于两矿物和三矿物混合模型，各组试件矿物细胞元弹性模量赋值参数E及矿物含量n取值分别见表1、2。

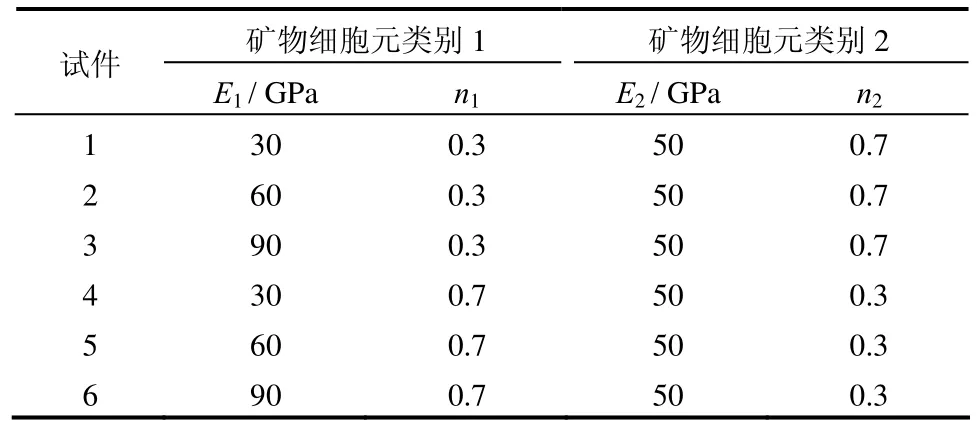
表1 两矿物混合模型数值计算参数Table1 Parameters of two mineral cell units

4.2 数值试验结果分析

对每一组试件，仅考虑矿物细胞元类别判定的随机性影响，进行10次随机类别判定及赋值，分别计算得到的等效宏观弹性模量，如图 8、9及表 3所示。

图9 三矿物混合模型随机性试验结果图Fig.9 Experimental results of random characteristic(three mineral cell units)

表3 两矿物、三矿物混合模型等效弹性模量计算结果Table3 Statistical results of equivalent elastic modulus of two mineral cell units and three mineral cell units

结果表明：

（1）无论是两矿物或三矿物组成的岩石试件，其等效宏观弹性模量计算结果几乎不受矿物细胞元随机分布的影响。

（2）只要矿物种类和含量确定，建立的矿物细胞元混合模型的等效宏观力学参数都非常稳定，各组试件数值试验结果的标准差、变异系数和极差都非常小。

（3）不同类别矿物细胞元之间的弹性模量相差越小，矿物细胞元混合模型的等效宏观弹性模量的标准差、变异系数和极差也越小。

（4）相同矿物含量的岩石矿物细胞元混合模型的等效宏观弹性模量均值随矿物细胞元弹性模量的提高而提高，说明岩石材料宏观力学参数受矿物细胞元力学参数的影响。

4.3 数值试验结果比较

本文采用文献[4]所述的岩石非均质参数赋值方法，对岩石单元的弹性模量进行赋值，进行相关数值试验，计算该方法等效宏观弹性模量的稳定性，单元弹性模量的Weibull分布密度函数表达式为

式中：β为非均质参数；E0为所有细胞元的弹性模量平均值；φ为弹性模量的密度函数值。

为便于比较，E0取岩石矿物细胞元随机性参数方法中两矿物混合模型第1组试件的所有细胞元弹性模量平均值，即取E0=44 GPa；非均质参数β分别取3、6、9、12、15、18。计算结果见表4。

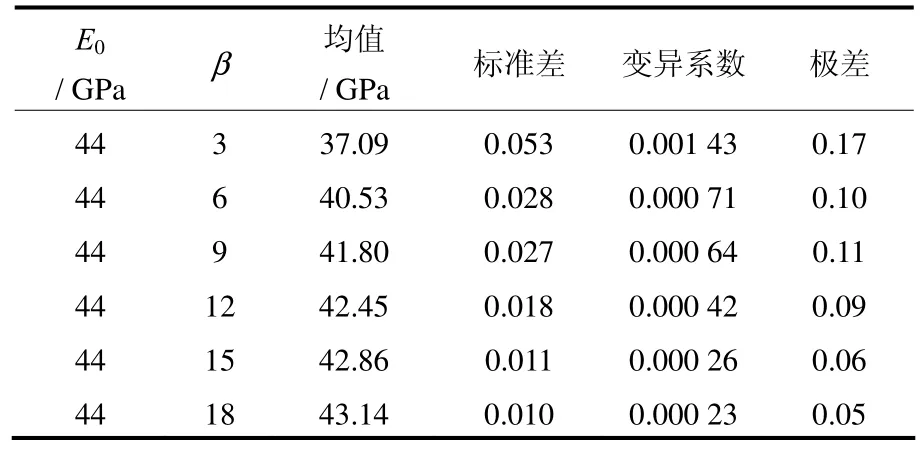
表4 Weibull分布非均质模型等效弹性模量计算结果Table4 Statistical results of equivalent elastic modulus of inhomogeneity model(Weibull distribution)

通过比较可知，采用本文方法计算所得非均质岩石的等效宏观弹性模量值与利用 Weibull分布函数赋值方法（给定非均质参数β）的计算结果在精度和稳定性方面基本一致，说明采用本文方法描述岩石力学参数的非均匀分布是可以接受的。

但与 Weibull分布函数赋值方法相比，本文方法具有以下两个明显特征：

（1）考虑了岩石组成的结构特征，即矿物组成及其含量。只要岩石的矿物组成及其含量确定，就不需要其他的非均质参数即可获得非均质岩石模型，从而避免了非均质参数的选择对岩石力学性能造成的影响。

（2）本文方法可完全退化为均质模型，即该方法可同时用于非均质岩石和均质岩石的数值模拟。

5 结 论

（1）岩石矿物细胞元随机性参数赋值方法考虑了岩石组成的结构特征，在赋值过程中引入岩石自身的矿物种类及含量建立判定函数，在不失随机性的基础上考虑了岩石参数赋值的结构性。

（2）采用简单的[0，1]均匀分布随机数来描述岩石矿物细胞元的随机分布特点，不依赖于其他的随机性参数，避免了采用随机分布（如正态分布，Weibull分布等）时分布参数的选择带来的不确定性影响。

（3）利用Monte Carlo方法进行矿物细胞元类别判定，对单一种类的矿物细胞元构成的模型等同于均质模型，无随机性特征；而对于多种矿物细胞元构成的混合模型，矿物细胞元的随机分布对岩石宏观力学参数的影响非常小，这与利用 Weibull分布函数进行参数赋值得出的结论一致。并且本文方法统一了均质岩石和非均质岩石的数值分析赋值过程，比传统的采用随机分布函数对岩石有限元单元参数进行赋值的方法具有优越性。

（4）组成岩石的各类矿物细胞元力学参数差别越小，岩石越均匀，宏观力学参数的变异性也越小，与利用 Weibull分布函数进行参数赋值得出的结论一致，但本文方法具有自身鲜明的特点。

（5）岩石等效宏观弹性模量随矿物细胞元弹性模量的提高而提高，反映了矿物类型和含量对岩石力学性质的结构性影响。

本文通过数值试验主要研究了岩石矿物细胞元随机分布对岩石宏观弹性模量的影响，至于岩石宏观应力-应变关系、强度及变形特征、裂纹扩展等与矿物细胞元参数及矿物细胞元分布之间的关系还有待进一步研究。

[1]唐春安. 岩石破裂过程数值试验[M]. 北京: 科学出版社,2003.

[2]陶振宇,潘别桐. 岩石力学原理与方法[M]. 武汉: 中国地质大学出版社,1991.

[3]唐春安. 岩石声发射规律数值模拟初探[J]. 岩石力学与工程学报,1997,16(4): 368－374.TANG Chun-an. Numerical simulation of AE in rock failure[J]. Chinese Journal of Rock Mechanics and Engineering,1997,16(4): 368－374.

[4]冯增朝,赵阳升,段康廉. 岩石的细胞元特性及其非均质分布对岩石全曲线性态的影响[J]. 岩石力学与工程学报,2004,23(11): 1819－1823.FENG Zeng-chao,ZHAO Yang-sheng,DUAN Kang-lian.Influence of rock cell characteristics and rock inhomogeneity parameter on complete curve of stressstrain[J]. Chinese Journal of Rock Mechanics and Engineering,2004,23(11): 1819－1823.

[5]张占荣,盛谦,杨艳霜,等. 基于现场试验的岩体变形模量尺寸效应研究[J]. 岩土力学,2010,31(9): 2875－2881.ZHANG Zhan-rong,SHENG Qian,YANG Yan-shuang,et al.Study of size effect of rock mass deformation modulus based on in-situ test[J]. Rock and Soil Mechanics,2010,31(9): 2875－2881.

[6]张渊,赵阳升. 岩石非均质度与热破裂的相关性分析[J].兰州理工大学学报,2009,35(6): 135－137.ZHANG Yuan,ZHAO Yang-sheng. Analysis of correlation of rock thermal cracking with inhomogeneity[J]. Journal of Lanzhou University of Technology,2009,35(6): 135－137.

[7]SONG J,KIM K. Micromechanical modeling of the dynamic fracture process during rock blasting[J].International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts,1996,33(4): 387－394.

[8]NAPIER J A L,DEDE T. A comparison between random mesh schemes and explicit growth rules for rock fracture simulation[J]. International Journal of Rock Mechanics and Mining Sciences,1997,34(3－4): 217.

[9]LI L H,BAI Y L,XIA M F,et al. Damage localizations as a possible precursor of earthquake rupture[J]. Pure and Applied Geophysics,2000,157: 1929－1943.

[10]TANG Chun-an,KAISER K P. Numerical simulation of cumulative damage and seismic energy release during brittle rock failure-Part I: Fundamentals[J]. International Journal of Rock Mechanics and Mining Sciences,1998,35(2): 113－121.

[11]KAISER K P,TANG Chun-an. Numerical simulation of damage accumulation and seismic energy release during brittle rock failure-Part II: Rib pillar collapse[J].International Journal of Rock Mechanics and Mining Sciences,1998,35(2): 123－134.

[12]陈永强,郑小平,姚振汉. 三维非均匀脆性材料破坏过程的数值模拟[J]. 力学学报,2002,34(3): 351－361.CHEN Yong-qiang,ZHENG Xiao-ping,YAO Zhen-han.Numerical simulation of failure processes in 3-D heterogeneous brittle material[J]. Acta Mechanica Sinica,2002,34(3): 351－361.

[13]王学滨. 峰后脆性对非均质岩石试样破坏及全部变形的影响[J]. 中南大学学报(自然科学版),2008,39(5):2394－2399.WANG Xue-bin. Effects of post-peak brittleness on failure and overall deformational characteristics of rock specimen with random material imperfections[J]. Journal of Central South University(Science and Technology),2008,39(5): 2394－2399.

[14]康健,赵阳升,赵峥嵘,等. 随机介质热弹性平面轴对称问题的解析解[J]. 岩土力学,2006,27(10): 1689－1692.KANG Jian,ZHAO Yang-sheng,ZHAO Zheng-rong,et al.Analytical solutions to thermoelastic plane axisymmetric problems for random non-homogeneous media[J]. Rock and Soil Mechanics,2006,27(10): 1689－1692

[15]康健,毕秀国,刘超. 非均质随机分布对岩石热破裂影响的数值试验[J]. 岩土力学,2008,29(增刊1): 491－494.KANG Jian,BI Xiu-guo,LIU Chao. Numerical tests of influence of heterogeneous random distribution on thermal cracking of rock[J]. Rock and Soil Mechanics,2008,29(Supp.1): 491－494.

[16]许湘华,曲广琇,方理刚. 基于节理几何参数不确定性的边坡可靠度分析[J]. 中南大学学报(自然科学版),2010,41(3): 1133－1139.XU Xiang-hua,QU Guang-xiu,FANG Li-gang.Reliability analysis of rock slope based on uncertainty of joint geometric parameters[J]. Journal of Central South University(Science and Technology),2010,41(3): 1133－1139.

[17]李世海,董大鹏,燕琳. 含节理岩块单轴受压试验三维离散元数值模拟[J]. 岩土力学,2003,24(4): 648－652.LI Shi-hai,DONG Da-peng,YAN Lin. 3D-DEM numerical simulation for jointed reck under uniaxial press loading[J]. Rock and Soil Mechanics,2003,24(4): 648－652.

[18]张征,刘淑春,鞠硕华. 岩土参数空间变异性分析原理与最优估计模型[J]. 岩土工程学报,1996,18(4): 40－47.ZHANG Zheng,LIU Shu-chun,JU Shuo-hua. The optimum estimation model and the principle of spatial variability analysis of rock and soil parameters[J].Chinese Journal of Geotechnical Engineering,1996,18(4): 40－47.

[19]谭文辉,王家臣,周汝弟. 岩体强度参数空间变异性分析[J]. 岩石力学与工程学报,1999,18(5): 497－502.TAN Wen-hui,WANG Jia-chen,ZHOU Ru-di. Analysis of spatial variability of strength parameter of rock mass[J].Chinese Journal of Rock Mechanics and Engineering,1999,18(5): 497－502.

[20]胡小荣,唐春安. 岩土力学参数随机场的空间变异性分析及单元体力学参数赋值研究[J]. 岩石力学与工程学报,2000,19(1): 59－63.HU Xiao-rong,TANG Chun-an. Spatial variation analysis of the random field of mechanical parameters for rock and soil and the parameter estimation of elements[J]. Chinese Journal of Rock Mechanics and Engineering,2000,19(1): 59－63.

[21]赵红亮,冯夏庭,张东晓,等. 岩土力学参数空间变异性的集合卡尔曼滤波估值[J]. 岩土力学,2007,28(10):2219－2223.ZHAO Hong-liang,FENG Xia-ting,ZHANG Dong-xiao,et al. Spatial variability of geomechanical parameter estimation via ensemble Kalman filter[J]. Rock and Soil Mechanics,2007,28(10): 2219－2223.