考虑应力状态的悬挂式防渗墙-砂砾石地基管涌临界坡降试验研究
2012-11-05罗玉龙詹美礼盛金昌
罗玉龙,吴 强,詹美礼,盛金昌
(河海大学 水利水电学院,南京 210098)
1 引 言
悬挂式防渗墙是一种十分重要的防渗措施,广泛应用于堤防工程及深厚覆盖层上的高土石坝工程中。防渗墙的建设一方面有利于堤坝的整体稳定性,但另一方面也会在防渗墙底部及周围岩土体内产生较大的渗透坡降。众多专家认为,这可能造成防渗墙底部土体发生局部渗透破坏,甚至诱发大坝整体破坏,建议继续加深防渗墙深度以减小渗透坡降,这样不仅加大了施工难度,显著地提高了工程投资,而且由于墙体深度过大,难以保证质量。
众多学者对悬挂式防渗墙的防渗效果及控制管涌等渗透变形发展的效果进行了广泛的研究,如张家发等[1]通过砂槽模型,模拟了细砂地基中渗透变形的发生和扩展过程,表明悬挂式防渗墙对渗透变形的发生条件影响很小,但对渗透变形的扩展及模型破坏的条件影响显著。毛昶熙等[2]开展了有悬挂式防渗墙的砂质堤基水槽模型管涌试验,对不同贯入度悬挂防渗墙防止管涌效果进行了研究,确定了悬挂式防渗墙及其前后水平段的渗流临界坡降,给出了管涌险情是否影响大堤安全的估算公式。李广信等[3]利用有机玻璃模型槽,模拟二元堤基条件及不同防渗墙深度下,堤基内管涌的发生和发展过程,试验表明悬挂式防渗墙对于管涌出砂量有控制作用,且管涌口环形出砂面积与防渗墙深度线性相关;砂土越密实,越不易发生管涌。丁留谦等[4]研究了双层堤基设置悬挂式防渗墙情况下管涌发展并导致溃堤的过程和机理,试验表明悬挂式防渗墙可以有效地提高堤基管涌破坏的水平平均临界渗透坡降,降低管涌的危害程度,使堤基整体抵抗管涌破坏的能力显著提高。周晓杰等[5]模拟了二元堤基在不同防渗墙深度、位置条件下渗透变形的发生、发展过程。王保田等[6]的试验表明,悬挂式防渗墙的临界表观水力梯度随贯入度的增加而有较大的增加。Tanaka 等[7]、Maeda 等[8-9]、Sakai等[10-11]研究了砂基中板墙周围土体的渗透破坏过程,试验发现,随着板墙上下游水头差的增大,下游砂表面开始破坏,上游砂表面开始下沉,当达到临界状态时,板墙底部土体开始发生侵蚀和流动。上述研究成果加深了对含有悬挂式防渗墙的强透水地基渗透破坏机制的认识,但均没有考虑地基所处的三向受压状态的影响。由于悬挂式防渗墙底端一般距地表几十米(堤防工程)甚至是几百米(深厚覆盖层上的高土石坝工程),防渗墙及强透水地基均处于高压力状态,土体内部的孔隙通道被显著压缩,进而限制了大量潜在可动细颗粒在土体中及防渗墙与土体接触面上的运移,与不考虑应力情况比较,会显著地提高管涌的临界渗透坡降(这里定义管涌临界渗透坡降为土体最早出现极少量细颗粒流失现象时对应的渗透坡降)。然而,已有的研究成果均不能完全体现应力状态对悬挂式防渗墙-强透水地基管涌临界坡降及管涌发展过程的影响,可能造成众多不必要的工程浪费。
为了研究悬挂式防渗墙-强透水地基所处的应力状态对其管涌等渗透变形发展过程影响,本次利用自行研制的土与结构物接触剪切渗透仪,对不同应力状态下悬挂式防渗墙-砂砾石地基管涌临界渗透坡降进行了研究。
2 土与结构物接触剪切渗透仪介绍
笔者新研制的土与结构物接触剪切渗透仪如图1所示。该仪器可研究高应力、高渗压条件下土体与结构物接触面的渗流应力耦合机制,包括围压系统、轴向压力系统、渗透压力系统、数据采集系统及土与结构物模型底座等。围压及轴向压力系统模拟土与结构物承受的高应力状态,最高围压、轴向压力分别可达2.0 MPa和4.0 MPa;渗透压力系统模拟接触面承受的高水力梯度的渗流作用,最高水头达200 m,最低水头0~2 m,能够实现高低水头的快速切换;数据采集系统能够实时监测试样沉降、孔隙水压力消散等。土与结构物模型底座由模拟结构物的硬塑板和可拆卸的金属底座组成,金属底座包含有进水口和出水口,如图2所示。

图1 土与结构物接触剪切渗透仪Fig.1 Photograph of soil-structure contact shear permeameter

图2 模型底座Fig.2 Model base
根据研究目的,本试验不施加轴向压力,仅考虑围压对悬挂式防渗墙-砂砾石地基管涌发生临界坡降及管涌发展过程的影响,渗透压力系统采用低水头模式,由变水头水箱提供,试样进出口端设置测压管以便实时监测总水头变化。试验过程:①按照填筑要求制备试样,并饱和试样。②分级缓慢施加围压,并打开排水管固结排水。③分级施加渗透压力,施加完每级水头后,利用滤网收集流出的细砂,待流量稳定后,测定流量,记录时间及流量,计算渗流速度,绘制出砂量-渗透坡降关系,渗流速度-渗透坡降关系曲线。
3 不同应力状态下防渗墙-砂砾石地基管涌试验
试验土料为 Skempton等[12]研究使用的缺乏中间级配的管涌型砂砾石料A,其颗粒级配曲线如图3所示。拟开展无围压、围压0.2、0.4、0.6、0.8 MPa等5组试验,各组试验砂砾料试样的填筑密度严格控制在1.843 g/cm3,孔隙率在0.31~0.33之间,以保证各组试验成果具有可比性。试验中悬挂式防渗墙高度10 cm,厚1 cm,即渗径长21 cm,试样总高度为20 cm,制备的试样见图4(冷冻后拍摄)。
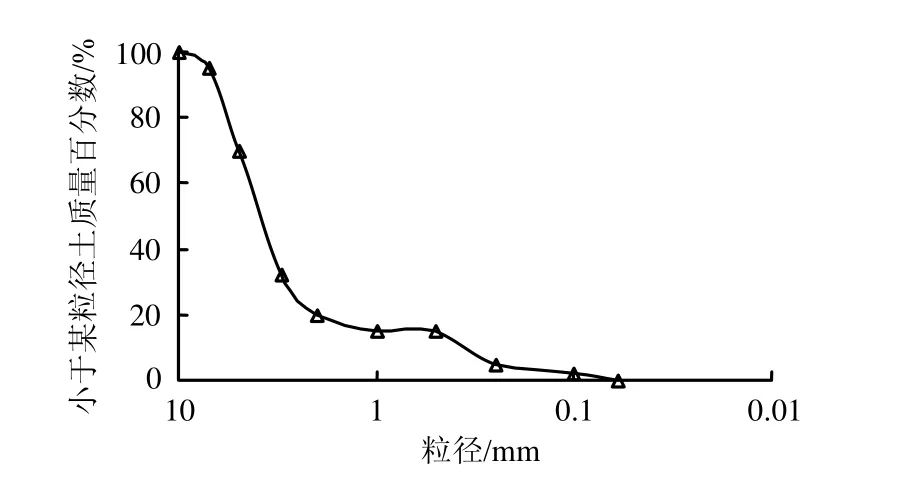
图3 砂砾石颗粒级配曲线Fig.3 Particle size distribution curve of the sand-gravel

图4 悬挂式防渗墙-砂砾石试样Fig.4 Suspended cut-off wall and sand-gravel sample
3.1 无围压试验结果
无围压试验中,渗透坡降i从0.1缓慢增加大2.9(i=进出口两端总水头差/渗径长度)。当i=0.16时,试样开始流出极少量细砂,持续约 3 min,因此,无围压情况下,悬挂式防渗墙-砂砾石地基的管涌临界渗透坡降icr=0.16;此后逐渐抬高水头,均未有任何细砂流出,直到i=0.41时,再次出现极少量细砂流失现象;i在 0.41~1.27之间时,多次出现间断性的极少量细砂流出现象;当i=1.42时,一次出砂量骤然达到0.05 g;此后出现连续性出砂现象,但出砂量极少;当i=2.57时,出砂量骤然加大,达到0.061 g;当i=2.90时,出砂量再次骤然减小。试验结束时,总出砂量为0.4~0.5 g,整个试样未出现明显的管涌破坏现象。
3.2 不同围压试验结果
在围压为0.2 MPa试验中,i从0.18缓慢增加到4.9。试验初期,i在0.18~0.32之间均未见出砂现象;i=0.41时,开始流出2粒细砂,说明icr=0.41;i=0.54时,停止出砂,此后开始出现持续性的出砂,但出砂量极少;当i=1.53时,出砂量骤然增大,达到0.015 g,之后出砂量骤然减小;当i=2.45时,出砂量再次骤然增大,达到0.176 g。此后,随着i的增大,出砂量均较大,其中,i=3.45时,出砂量为0.21 g;i=4.93时,出砂量达到0.32 g。试验结束时,总出砂量达到1.178 g,虽然试验后期持续大量出砂,但试样仍未出现明显的管涌破坏现象,只在出口附近形成了比较明显的大孔隙通道,见图5。从图中可以看出,进水端及出水端都发生了比较明显的细颗粒运移现象。试验结束时,进水端主要剩余大颗粒,与防渗墙的接触面上大颗粒较大。而出水端一方面聚集了从进水端运移过来的大量细颗粒,另一方面,在与防渗墙的接触面上形成了非常明显的大孔隙通道。

图5 围压0.2 MPa时试验结束后试样进出水端Fig.5 The sample inlet and outlet under confining pressure of 0.2 MPa
图6为围压0.2 MPa试验结束后出水端附近颗粒级配曲线与试验前级配的对比。从图中可以看出,试验前后出水端附近区域颗粒级配的最显著区别体现在0.06~0.1 mm的颗粒上,试验结束后,出水端0.06~0.1 mm的颗粒含量已经基本为0,说明试验过程中,所有的0.06~0.1 mm的颗粒已经全部流出试样,这也可以从图5中得到验证。
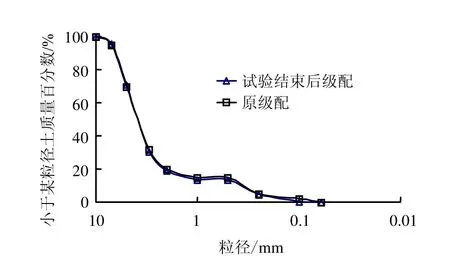
图6 围压0.2 MPa时试验前后出水端土体颗粒级配对比Fig.6 The outlet soil particle size distribution under confining pressure of 0.2 MPa
在围压0.4 MPa试验中,渗透坡降从0.13缓慢增加到5.15,当渗透坡降为0.56时,试样开始出现管涌现象,即 icr=0.56。此后整个试验过程中一直有细砂流出,但出砂量时大时小,其中渗透坡降为0.64~1.84之间时,出砂量极少,而在渗透坡降为2.05、4.22、4.54、5.15时,出砂量分别达到0.054、0.058、0.066、0.103 g,说明管涌的发展过程并不是一直持续的,而是存在细砂侵蚀运移、淤堵于孔隙中、重新冲开孔隙,重新运移等众多复杂现象。试验结束时,总的出砂量达到0.382 g。虽然试验后期也出现持续大量出砂的现象,但试样未发生明显的管涌破坏。在围压0.6、0.8 MPa试验中,icr分别达到0.69、0.84。试验结束时,2个试样均未出现明显的管涌破坏现象。
各试验中监测的渗透坡降i与渗流速度v之间的关系如图7所示。从图中可以看出,随着围压增大,i-v曲线斜率减小,说明试样的渗透系数逐渐减小,尤其是无围压时试样渗透系数远大于其他有围压的试样。此外,i-v关系曲线呈现幂函数特征,不再符合常规的Darcy定律,而是符合毛昶熙等[13]介绍的非Darcy定律。

式中:k为渗透系数;系数m与土体密实度及有效粒径有关。按照上述关系拟合,得到无围压、围压0.2、0.4、0.6、0.8 MPa时i-v经验公式分别为

相关系数均在0.95以上。拟合结果表明,随着围压增大,渗透系数逐渐减小,如图8所示。无围压时渗透系数为 0.113 cm/s,围压 0.8时渗透系数为0.065,仅相当于无围压时的0.5倍。由此可见,应力状态对土体渗透性的影响巨大,图9为不同应力状态下出砂量与渗透坡降的关系。
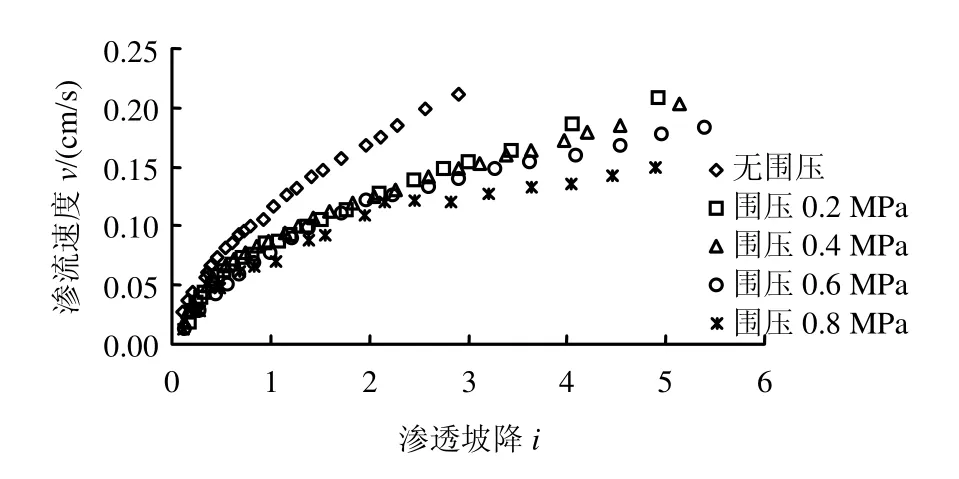
图7 不同应力状态下渗透坡降与渗流速度关系Fig.7 Relationships between hydraulic gradient and flow velocity under different stress states
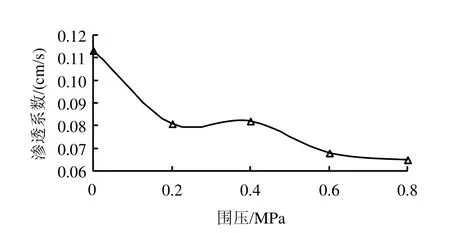
图8 渗透系数与应力状态的关系Fig.8 Relationship between permeability and stress state
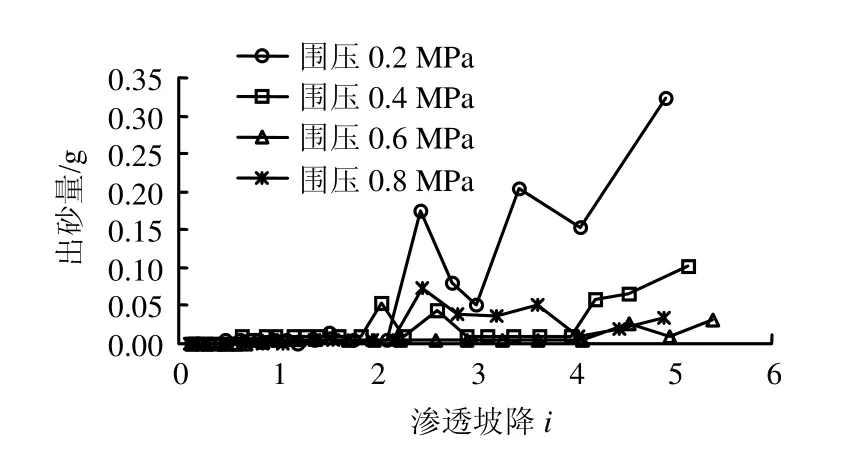
图9 不同应力状态下出砂量与渗透坡降的关系Fig.9 Relationships between eroded sands and seepape hydraulic gradient
从图9可以看出,管涌发展过程中,随着渗透坡降的增大,出砂量并不是一直增大,而出现时大时小的现象,这是因为细颗粒在孔隙通道中运移过程中,当遇到大于其直径的孔隙通道时,细颗粒可以顺利穿过孔隙,而当细颗粒直径大于孔隙时,细颗粒便将堵塞孔隙,导致后面的细颗粒一起停留在堵塞位置,直到继续增大渗透坡降,使得细颗粒冲开堵塞的孔隙时,出砂量才会有显著地增大,但之后孔隙通道可能继续堵塞,导致出砂量的再次降低。即管涌的发展过程就是一个运移-堵塞-堵塞冲开-重新运移的缓慢的、循环往复的过程。
整理不同应力状态下管涌临界渗透坡降发现,其与围压呈现明显的线性关系,如图10所示。按照线性关系拟合,得到不同应力状态下的管涌临界坡降icr经验公式为

相关系数为0.982。
从这一经验公式可以看出,围压越大,防渗墙-砂砾石地基发生管涌的临界渗透坡降就越大,也表明地基越不容易发生渗透破坏。
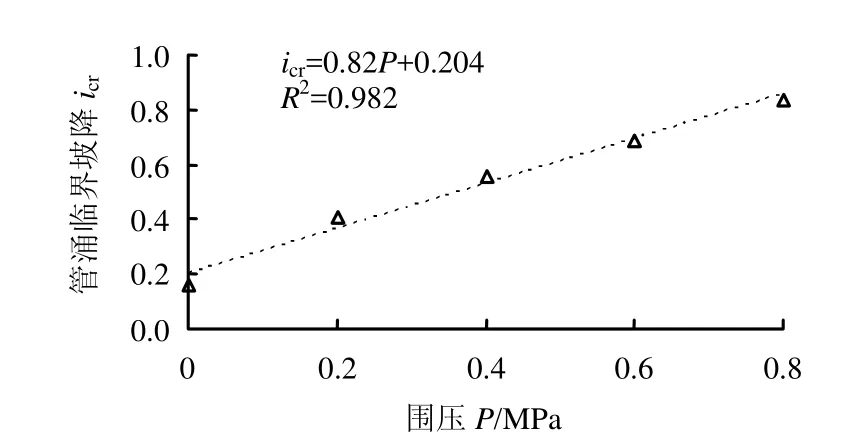
图10 围压与管涌临界渗透坡降关系Fig.10 Relationship between confining pressure and critical piping hydraulic gradient
对于实际工程,只要能够确定悬挂式防渗墙底部所处的应力状态,便可以根据该公式估算其管涌临界渗透坡降,再根据土体的允许渗透坡降(由渗流-应力耦合试验获得),两者对比,综合确定合理的防渗墙贯入深度。
4 结 论
(1)应力状态对悬挂式防渗墙-砂砾石地基的管涌临界渗透坡降影响巨大,围压P与管涌临界渗透坡降 icr之间具有显著的线性关系(见式(3))。该公式可用于确定悬挂式防渗墙在强透水地基中的合理贯入深度,适用于:①围压小于0.8 MPa;②缺乏中间级配的管涌型砂砾石地基。对于我国西南地区众多建设在深厚覆盖层上的200~300 m级高土石坝工程而言,悬挂式防渗墙底部均处于高压力状态,本文的经验公式不再适用,需要开展更高应力状态下的管涌试验研究,但通过本文的研究可以推断,与不考虑应力状态情况相比,高应力状态下悬挂式防渗墙底部附近土体发生管涌的临界渗透坡降必将得到显著提高。
(2)管涌发展过程中,随着渗透坡降的增大,出砂量出现时大时小的现象,这说明管涌的发展过程是一个细颗粒运移-细颗粒堵塞孔隙-堵塞孔隙被冲开-细颗粒重新运移的渐进性恶化破坏过程。
(3)防渗墙-砂砾石系统的渗流流动规律不再符合线性Darcy定律,渗流速度v与渗透坡降i、渗透系数k之间符合v=kim型非Darcy定律。
(4)应力状态对防渗墙-砂砾石系统的渗透性影响巨大,围压越大,渗透系数越小。对于本试验,无围压时渗透系数达到0.113 cm/s,而围压0.8 MPa时的渗透系数骤减为0.065 cm/s。
本文的研究成果体现了渗流-应力耦合效应对防渗墙-砂砾石地基渗透稳定性的影响,提出的管涌临界坡降经验公式将为确定深厚覆盖层中悬挂式防渗墙的合理贯入深度提供重要的理论依据,同时为进一步开展更高应力状态下管涌发展过程的研究提供了有益的借鉴。
[1]张家发,吴昌瑜,朱国胜. 堤基渗透变形扩展过程及悬挂式防渗墙控制作用的试验模拟[J]. 水利学报,2002,33(9): 108-116.ZHANG Jia-fa,WU Chang-yu,ZHU Guo-sheng.Experimental study on seepage deformation propagation control using impervious wall of suspension type[J].Journal of Hydraulic Engineering,2002,33(9): 108-111,116.
[2]毛昶熙,段祥宝,蔡金傍,等. 悬挂式防渗墙控制管涌发展的试验研究[J]. 水利学报,2005,36(1): 42-50.MAO Chang-xi,DUAN Xiang-bao,CAI Jin-bang,et al.Experimental study on piping development control by means of suspended cut-off wall[J]. Journal of Hydraulic Engineering,2005,36(1): 42-50.
[3]李广信,周晓杰. 堤基管涌发生发展过程的试验模拟[J]. 水利水电科技进展,2005,25(6): 21-24.LI Guang-xin,ZHOU Xiao-jie. Laboratory simulation on generation and evolution of piping in embankment foundation[J]. Advances in Science and Technology of Water Resources,2005,25(6): 21-24.
[4]丁留谦,姚秋玲,孙东亚,等. 双层地基中悬挂式防渗墙渗控效果的试验研究[J]. 水利水电技术,2007,38(2):23-26.DING Liu-qian,YAO Qiu-ling,SUN Dong-ya,et al.Experimental studies on the seepage control effects of suspended cutoffs[J]. Water Resources and Hydropower Engineering,2007,38(2): 23-26.
[5]周晓杰,丁留谦,姚秋玲,等. 悬挂式防渗墙控制堤基渗透变形发展模型试验[J]. 水力发电学报,2007,26(2):54-59.ZHOU Xiao-jie,DING Liu-qian,YAO Qiu-ling,et al.Laboratory model test for evolution of seepage deformation controlled by means of suspended cut-off wall in foundation of dike[J]. Journal of Hydroelectric Engineering,2007,26(2): 54-59.
[6]王保田,陈西安. 悬挂式防渗墙防渗效果的模拟试验研究[J]. 岩石力学与工程学报,2008,27(增刊1): 2766-2771.WANG Bao-tian,CHEN Xi-an. Research on effect of suspended cut-off wall with simulation test[J]. Chinese Journal of Rock Mechanics and Engineering,2008,27(Supp. 1): 2766-2771.
[7]TANAKA T,VERRUIJT A. Seepage failure of sand behind sheet piles——The mechanism and praticalapproach to analyze[J]. Soils and Foundations,JSCE,1999,39(3): 27-35.
[8]MAEDA K,SAKAI H,SAKAI M. Development of seepage failure analysis method of ground with smoothed particle hydrodynamics[J]. Structural Engineering/Earthquake Engineering,JSCE,2006,23(2): 307-319.
[9]MAEDA K,SAKAI H. Seepage failure and erosion of ground with air bubble dynamics[C]//Geo-Shanghai International Conference 2010. Shanghai: American Society of Civil Engineers,2010.
[10]SAKAI H,MAEDA K. Seepage and erosion mechanisms of sandy ground due to air bubbles[C]//2008 Fourth International Conference on Scour and Erosion. Kyoto:The Japanese Geotechnical Society,2008.
[11]SAKAI H,MAEDA K,IMASE T. Erosion and seepage failure analysis of ground with evolution of bubbles using SPH[C]//Prediction and Simulation Methods for Geohazard Mitigation. Kyoto: CRC Press,2009.
[12]SKEMPTON A W,BROGAN J M. Experiments on piping in sandy gravels[J]. Geotechnique,1994,44(3):449-460.
[13]毛昶熙. 渗流计算分析与控制(第二版)[M]. 北京: 中国水利水电出版社,2003.
