任意角度水平向荷载下现浇X形桩力学特性研究（II）：截面应力分布

孔纲强，周 航，刘汉龙，丁选明

（1. 河海大学 岩土力学与堤坝工程教育部重点实验室，南京 210098；2. 河海大学 土木与交通学院，南京 210098）

1 引 言

异形截面桩主要通过变化横截面或者纵截面增加单位材料桩-土接触面积，或者改善接触面形式，从而提高桩侧摩阻力。异形截面对提高特定方向水平向承载力也起到了良好的作用，近些年来国内外学者对水平向荷载作用下异形桩承载力特性进行了研究，取得了一些研究成果。

刘云飞等[1]运用数值方法和梯度法，对水平向荷载作用下纵向变截面桩的截面形式设计进行了优化，指出纵向变截面桩可节省混凝土材料约45%。胡培进等[2]针对多级扩径桩的荷载传递规律以及变形特性进行了分析，研究结果表明同等情况下多级扩底桩比常规桩的工程造价可以降低30%～50%。吴泽军等[3]针对纵向变截面桩的水平向承载力特性进行了模型试验研究，测得了水平荷载与侧向位移、桩身应力以及桩顶转角的变化规律，研究结果表明变截面有利于缓解水平荷载下桩-土相互作用的应力集中。石庆瑶等[4]、张永谋等[5]针对空心桩的水平向受力特性进行了研究，并与等条件实心桩进行了对比分析，研究表明空心桩等横截面异形桩可以有效提高横向承载力。詹金林等[6]、贺杰等[7]分别针对壁板桩、Y形桩的水平向承载力特性进行了研究，并取得了一定的成果。袁佶[8]针对现浇 X形桩的水平向受力特性进行了大型模型槽试验和数值模拟研究，分析了现浇X形桩的水平向极限承载力和桩侧土压力分布规律。但上述研究尚未深入开展针对其异形截面在水平向荷载作用下的应力分布以及承载力特性进行研究。

与其他异形桩相似，X形桩具有提高单位体积材料比表面积的特点，但不清楚异形横截面形式是否容易造成水平向荷载作用应力集中现象等情况，因此，如何优化设计异形截面形式，最大限度有效地减小应力集中现象是工程师们需要关注的重要问题之一。

本文利用材料力学知识，基于X形桩任意方向轴惯性矩控制方程和几何截面特性，根据地基反力法的基本原理，分析X形桩在任意水平向荷载作用下截面应力分布规律，及其控制参数变量对截面应力集中现象的影响规律，并在同等情况下，对等周长和等面积的圆形桩、方形桩的力学特性进行对比分析，提出X形截面设计最优化截面设计形式。

2 X形截面应力分布控制方程建立

2.1 控制方程建立

现浇X形桩是利用如字母X形的截面代替传统的圆形截面。现场振动沉管灌注形成的异形横截面灌注桩，其典型的现场现浇X形桩打桩机、X形桩模以及桩周挤土现象如图1所示。

X形横截面形式由外包圆直径 a、开弧间距 b和开弧度θ三个控制变量组成。当θ≥90°时，开弧圆心分别落于X形外直线段延长线交点的内部、角点和外部，并在两相隔交点的对角线及延长线上，如图2所示。图中，点1～3分别表示X截面3个典型的特殊位置。θ取不同值时，X形截面的周长、面积以及轴惯性矩具有相同的表达式。

基于材料力学理论，可以得到X形截面轴惯性矩表达式：

对于任意方向坐标轴ox’的惯性矩可以由旋转公式得到

式中：α为 ox′轴与 ox轴的夹角； IXCCx、IXCCy可以由式（1）求得。

图1 现场现浇X形桩架及桩模实物图Fig.1 Physical diagrams of the XCC pile driver and pile model

图2 现浇X形桩横截面形状示意图Fig.2 Sketch of the XCC pile cross-sectional shape

基于惯性矩公式，对X形桩在任意角度水平向荷载作用下其截面应力的分布规律进行分析。

由材料力学公式可知，水平向荷载作用下X形截面产生的正应力公式σ=MyI ，基于地基反力法可知，桩身弯矩 M 是一个与水平荷载及桩身深度有关的函数，本文主要分析截面的应力，故只需假设M为一个常量，y为X形截面上点到轴的距离，选取如图 2所示的 1～3三个点作为研究点。各应力公式为

2.2 算例分析

为了分析X形异形截面在任意水平向荷载作用下的应力分布规律，建立典型X形桩截面进行算例分析，具体截面设计参数见表1。为便于分析，基于地基反力法可知在同一个横截面里弯矩 M 为一定值，大小由外界水平荷载以及桩身深度决定（算例中取M = 100 kN⋅m）。沿用材料力学符号规定：正号为受拉、负号为受压。

表1 现浇X形桩与圆形桩、方形桩设计参数Table1 Design parameters comparative between XCC pile,circular pile,and square pile

由图3可见，位置点2应力值随着水平向荷载方向与x轴的夹角α的增大（考虑到对称性α只需取0到45°）而逐渐减小，当α = 45°时达到最小。同一方向水平荷载作用下，位置点 2的应力值最大，位置点3的应力值最小，在实际工程中为了避免点2的应力过大，建议在点2处采用圆角过渡或者适当的配上少量钢筋，以避免点2边角处破坏，混凝土脱落，影响 X形桩的力学性能。由图 4可见，水平荷载沿着与X轴夹角为45°时X截面边缘应力分布比 45°时相对要均匀一些，应力集中的现象要弱一些，因此，在承受水平荷载时可以考虑采用与X夹角为45°时的加载方式。

图3 不同加载方式引起的3点的应力变化规律Fig.3 Stress variation on three points under different lateral loading model

图4 X形截面边缘应力分布规律Fig.4 Stress distribution of X-shape cross-section edge

3 X形横截面与圆、方形截面应力分布规律对比分析

基于式（3）可以算出X形截面与圆形截面、方形截面应力分布，比较等截面情况下它们的应力分布规律以突出X截面的优势。由图5可见，在等面积情况下，X形桩截面、圆形截面和方形截面的最大应力分布分别为为5.18，12.18、22.31 MPa，X形截面的最大应力值明显小于另外两种截面形式，因此，在保持混凝土用量一定的情况下，X形截面相比另外两种截面具有很大优势。

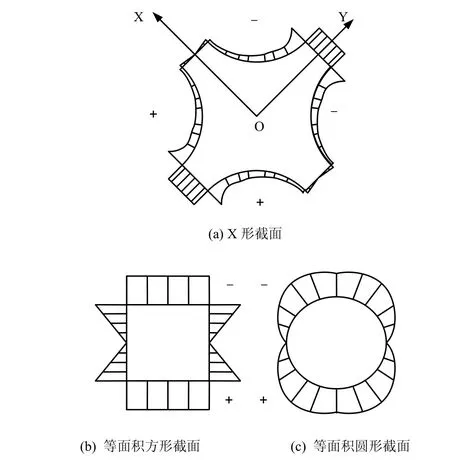
图5 水平荷载作用下截面周边应力分布Fig.5 Stress distributions around section under lateral load

4 X形桩截面形式优化分析

依据惯性矩公式以及材料力学知识，假设水平荷载与X轴夹角为45°，研究保持面积和周长不变时X形截面几何参数的变化对截面应力分布的影响规律，再根据应力分布，归纳得到最优的几何截面设计参数。

4.1 等X形截面面积情况

在等X形截面面积情况下，研究θ = 45°、60°、90°、120°、135°时 a、b的变化对截面最大应力的影响。

由图6可见，在控制截面面积一定时，随着开弧角度的减小截面最大应力在不断减小；随着外包圆直径的不断增大，应力不断减小；随着开弧间距的不断减小，应力不断减小。在实际工程中，保持混凝土用量一定的情况下，对于水平荷载作用下的X桩，为避免截面的应力过大造成的桩身混凝土的破坏，应当尽量使得外包圆直径大一些，开弧角度和开弧间距小一些。考虑到充盈系数等其他因素实际工程中可以采用110°～130°的开弧角度，对于开弧间距也不应太小，否则，会给施工带来不便，建议取0.1～0.2 m左右，外包圆直径建议取0.5～0.7 m左右。

4.2 等X形截面周长情况

在等X形截面周长情况下，研究θ = 45°、60°、90°、120°、135°时 a、b的变化对截面最大应力的影响。

由图7可见，保持截面周长不变时，随着开弧角度的不断减小，截面的应力逐渐减小，随着开弧间距的减小，应力不断减小；随着开弧间距的增大，应力不断减小，这与等面积时的变化情况是一致的。图中135°的曲面出现凹凸不平，是由于控制周长不变，开弧角度为135°，且外包圆直径变化时，开弧间距出现负值，显然这不符合实际，实际的取值必须是正的，并且要小于外包圆直径的值。

图6 X形截面最大应力随截面参数的变化规律（等面积）Fig.6 Maximum stress values of X-shape versus section parameters with the same area

图7 X形截面最大应力随截面参数的变化规律（等周长）Fig.7 Maximum stress values of X-shape versus section parameters with the same perimeter

5 结 论

（1）水平荷载沿着与X轴夹角为45°时X截面边缘应力分布比 45°时相对要均匀一些，应力集中的现象要弱一些。在承受水平荷载时可以考虑采用与X轴夹角为45°时的加载方式。

（2）水平荷载作用下等面积的 X形截面最大应力仅为圆形截面和方形截面的25%～50%，由此表明 X形截面形式优于等面积圆形截面和方形截面。

（3）水平荷载作用时，等面积情况下X形桩截面的应力随着外包圆直径、开弧角度的增大而减小，随着开弧间距的减小而减小；等周长情况下，X形桩截面的应力随着外包圆直径的增大而减小，随着开弧间距、开弧角度的减小而减小。实际工程中，建议外包圆直径可以取0.5～0.7 m左右，开弧间距取0.1～0.2 m左右，开弧角度采用110°～130°左右。

[1]刘云飞,朱永华. 水平受荷桩的截面优化设计[J]. 特种结构,2004,21(4): 16－18.LIU Yun-fei,ZHU Yong-hua. Cross section optimum design of laterally-loaded pile[J]. Special Structures,2004,21(4): 16－18.

[2]吴泽军,耿大新,方焘. 变截面桩的水平荷载模型试验研究[J]. 铁道建筑,2011,(8): 103－105.WU Zhe-jun,GENG Da-xin,FANG Tao. Study on behaviour of stepped cross-section pile under lateral loading by model test[J]. Railway Engineering,2011,(8):103－105.

[3]胡培进,汪中卫,李强. 变截面桩的力学性能及工程意义[J]. 上海地质,2007,108(3): 27－31.HU Peng-jin,WANG Wei-zhong,LI Qiang. Mechanical property and engineering significance for variable crosssection pile[J]. Shanghai Geology,2007,108(3): 27－31.

[4]石庆瑶,王成. 水平荷载作用下长桩的合理截面形式优化研究[J]. 岩土力学,2008,29(增刊): 650－654.SHI Qing-yao,WANG Cheng. Research on reasonable section type of long pile loaded laterally[J]. Rock and Soil Mechanics,2008,29(Supp.): 650－654.

[5]张永谋,闫强刚. 受横向动载的空心桩性能研究[J]. 兰州交通大学学报,2010,29(6): 10－15.ZHANG Yong-mou,YAN Qiang-gang. The dynamical calculation of laterally loaded hollow pile[J]. Journal of Lanzhou Jiaotong University,2010,29(6): 10－15.

[6]詹金林. 水平或竖直受荷壁板桩群桩的变分法分析[D].南京: 河海大学,2006.

[7]贺杰. Y形桩水平承载性能试验研究[D]. 南京: 河海大学,2007.

[8]袁佶. X形钢筋混凝土桩水平承载性能足尺模型试验研究[D]. 南京: 河海大学,2009.