基于重心法的粮食配送中心选址研究＊

魏 军，皮安涛，张加华

(长沙理工大学交通运输工程学院，湖南长沙 410004)

基于重心法的粮食配送中心选址研究＊

魏 军，皮安涛，张加华

(长沙理工大学交通运输工程学院，湖南长沙 410004)

我国粮食产业的现状是粮食产区及种类分布不均衡，虽然粮食产量在增长但其中存在的物流问题还比较严重，主要问题是粮食储运成本高、效率低、损耗大，解决这一问题的关键在于粮食配送中心的合理选址.使用重心法选址能够降低粮食运输成本，提高粮食流通效率，实例证明了重心法应用于粮食配送中心选址的可行性.

粮食物流;配送中心;选址方法;重心法

据国家统计局公告，2010年我国粮食总产量为54641万吨(10928亿斤)，比上年增加1559万吨，增产2.9%.其中，夏粮播种面积27421千公顷，扩大38.4千公顷，夏粮总产量为12310万吨，比上年减少39万吨;早稻播种面积5794千公顷，比上年减少76.1千公顷，早稻总产量为3132万吨，比上年减少204万吨;秋粮播种面积76657千公顷，比上年增加924千公顷，秋粮总产量初步统计为39199万吨，比上年增加1801万吨.其中，上海、浙江、广东、福建、海南、北京、广西、甘肃、青海、四川都处于粮食净缺口区，特别是四川由于大量劳动力外出导致粮食由输出变为输入，缺口总计高达675亿公斤.内蒙、山东、东北三省、河南、河北、湖北、江西为粮食输出地，输出为3300亿公斤，其中东北三省占了1000亿公斤.

1 粮食物流问题分析及解决方法

由上述统计可以看出，我国粮食产量在增长，但是粮食产区及种类分布不均衡，粮食物流在时空分布上跨度极大，又由于目前我国粮食物流体系建设滞后导致粮食储运成本高、效率低、损耗大等问题比较突出.据国家粮食局调查，中国粮食产后损失8% －10%，主要原因在于粮食产后储藏、运输等方面不科学，其中，主要是储粮损失，全国每年仅农户储存粮食损失即达1500万吨至2000万吨，造成损失180亿到240亿元;粮食收购市场放开后，农户存粮的时间延长到全年储存，由仓储中心设置不合理、仓储设施条件差造成的粮食产后损失更为巨大，因而发展现代粮食物流产业已经刻不容缓.依靠现代信息技术，国内许多学者对粮食物流体系做出了研究，许德刚在研究了我国智能化粮食物流系统现状的基础上对国内粮食物流的发展趋势进行了探讨［1］;孙吉贵、白洪涛等设计并实现了粮食调拨决策支持系统［2］.他们的研究成果很大程度上对国内粮食物流发展起到了一定的指导作用.

在粮食物流系统中，粮食配送中心处于枢纽位置，它是粮食流通过程中的一个重要节点，是一种多功能的粮食配送设施，合理的选择粮食配送中心的位置可以有效地解决粮食储运成本高、效率低、损耗大等问题，保障粮食物流系统的平稳发展.因此，粮食配送中心的选址决策在粮食物流体系优化中占有十分重要的位置，在选址过程中应考虑以下影响因素:

①粮食供需状况.这是粮食配送中心配送的对象，必须搞清楚粮食来源和去向的分布情况、过去和现在以及将来的发展等.配送中心应尽量与生产地和需求地实现短距离优化.

②交通运输条件.粮食配送运量较大，配送中心的选址应靠近交通运输枢纽，条件允许的情况下，还应尽量靠近铁路货运站、港口及公路.

③用地条件.在土地价格日益昂贵的今天，配送中心的占地问题也显得十分重要，建设配送中心要综合考虑土地价格及政府的交通规划要求.

④运输与服务的方便程度，粮食配送中心选址应靠近粮食加工厂及居民区，以便缩短运输距离，降低运输成本.

⑤投资额限制情况，粮食配送中心选址还应考虑所在地区是否有相关优惠政策及是否有投资额的限制等情况.

2 粮食配送中心选址模型

2.1 配送中心选址方法及特点

配送中心选址的方法有很多，主要分为两类:定性分析法和定量分析法.

2.1.1 定性分析法

定性分析法主要是根据选址影响因素和选址原则，再依据专家或管理人员的丰富经验、知识等进行综合分析，最终确定配送中心的具体位置.这类方法主要有专家打分法、德尔菲法.定性分析法的优点是注重历史经验，简单易行.其缺点是容易犯经验主义和主观主义的错误，并且当可选地点较多时，不易做出理想的决策，导致决策的可靠性不高.

2.1.2 定量分析法

定量分析法主要包括重心法［3，4］、鲍莫尔－沃尔夫法、运输规划法、Cluster法、CFLP法、数值分析法、双层规划法、遗传算法［5］、蚁群算法［6］等.定量分析法选址的优点是能求出比较准确可信的解.缺点是计算比较复杂，并且很难求出最优解.

2.2 基于重心法的粮食配送中心选址

本文根据粮食配送中心选址的特点对选址问题进行了研究，基于考虑到重心法能使运输成本达到最小化，故采用重心法进行选址.重心法的原理是将物流系统中的需求点和资源点看成是分布在某一平面范围内的物流系统，各点的需求量和资源量分别看成是物体的重量，物体系统的重心作为物流网点的最佳设置点.其优点是可以在没有备选地点的情况下进行选址，并且运算简单，能够为管理者和决策者提供理论上成本最低的配送中心地点，从而拟定初步布局方案，符合粮食配送中心的选址要求.

2.2.1 重心法数学模型

重心法模型的建立有一定的前提条件，条件如下:

①不同地点的建设、管理及运营费用相同;

②配送中心与粮食生产地及粮食需求地之间的距离是直线距离;

③配送车辆在行驶过程中是匀速的;

④粮食产量和粮食需求量平衡.

其模型具体建立过程表述如下:

设有n个点分别代表粮食生产地和粮食需求地，各自有一定量粮食需要以一定的运输费率运到位置待定的配送中心，或者从配送中心运出，那么可以建立以下的模型来确定该配送中心的位置:

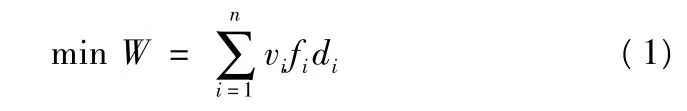
式中:W—粮食运输总成本;vi—i点的粮食运输量;fi—配送中心到i点的运输费率;di—配送中心到i点的运输距离.

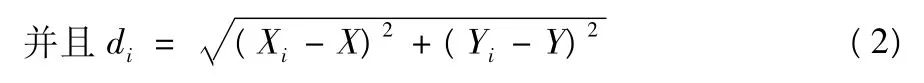
其中(Xi，Yi)—粮食生产地或粮食需求地i的坐标;(X，Y)—待定配送中心的坐标.

2.2.2 重心法求解方法

该模型采用迭代法求解，迭代之前应先算出配送中心的初始地址(X0，Y0)

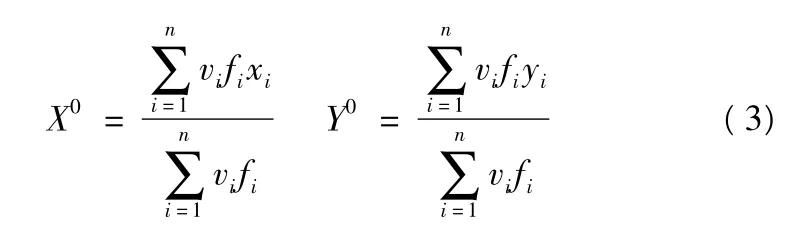
再引入以下迭代公式求最优解

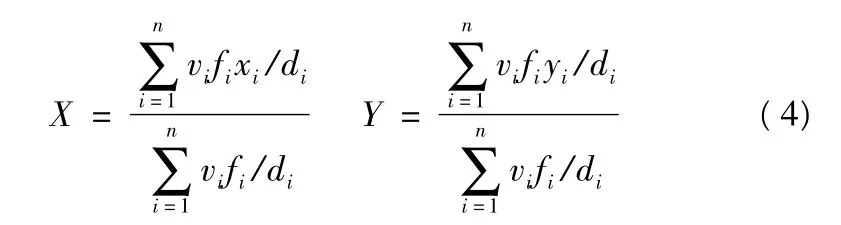
具体求解步骤如下:

①根据公式(3)求出配送中心初始地址(X0，Y0);

②将(X0，Y0)分别代入公式(2)和(1)求出总运费w0;

③将(X0，Y0)分别代入公式(2)和(4)求出优化地址(X1，Y1);

④将(X1，Y1)分别代入公式(2)和(1)求出总运费w1，比较w1与w0的大小.若w1＜w0，则重复步骤③、④继续迭代;若w1=w0，则停止迭代，即(X1，Y1)为最优解.

3 算例分析

设某区域内有A，B两个粮食生产基地，C，D，E三个粮食需求地，各点平面位置如图1所示，具体产量、需求量、坐标及运输费率如表1所示，寻求配送中心的最佳位置使粮食运输成本达到最低.

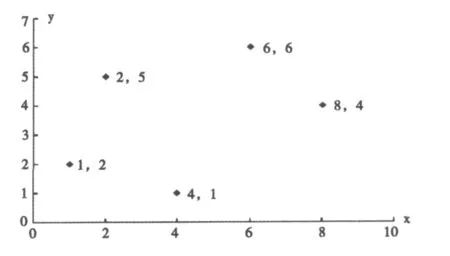
图1 各点平面分布图

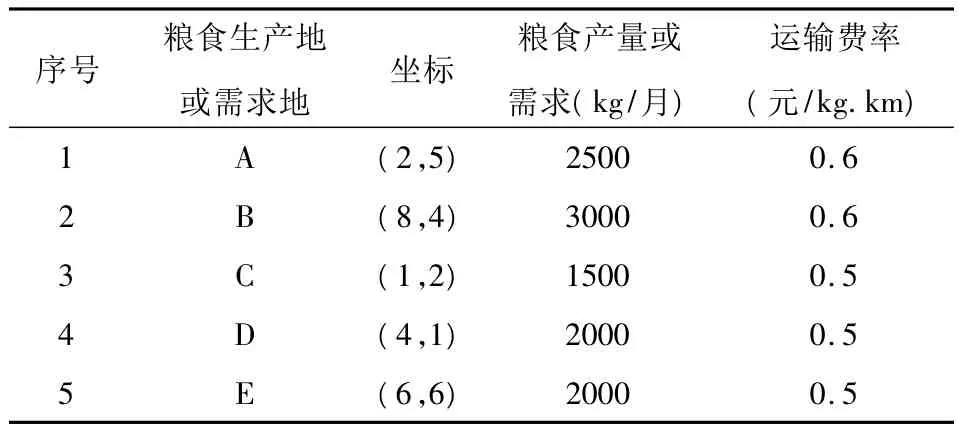
表1 各点的坐标、产量或需求量及运输费率

根据上述模型进行计算，计算结果见表2.

由图2可以看出随着迭代次数的增加，运输成本在逐渐降低，易看出成本最低的配送中心坐标为(4.7809，4.0334)，故可以将粮食配送中心修建在这个地点或附近以实现效益最大化.

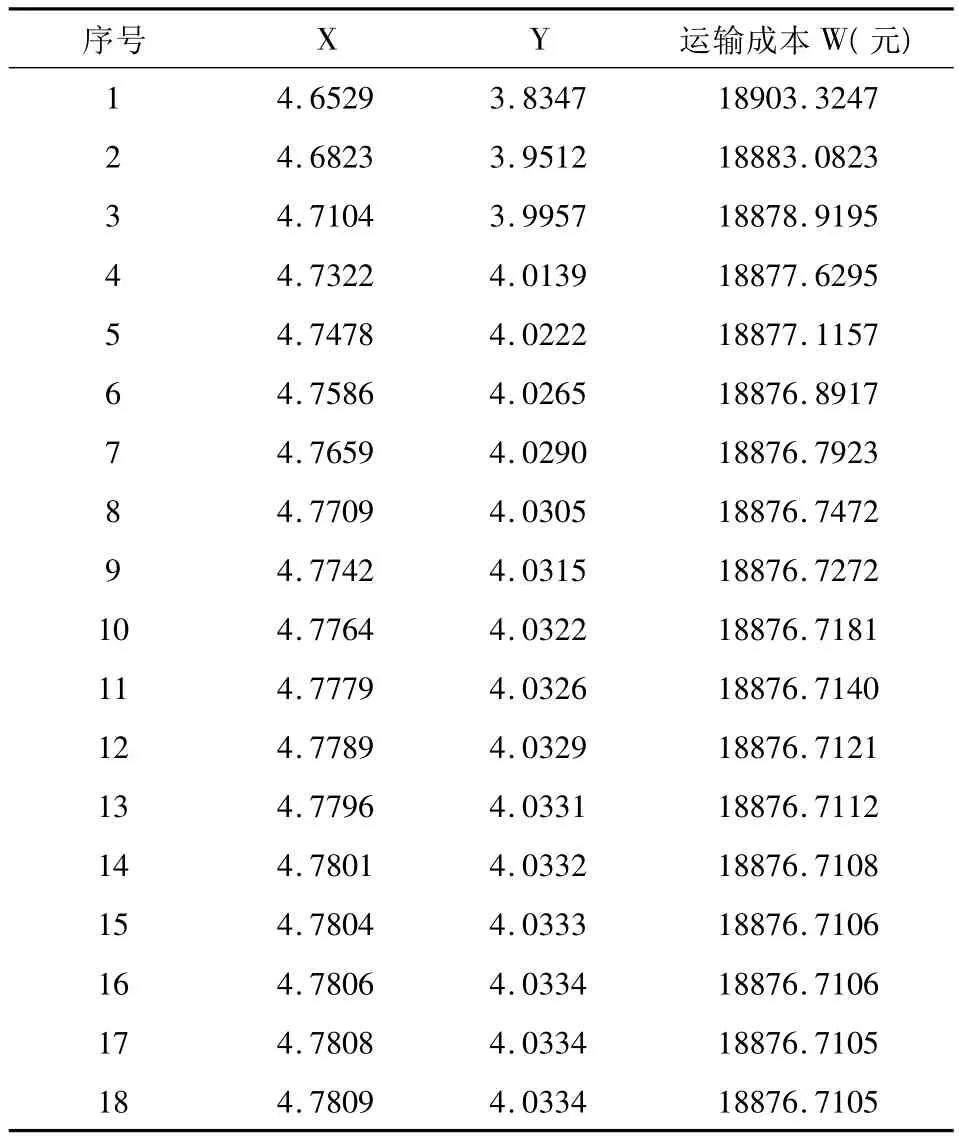
表2 配送中心坐标及运输成本

为了更直观地观看，根据上表生成了图2.

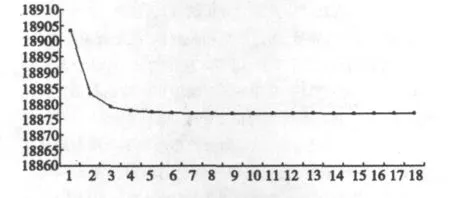
图2 运输成本变化趋势

4 结论

粮食配送中心是粮食流通过程中的重要一环，合理的选址能够提高粮食流通效率，降低物流成本，提高粮食企业的经济效益.本研究采用的重心法虽然能得到理论上的成本最低地点，但是由于重心法自由度较大，在实际中很难得到最优的地点，因为这个最优地点在实际中很可能位于湖泊、河流或者其他无法修建配送中心的地区，所以在实际粮食配送中心选址中还应综合考虑交通便利条件、环境条件等因素，在所求的最优地点附近选择更合适的位置.

［1］许德刚.智能化粮食物流系统现状及发展趋势［J］.河南工业大学学报(自然科学版)，2009，(2):13 －17.

［2］孙吉贵，白洪涛，于海鸿，等.粮食调拨决策支持系统的设计与实现［J］.吉林大学学报(信息科学版)，2005，(1):81 －85.

［3］杨茂盛，姜华.基于重心法与离散模型的配送中心选址研究［J］.铁道运输与经济，2007，(7):68 －70.

［4］毛太田，陈英武.一种基于重心法的连锁经营企业区域物流配送中心选址模型［J］.工业工程，2008，(3):123－126.

［5］王春燕，张华.遗传算法在配送中心选址中的应用［J］.物流科技，2007，(4):111 －112.

［6］潘磊.基于蚁群算法和人工神经网络的物流配送中心选址决策［J］.中国储运，2008，(8):113 －114.

U492.3

A

1008－4681(2012)02－0087－03

2012－02－28

魏军(1986－)，男，湖北天门人，长沙理工大学交通运输工程学院硕士生.研究方向:交通运输规划与设计.

(责任编校:晴川)