关于三次样条插值的教学研究*
2012-11-07张希娜李亚红郭中凯
张希娜,李亚红,郭中凯
(兰州理工大学技术工程学院,甘肃 兰州 730050)
关于三次样条插值的教学研究*
张希娜,李亚红,郭中凯
(兰州理工大学技术工程学院,甘肃 兰州 730050)
三次样条函数作为最常用的插值函数是数值分析教学中的重点和难点.从简单例子出发讲解了三次样条插值函数的定义及其第一类和第二类边界条件的判定,并将其推广到含n个节点的情况.旨在将抽象理论具体化,易于学生理解和接受.
三次样条插值;边界条件;例子
传统本科教材中,三次样条插值函数这部分内容一般都强调理论.而理论性过强,内容过于抽象,在教师讲解过程中,学生很难理解,从而抑制了学生学习的积极性和主动性,影响了学生对三次样条插值的掌握,不利于学生对这部分内容的应用,从而影响了学生创新意识和创新能力的培养.
1 三次样条插值的教学改革思想
针对这种情况,为了使学生更容易接受这部分内容,激发学生学习三次样条插值的兴趣,加深他们对三次样条知识的理解和认识,本文提出从最简单的例子出发,讲解三次样条插值的三种边界条件.
2 三次样条插值教学过程实践
讲解这部分内容之前,我们着重要介绍分段线性插值和分段三次埃尔米特插值.分段线性插值是在给定了插值节点上的函数值以后,构造一个整体连续的函数.而分段三次埃尔米特插值是在给定了插值节点上的函数值和微商值以后,构造一个整体上具有一阶连续微商的插值函数,它是光滑的分段插值.三次样条插值把整体光滑度再提高,它是在只给出插值点上的函数值的情况下构造一个整体上具有二阶连续微商的插值函数.首先,我们来看一下三次样条插值函数的定义[1]:
定义:给定[a,b]上n+1个节点a=x0<x1<… <xn-1< xn=b以及这些点上的函数值 f(xi)=yi(i=0,1,…,n).若函数 s(x) 满足:1)s(xi)=yi,i=0,1,…,n;2) 在每个小区间[xi,xi+1]上是一个不超过三次的多项式;3)s(x)、s'(x)、s″(x) 在[a,b]上都连续.则称 s(x) 为函数 f(x) 关于节点x0,x1,…,xn的三次样条插值函数.
以上定义从直观上比较难理解,下面我们从一些实例出发,帮助学生理解什么样的函数是三次样条函数.
例:试判断下列函数是否为三次样条函数:
下面我们通过两个简单的实例给大家介绍一下三次样条插值函数的两类边界条件,由此引出n个节点的三类边界条件,这就是一般教材上的三次样条插值理论[2].
例1:求满足 f(-1)= -1,f(0)=0,f(1)=1,f'(-1)=0,f'(1)=-1的三次样条插值函数S(x).
解:三个节点 x= -1,0,1构成两个区间[-1,0]和[0,1].设f'(0)=m,三次样条插值函数是特殊的分段三次埃尔米特插值,关键是构造插值基函数.
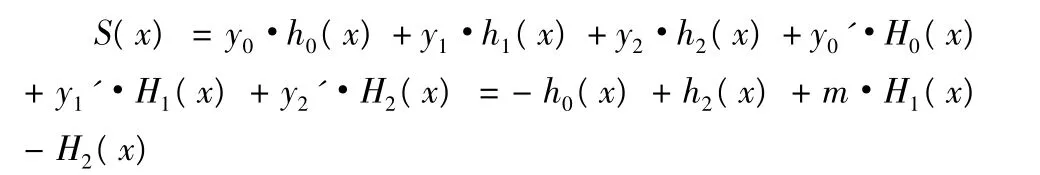
由分段三次埃尔米特插值的公式:
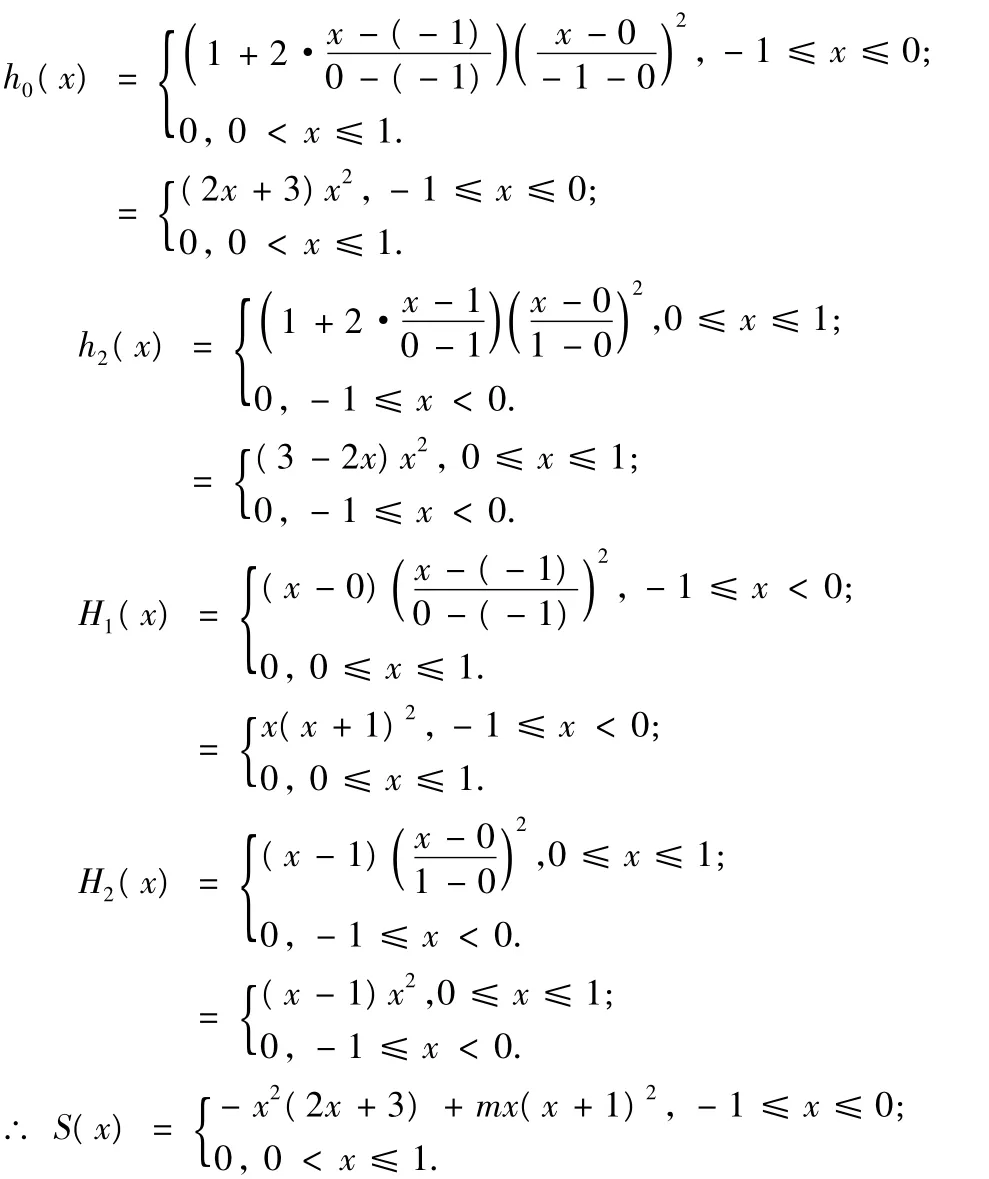
先求一阶导数,再求二阶导数:
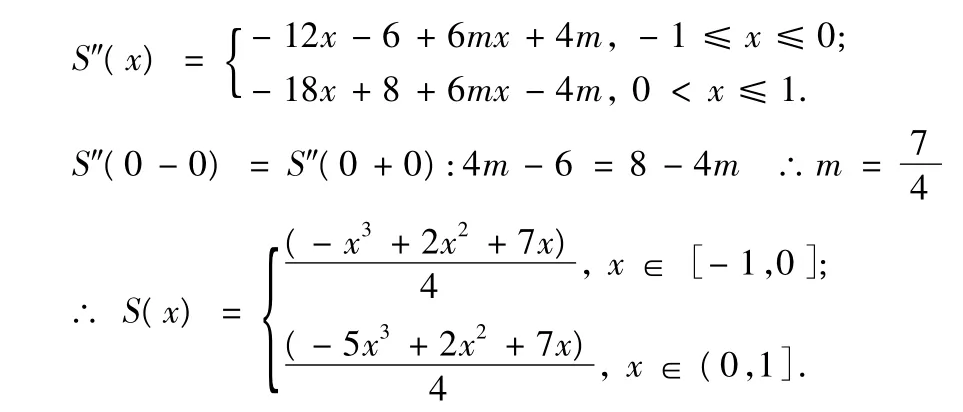
分析:本题中有三个节点,已知三个节点处的函数值和两个端点处的微商值,类似于这样的已知条件,我们称为三次样条插值的第一类边界条件.
例2:已知函数在节点 x=0,1,2,3 处的值均为 0,求满足边界条件 S″(0)=1,S″(3)=0 的三次样条插值函数S(x).
解:已知及所设如以下表格所示:
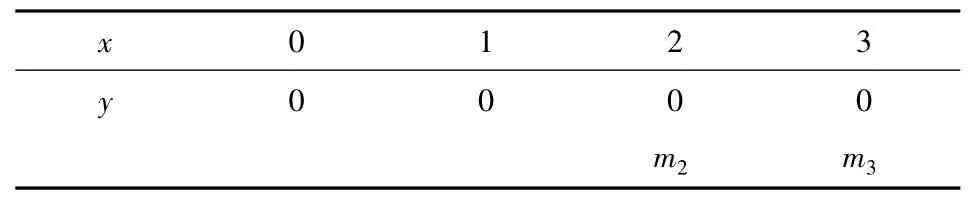
x 0123 y 0000 m2 m3


分析:本题中有三个节点,已知三个节点处的函数值和两个端点处的微商值,类似于这样的已知条件,我们称为三次样条插值的第二类边界条件.
由以上两个例子,我们引出一般的三次样条插值函数的边界条件(含n个节点):
第一类边界条件:已知S'(x0)=m0及S'(xn)=mn.
第二类边界条件:已知
对于这种含n个节点的一般性三次样条插值问题,我们的解题思路与以上两个例题类似.我们联系三次样条插值的定义,又已知节点处的函数值.我们像例题中那样,先根据分段三次埃尔米特插值设出S(x).对于第一类边界条件来说,我们设出剩余的中间n-1个节点处得微商值,解决这些微商值,是我们解题的目标.通过设出的微商值和已知条件,我们可以设出S(x),再依次求S'(x)、S″(x),再根据样条函数的二阶导数的连续性,可列方程组S″(xi-0)=S″(xi+0),i=1,2,…,n-1.由n-1个未知数n-1个方程,通过线性代数解方程组的知识,可解出最终结果.对于第二类边界条件,我们设出所有n个节点处的微商值,我们的任务就是解出这些微商值.同样,通过这些设出的微商值与已知的函数值,再依次求S'(x)、S″(x),再根据样条函数的二阶导数的连续性,可列方程组 S″(xi-0)=S″(xi+0),i=1,2,…,n -1 及已知条件 S″(x0)=S″(xn)=0.这样n+1个未知数n+1个方程,通过解方程组的知识,可得所求结果.
一般理论中,还有第三类边界条件:已知函数y=f(x)为周期函数,基本周期为b-a=xn-x0,y0=yn.相应要求样条函数S(x)也是周期函数,满足已知S'(x0)=S'(xn)和S″(x0)=S″(xn).对于此第三类边界条件,解决思路与前两种边界条件相似.设出所有n个节点处的微商值,联系已知的函数值,再依次求S'(x)、S″(x),再根据样条函数的二阶导数的连续性,可列方程组 S″(xi- 0)=S″(xi+0),i=1,2,…,n - 1 及已知条件 S″(x0)=S″(xn) 和 S'(x0)=S'(xn),这样n+1个未知数n+1个方程,通过解方程组的知识,即可求出.
对于三次样条插值函数来说,当插值节点逐渐加密时,不但样条插值函数收敛于函数本身,其微商也收敛于函数的微商,提高了函数的光滑性,比之前所讲的分段三次埃尔米特插值还要优越.因此,在航空、造船等很多工程技术领域有重要而又广泛的应用.最后指出,样条函数不一定必须是逐段三次多项式,也可以是逐段简单函数,只要保持连接点足够光滑[3].因三次多项式计算简单,且满足一般实际问题的要求,因而应用最为广泛.
[1]张池平.计算方法[M].北京:科学出版社,2006.
[2]徐萃微.计算方法引论[M].北京:高等教育出版社,1985.
[3]李庆杨,王能超,易大义.数值分析[M].武汉:华中工学院出版社,1982.
O24
A
1008-4681(2012)02-0131-02
2012-01-12
张希娜(1983-),女,河南商丘人,兰州理工大学技术工程学院助教,硕士.研究方向:马尔可夫骨架过程.
(责任编校:晴川)
