高超声速滑翔飞行器约束预测校正再入制导

王智, 唐硕, 闫晓东

(西北工业大学 航天学院, 陕西 西安 710072)

高超声速滑翔飞行器约束预测校正再入制导

王智, 唐硕, 闫晓东

(西北工业大学 航天学院, 陕西 西安 710072)

针对大升阻比高超声速滑翔飞行器的再入制导问题,将再入轨迹划分为初始下降段、过渡段和准平衡滑翔段。初始下降段采用定倾侧角飞行,过渡段在最大倾侧角附近飞行,准平衡滑翔段利用数值预测校正方法和准平衡滑翔条件在线设计同时满足过程约束和终端约束的倾侧角制导律。通过标准条件和扰动条件下的仿真结果表明,这种制导律在满足各种约束的条件下,不仅能够达到较高的精度,而且对初始误差具有良好的鲁棒性,能够应付再入时各种不确定性因素的影响。

再入制导; 预测校正; 准平衡滑翔; 高超声速滑翔飞行器

引言

高超声速滑翔飞行器具有升阻比大、任务目标多样化、气动加热强等特点,面临的飞行环境也复杂多变,给飞行器的制导系统提出了很高的要求。为了提高制导方法的适应性,需要采用适应能力更强的在线轨迹规划方法、预测校正制导方法,从而可以较好地满足高超声速滑翔飞行器的制导需求。

预测制导最早由Schultz等人[1]于1967年提出,此方法利用纵程与横程预测方程对相关参数进行预报,但受航迹角影响较大,且对地球旋转只能做简单修正,不宜用于飞行时间较长的飞行器制导。Joshi[2]提出了一种考虑路径约束的数值预测制导算法,即当预测的飞行轨迹超出阻力边界时调整倾侧角,其调整量由控制律决定,修正后的控制量用于迭代校正,从而保证预测轨迹满足路径约束。Ping Lu[3]研究了倾侧角参数化问题,并提出了一种针对低升阻比再入飞行器的预测制导方法。

本文根据再入轨迹特点,将再入轨迹分为三段:初始下降段、过渡段和准平衡滑翔段。利用改进的准平衡滑翔条件将飞行过程约束转化为控制变量的边界约束,从而将再入制导设计转化为单参数搜索问题,提高轨迹在线规划速度。

1 再入动力学模型

1.1 三自由度无量纲运动方程

在不改变问题实质的情况下,为研究问题方便,考虑球型、自转、无风的地球模型。假设飞行器无侧滑,为提高数值预测落点的效率,建立三自由度无量纲再入运动方程,如式(1)所示[4]。

(1)

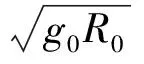
在飞行过程中,攻角由攻角-马赫数函数确定,方程中唯一的控制量是倾侧角。

1.2 飞行约束

1．2．1过程约束

再入过程约束主要考虑热流约束、过载约束、动压约束和准平衡滑翔约束,其表达式如式(2)～式(5)所示[5]。

(2)

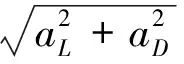
(3)

(4)

(5)

1．2．2终端约束

高超声速飞行器是一种远程精确制导飞行器。再入滑翔制导后为末制导,因而再入滑翔制导的终端应满足末制导的要求。取终端约束为:

(6)

式中,e=1/r-v2/2;Δψ为航向角误差,是航向角ψ与相对目标点的视线角ψLOS的差值。

1.3 再入走廊

1．3．1高度-速度剖面再入走廊数学模型

将指数大气密度公式,即

ρ[(r-1)R0]=ρ0e-β(r-1)R0

(7)

代入式(2)～式(5),可得高度-速度剖面内再入走廊边界数学模型,即

(8)

式中,rQEGC无解析解,需要迭代求解,即给定速度v,由式(5)取等号并令σEQ=0对应的非线性方程求rQEGC。从而高度-速度剖面的再入走廊可以表示为:

(9)

1．3．2倾侧角大小边界

利用准平衡滑翔条件可以将再入走廊的约束转换为控制变量的约束。当给定v时,将rdown,rup代入式(5)即可解出倾侧角大小的边界值|σ|min(v),|σ|IQEGC,max(v),并有以下关系:

(10)

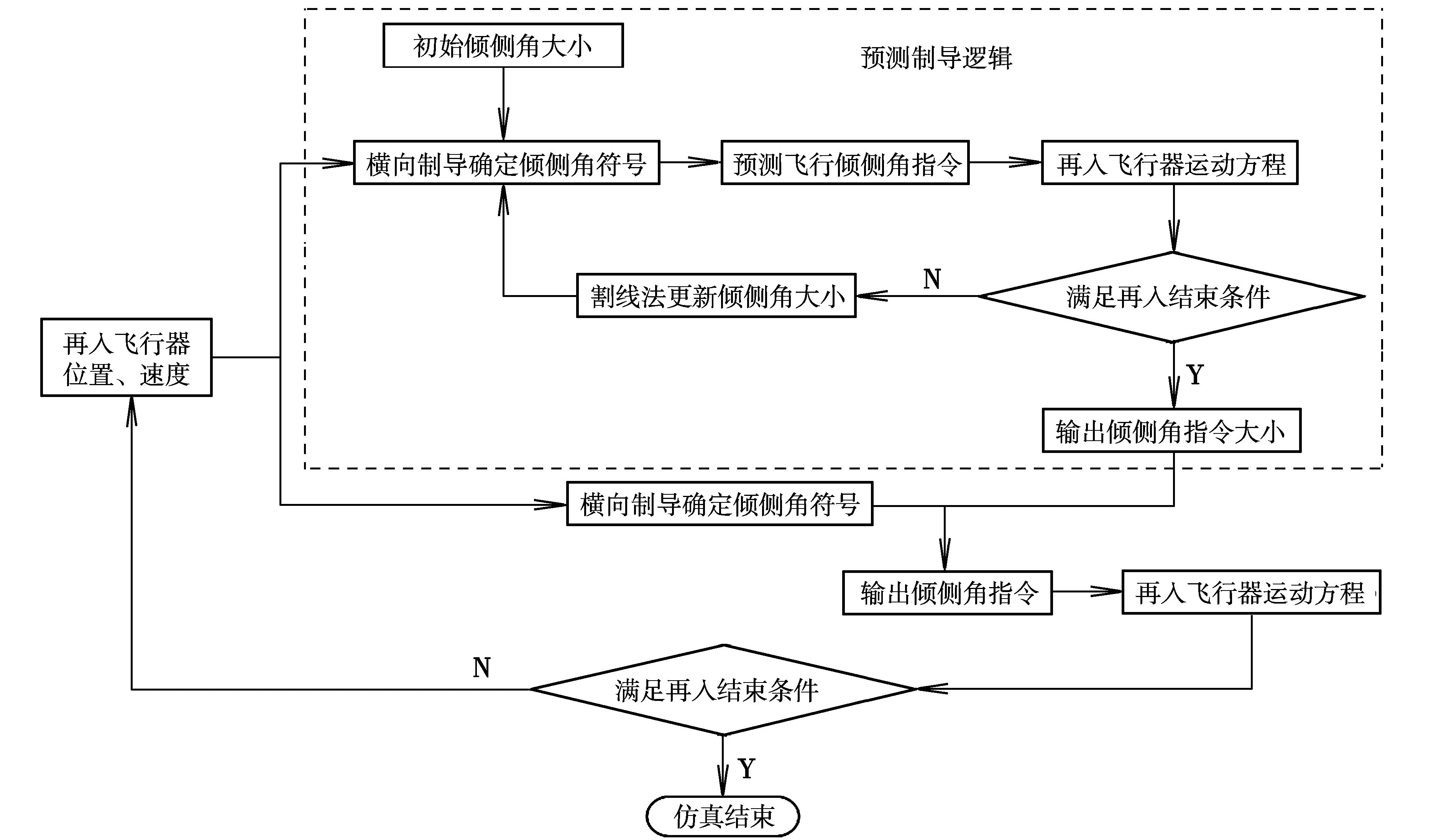
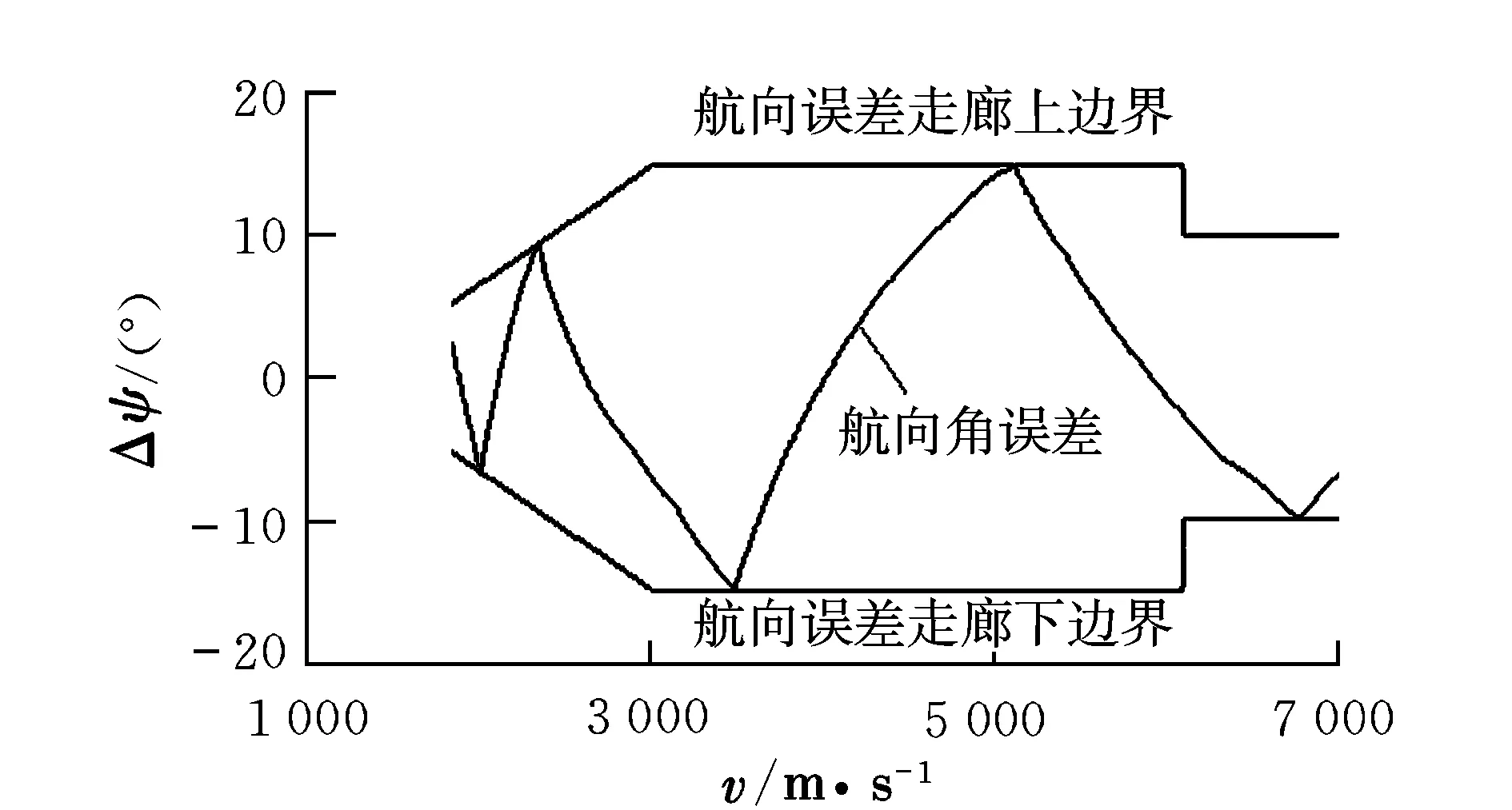
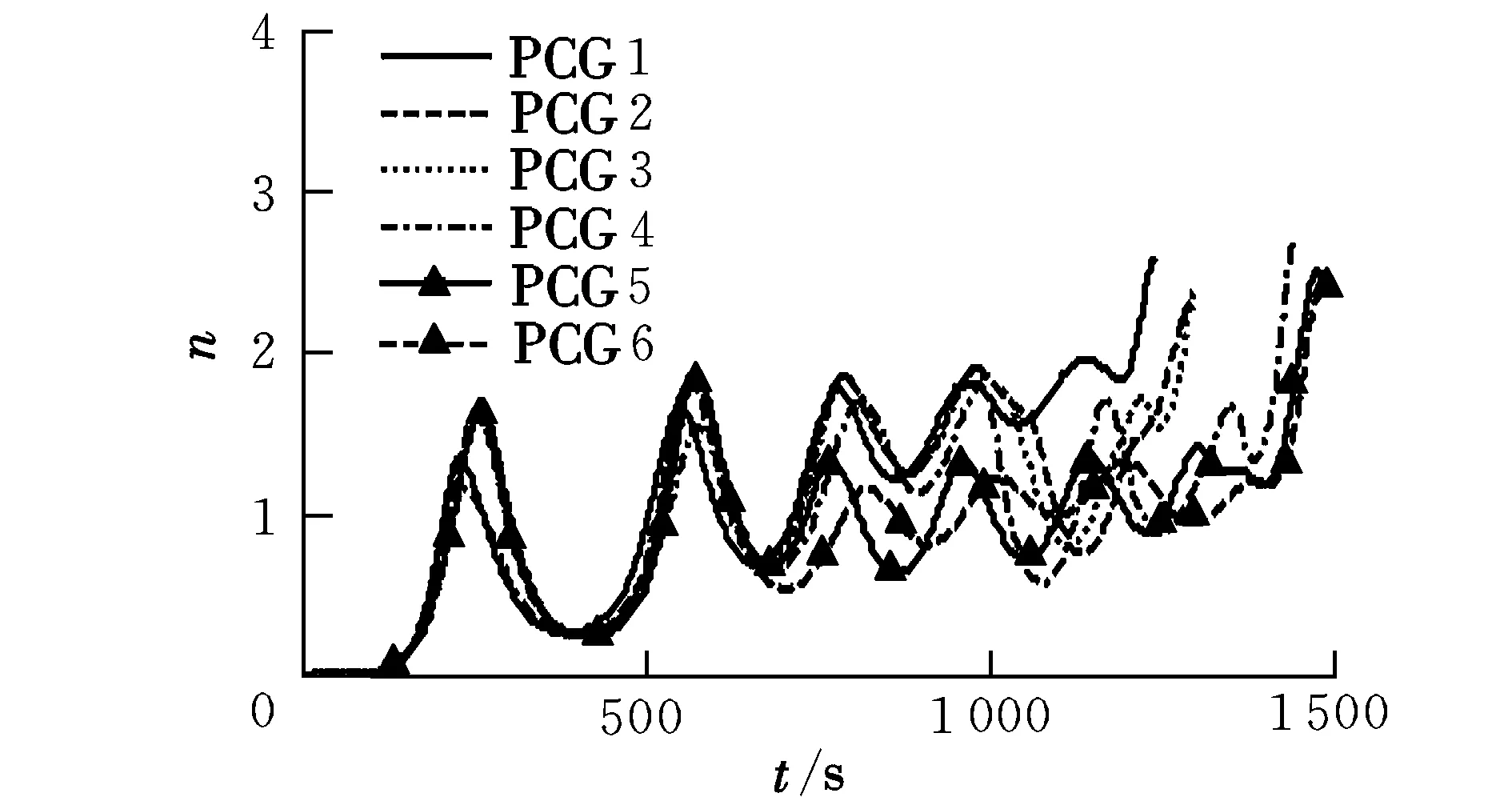
为了满足再入末端对倾侧角大小|σ|的要求,引入速度参数vlr,当满足vf≤v

|σ|max(v)=

(11)

从而再入过程倾侧角大小的上下边界满足如下关系:

|σ|min(v)≤|σ(v)|≤|σ|max(v)

(12)

2 数值预测校正制导

根据高超声速再入飞行器再入弹道特点,将再入弹道分为初始下降段、过渡段和准平衡滑翔段。

2.1 初始下降段

高超声速滑翔飞行器从临近空间再入,再入高度较高,飞行器所受到的气动力十分小。随着高度的下降,飞行器从稀薄大气层向稠密大气层过渡,高度快速下降,速度变化不大,将这段气动控制力弱的飞行段称之为初始下降段。由于初始下降段的气动力小,所以该段主要采用开环制导方式,采用常值倾侧角σ0。σ0的符号由下式确定:

sgn(σ0)=-sgn(Δψ0)

(13)

倾侧角的大小|σ0|通过迭代求解,迭代准则是使初始下降段的纵向轨迹进入再入走廊并平滑地转换到准平衡滑翔状态,即

(14)

式中,(dr/dv)3DOF=vsinγ/(-aD-sinγ/r2);(dr/dv)QEGC为高度-速度再入走廊中准平衡滑翔边界的斜率,可通过有限差分得到。

2.2 过渡段

大升阻比高超声速飞行器再入时,再入轨迹在高度方向存在比较大的振荡,这种大气密度的反复变化是控制系统所不期望的,因此在初始下降段与准平衡滑翔段之间引入过渡段。过渡段开始于初始下降段末端,当高度出现第一个波峰时初始下降段结束。过渡段飞行器在最大倾侧角附近飞行,即

|σ(v)|=|σ|max(v)-C

(15)

式中,C为一常数;同时σ(v)的大小满足式(12)的约束,符号sgn(σ)由侧向制导确定。

2.3 准平衡滑翔段

准平衡滑翔段是高超声速飞行器的主要飞行段和制导段。在每一个制导周期内,给定初始倾侧角大小|σ|,其符号由航向误差走廊决定,从当前点积分运动方程(1),且积分过程中|σ|仍受式(12)约束,倾侧角符号由侧向制导决定。从而当到达再入段末端时,即e=ef时,可得如下待飞航程偏差:

f(|σ|)=Stogo(ef)-Stogo,f=0

(16)

因此可以根据预测过程计算的待飞航程偏差计算出一个合适的倾侧角大小|σ*|,使待飞航程偏差为零,即有f(|σ*|)=0。

割线法是计算|σ*|的一种快速有效的方法,即

(17)

一旦找到|σ*|,从而可以得到随速度变化的倾侧角大小剖面|σ(v)|。当前状态的制导指令为倾侧角大小剖面的第一个点给定的倾侧角大小,其符号由侧向制导决定。同样的过程在下一个制导周期重复进行,从而形成闭环制导。制导逻辑如图1所示。

图1 准平衡滑翔段制导逻辑

2.4 基于航向角误差走廊的航向轨迹控制

图2 航向误差走廊示意图

采用航向角误差走廊限定航向角,可以实现大横程条件下的侧向控制。首先给出航向角误差走廊的定义,如图2所示。当航向角误差Δψ大于航向误差的边界,倾侧角反号;在边界区域内,倾侧角保持原来的符号。这样既可以使侧向误差不致过大,也可使再入飞行器具有一定的机动性。

3 仿真验证及分析

3.1 标准条件下的制导方法性能仿真

仿真结果如图3～图7所示。从图3可以看出,任务PCG1～PCG6均可以到达目标点。从图 4可以看到,倾侧角变化平缓,反转次数5次左右。从图5～图7可以看出,再入过程驻点热流率、动压和过载满足要求。

表1 任务PCG1～PCG6的再入初始条件

图3 三维再入轨迹

图4 倾侧角时间历程

图5 驻点热流时间历程

图6 动压时间历程

图7 总过载时间历程

再入末端状态如表2所示。从表2可以看出,预测制导方法的平均制导指令生成时间T约在0.6 s左右,小于制导周期(1 s),算法具有较好的实时性。再入终端均满足要求,验证了所提制导方法的精度和收敛性。

表2 任务PCG1～PCG6的再入末端状态

3.2 扰动条件下的制导方法性能仿真

为验证数值预测校正制导的鲁棒性,下面对再入点轨迹参数存在偏差情况下的制导性能进行分析。任务PCG1再入点轨迹参数偏差边界和主要仿真结果见表 3。

由表 3可以看出,再入点轨迹参数存在偏差的情况下,再入终端条件和飞行约束条件均可以满足,验证了所提制导方法的鲁棒性。

表3 任务PCG1再入点参数扰动条件下仿真结果

4 结束语

通过对仿真结果的分析可知,利用预测校正结合准平衡滑翔条件的方法,将再入轨道分为初始下降段、过渡段和准平衡滑翔段,可以得到高度变化平缓、满足末端精度要求和飞行过程约束的制导律,并通过对初始条件不确定性的仿真,验证了该方法具有较强的鲁棒性。

[1] Schultz R L,Anderson P,Stolaric E.A simple guidance scheme for lifting body reentry vehicle[C]//AIAA 5th Aerospace Sciences Meeting.NewYork,1967:136-145.

[2] Joshi Ashok,Sivan K.Predictor corrector reentry guidance algorithm with path constraints for atmospheric entry vehicles[J].Journal of Guidance,Control,and Dynamics,2007,30(5):1307-1318.

[3] Lu Ping.Predictor-corrector entry guidance for low-lifting vehicles[J].Journal of Guidance,Control,and Dynamics,2008,31(4):1067-1075.

[4] Xue Songbai,Lu Ping.Constrained predictor corrector entry guidance[R].AIAA 2009-5767,2009.

[5] 雍恩米,唐国金,陈磊.高超声速无动力远程滑翔飞行器多约束条件下的轨迹快速生成[J].宇航学报,2008,29(1):46-52.

Constrainedpredictor-correctorreentryguidanceforhypersonicglidevehicle

WANG Zhi, TANG Shuo, YAN Xiao-dong

(College of Astronautics, Northwestern Polytechnical University, Xi’an 710072, China)

For the reentry guidance law design problem of high lift-to-drag ratio hypersonic glide vehicle, reentry trajectory was divided into initial descent phase, transition phase and quasi-equilibrium glide phase. At the initial descent phase, constant bank angle was employed. At the transition phase, maximum bank angle was employed. At the quasi-equilibrium glide phase, a on-line guidance law designed based on numeric predictor-corrector method and quasi-equilibrium glide conditions was presented. The guidance law can generate reasonable bank angle profile which can satisfy the path constraints and terminal constraints. The results of standard initial condition simulation and error initial condition simulation show that the predictor-corrector can not only acquire higher accuracy, but has strong robustness to the initial errors at all constraints to be satisfied, even at the uncertain conditions.

reentry guidance; predictor-corrector; quasi-equilibrium glide; hypersonic glide vehicle

2011-05-20;

2011-09-20

王智(1985-)，男，甘肃白银人，硕士研究生，研究方向为飞行器动力学与控制；

唐硕(1963-)，男，四川达州人，教授，博士生导师，研究方向为飞行器动力学与控制、飞行仿真等；

闫晓东(1981-)，男，内蒙古呼和浩特人，讲师，博士，研究方向为飞行器动力学与控制。

V412.4

A

1002-0853(2012)02-0175-06

(编辑：王育林)