抑制飞控系统舵机间隙影响的非线性补偿器设计
2012-11-03黄立梅吴成富马松辉
黄立梅, 吴成富, 马松辉
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
抑制飞控系统舵机间隙影响的非线性补偿器设计
黄立梅, 吴成富, 马松辉
(西北工业大学 无人机特种技术国家重点实验室, 陕西 西安 710065)
通过对舵机间隙非线性特性的分析和极限环的定义及产生条件的讨论,在飞控系统中采用非线性补偿的方法,设计了间隙补偿器,并介绍了其工程实现方法,进行了相应的数字仿真和半物理仿真试验以及试验结果的对比分析。结果表明,此方法有效地解决了飞控系统由于舵机间隙引起的超调与极限环振荡现象,使飞控系统对舵机的频率特性以及间隙各方面要求大大降低,其工程实现方法简单实用、普遍性较强,具有较高的工程应用价值。
飞控系统; 非线性; 间隙补偿; 极限环
引言
受设计、生产、加工等多个环节的影响,实际飞控系统的执行机构存在多种非线性环节,如死区、间隙、饱和等,而这些非线性常导致飞控系统产生稳态误差和极限环振荡。而且实际控制系统存在多级信号延时,此时较小的非线性也可能引起极限环振荡,对于自身稳定性较弱的飞行器,此种情况更易产生,因此必须解决非线性问题。目前,大多通过线性补偿以及参数调整的方法来抑制非线性影响[1-2],其效果有限。随着现代控制方法的发展,自适应、变结构、智能控制等也用来抑制非线性影响,但其控制方法相对复杂[3]。邱晓红等[4]针对不确定的非线性提出了仿线性元件的思想以实现期望的稳定裕度,针对确定的非线性,提出了非时变非线性可补的概念并做了简单试验,但并未涉及其工程实现。
本文针对无人机飞控系统中舵机间隙非线性问题,采用非线性补偿的方法设计了相应的非线性补偿器,介绍了其工程实现方法,控制系统的数字仿真及半物理仿真试验结果表明,所设计的非线性补偿器很好地抑制了舵机间隙非线性。
1 舵机间隙模型分析
伺服系统的非线性主要为饱和与间隙,针对间隙非线性,目前主要有迟滞模型、死区模型和“振-冲”模型。对于电传伺服系统,其相位滞后对控制系统影响比较大,所以在此以迟滞模型来描述舵机间隙。
间隙的迟滞模型[5]为:
式中,θ为驱动转轴转角;θp为从动轴转角;2α为间隙大小;m为驱动、从动部分的传动比。
间隙迟滞模型示意图如图1所示。
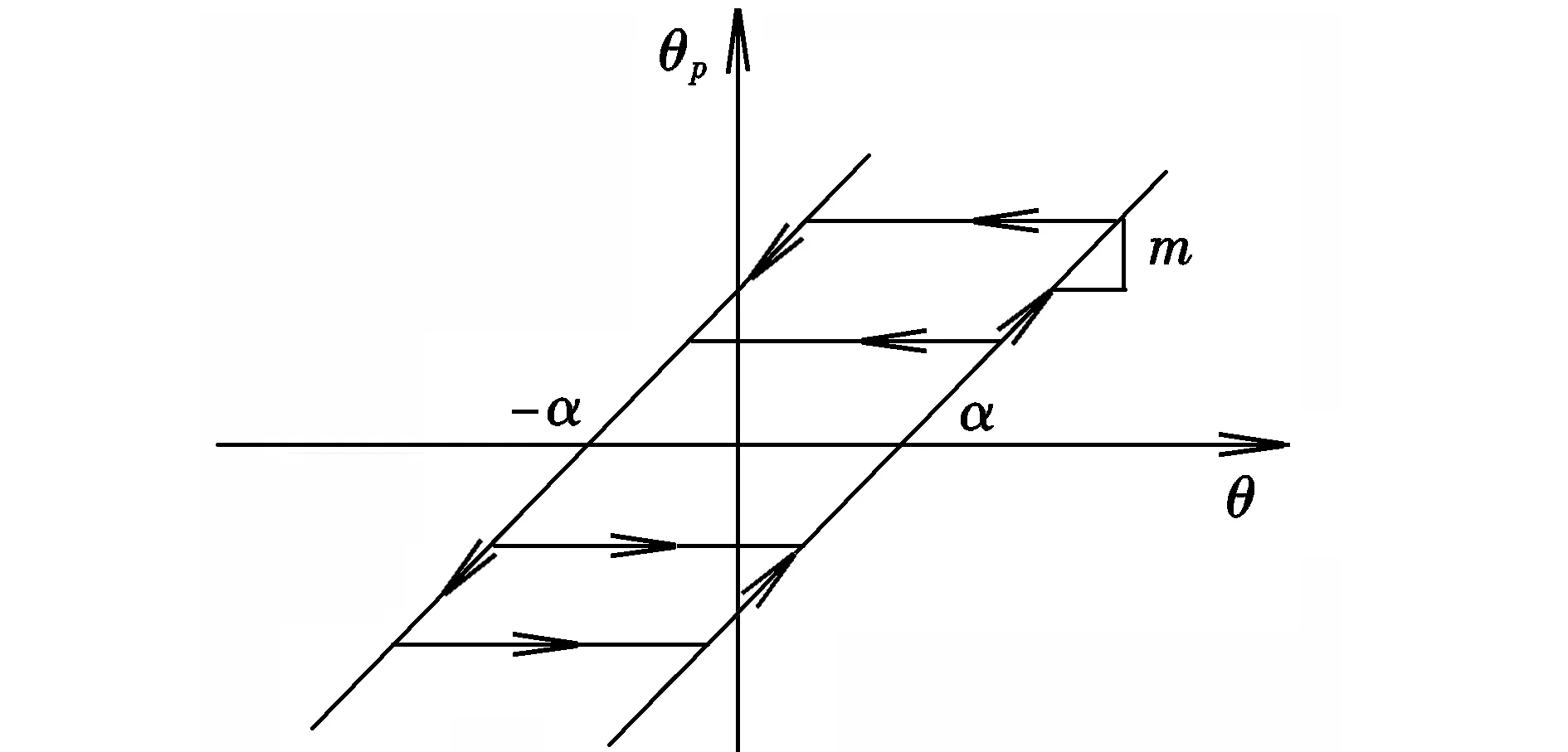
图1 间隙的迟滞模型
舵机间隙对控制系统性能有很多不利影响,主要有:
(1)降低系统稳定性。当舵机间隙达到一定值时,系统产生极限环振荡,此时系统的动态性能与稳定性显著下降,控制效率降低。
(2)使系统产生相位滞后,影响系统快速性。间隙越大,相位滞后越严重,对控制系统相位裕度的要求越高。
(3)降低了舵机系统的定位精度,使控制系统产生一定的稳态误差。
(4)由于间隙存在,机构承载时会有冲击现象,降低了机构可靠性,间隙较大时可能使系统响应超调。
间隙引起的相位滞后可由下式计算[6]:
(1)
式中,α为间隙;A为输入信号幅值。
若间隙为0.2°,输入信号幅值为1°,则产生的相位滞后为11.53°;当输入等于间隙时,相位滞后为90°;在小幅值输入且相位滞后达到180°时,系统就会产生极限环振荡[7]。
2 极限环理论及产生条件
对于平面自治系统[8]:
(2)
有闭轨迹Γ,若存在δ>0使系统在Γ的两侧邻域S(Γ,δ)内的一切轨迹均以Γ为其Ω或A极限集,则称Γ为系统的一个极限环,即在某连通区域内存在孤立闭轨迹的系统存在极限环。下面介绍其判定定理。
从控制理论分析,是系统内部非线性环节增加的奇点使系统相轨迹出现了闭轨,从而产生极限环;从物理结构分析,由于非线性特性作用,使系统能从非周期性的能源中获取能量以维持其周期运动。针对舵机间隙,当舵机主动轮转向时,需先越过两倍的间隙,不直接驱动负载,导致能量积累。当主动轮越过间隙重新驱动负载时,积累能量的释放将使负载运动变化剧烈。当间隙过大,储能过多,则会引起系统的极限环振荡。
3 非时变非线性补偿器概念及性质

f(x+g(x))≡Kx
(3)
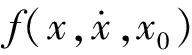
由以上定义可得出补函数的求解方法,即求解方程(3)。
实际系统存在多种非时变非线性,例如饱和、死区、间隙非线性等,对于饱和特性是不可补的,而死区与间隙都可找到其补函数。从补函数定义可看出,只要找到其非线性部分的逆函数,其补函数就很容易求出。
由间隙迟滞模型可得其逆函数[5]为:
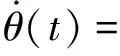
式中,θd(t)为舵机期望输出值;g(τ,t)=2αδ(τ-t)为2α垂直跳跃;δ(t)为Diracδ函数。
从以上逆函数表达式可以看出其类似于微分与理想继电器串联的特性,结合补函数定义,可得出间隙的补函数为微分环节和理想继电器串联组成的环节。
具有非线性补偿的控制系统结构框图如图2所示。

图2 非线性补偿控制系统结构图
针对舵机间隙非线性,前馈非线性补偿通道G(s)为微分和理想继电器串联环节。
4 间隙非线性补偿器设计及实现
4.1 间隙非线性补偿器设计
无人机飞控系统舵机模型主要考虑饱和与迟滞间隙,系统的舵机模型如图3所示,其中饱和范围为±30°,间隙宽度为0.5°,时间常数T=0.1 s。
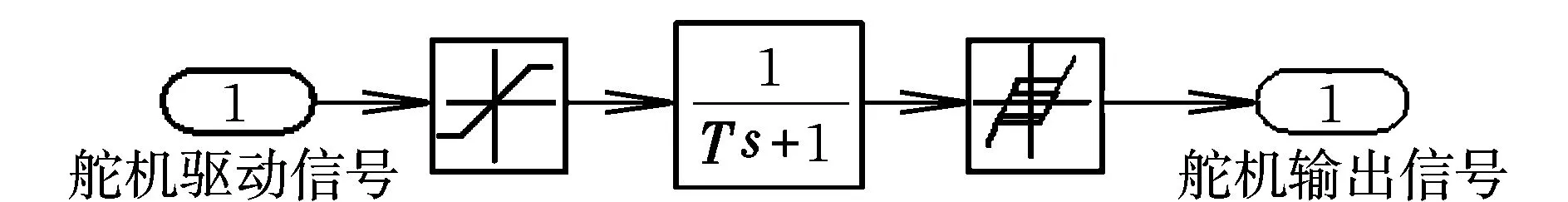
图3 飞控系统的舵机模型
舵机间隙补偿器数字仿真模型如图4所示。
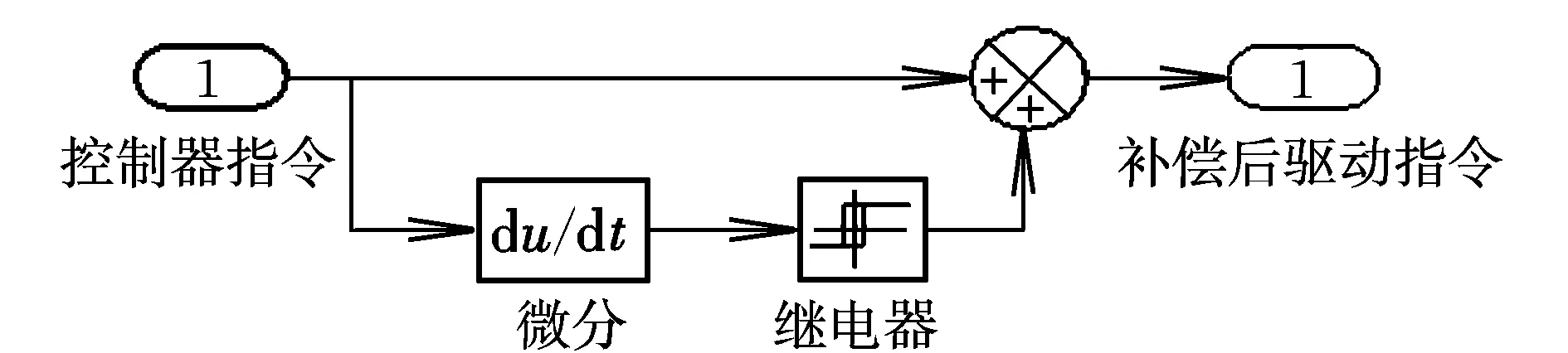
图4 舵机间隙补偿器模型
4.2 间隙补偿器工程实现
本实验采用F28335芯片作为飞控计算机的控制与解算单元。主要试验流程如图5所示。

图5 飞控系统试验流程图
间隙补偿环节的逻辑结构见图2,整个控制流程采用C代码实现。
间隙补偿环节的工程实现关键在于微分和继电器的实现。实际中,实现精确微分比较困难,实现不当会给系统加入噪声,如果噪声较大应考虑加入滤波器。本文采用离散化微分函数K(z-1)/Tsz,即y(k)=[u(k)-u(k-1)]/Ts,继电器实现很容易根据继电器特性写出其C语言函数实现,在此不再赘述。
5 仿真结果分析
分别针对无间隙、有间隙无补偿、有间隙有补偿三种情况进行数字仿真和半物理仿真试验(以俯仰角保持回路为例)。
飞控系统的俯仰角保持回路控制律为:
δe=kθ(θ-θc)+kqq
5.1 数字仿真试验
三种情况下的数字仿真试验结果如图6所示。
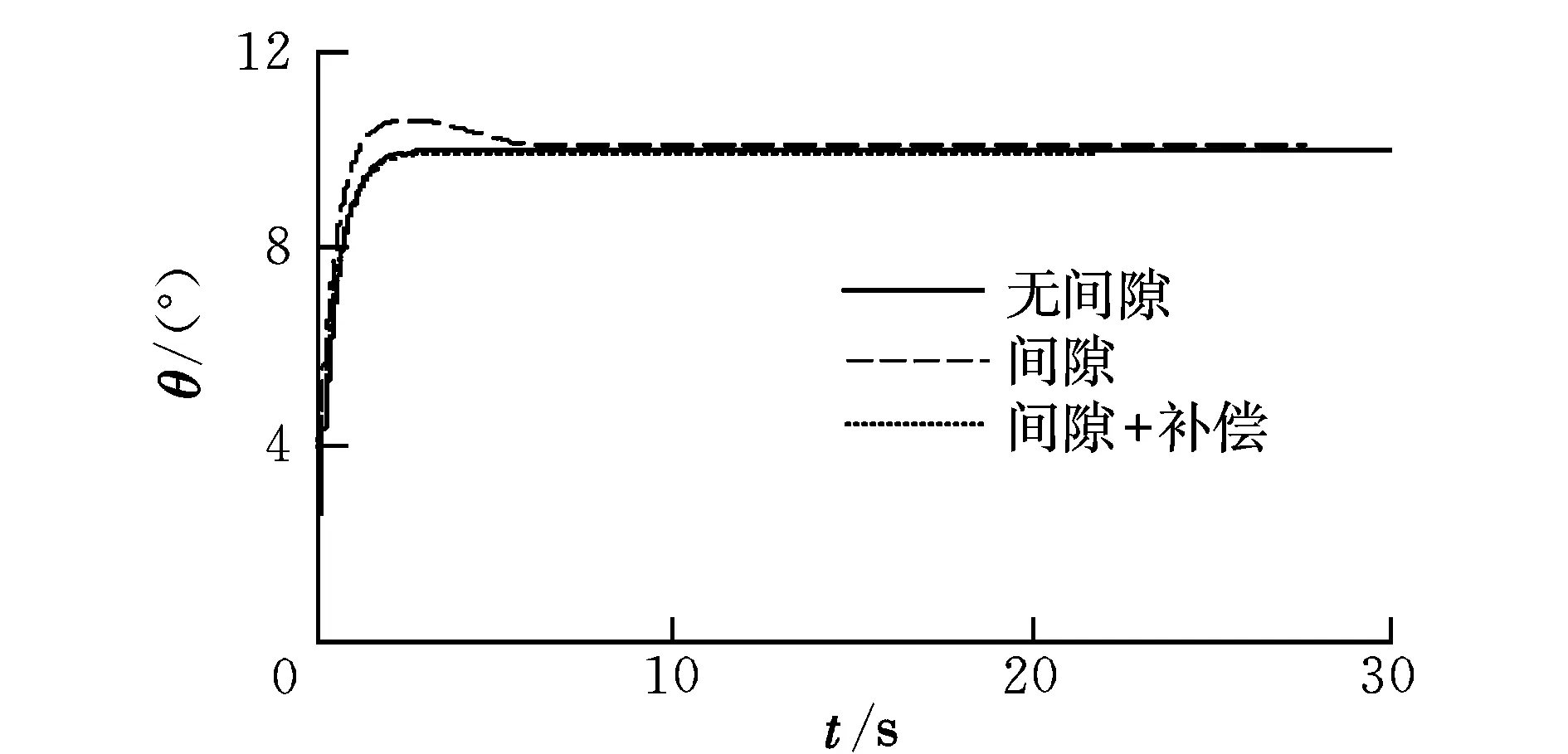
图6 数字仿真试验结果
图6中,舵机间隙使系统产生较大超调和较小稳态误差,但无极限环振荡,此时设计的控制器相位裕度足以抑制舵机间隙引入的相位迟滞。加入间隙补偿后,间隙引起的超调几乎完全被消除,补偿效果很好。
5.2 半物理仿真试验
三种情况下的半物理仿真结果如图7所示。
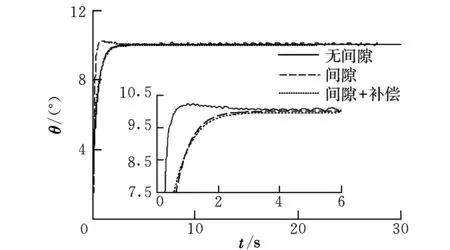
图7 半物理仿真试验结果
图7中,舵机无间隙时响应很平稳,无振荡,加入间隙后,飞控系统产生了小幅值极限环振荡,这说明加入实际系统传感器、舵机驱动等纯延时环节后,间隙带来的相位迟滞对系统稳定性影响较大,随着系统响应进入稳态,舵机输入为小幅值信号时达到极限环产生条件。加入补偿后,间隙的相位滞后、超调以及极限环振荡被消除,系统响应比较理想。
5.3 结果对比分析
综合以上结果,对于有间隙无补偿系统,数字仿真时,间隙非线性只引起系统超调,而半物理仿真时除超调外还引起了极限环振荡,这是由于半物理仿真系统相位迟滞远大于数字仿真系统,此时再加入间隙非线性的相位迟滞,使系统达到了极限环产生的条件。加上间隙补偿后,数字和半物理仿真都很好地抑制了非线性影响,同时通过间隙补偿,也降低了飞控系统对舵机的性能要求。
6 结束语
文中针对舵机间隙非线性设计了非线性补偿器,介绍了其工程实现,并通过数字仿真和半物理仿真试验,表明此方法有效地解决了实际飞控系统由于舵机间隙引起的稳态误差、超调和极限环振荡,其工程实现方法实现简单,具有很好的普遍适用性。
[1] 高金源.线性模型跟踪抑制电传飞行控制系统极限环 振荡实验研究[R].北京:北京航空航天大学,BH- B2363,1986.
[2] 孙国范.排除电传系统极限环振荡的探讨及试验验证 [J].飞行力学,1988,6(1):81-95.
[3] Tao G,Kokotovic P V.Adaptive control of systems with backlash[J].Automatic,1993,29(2):323-335.
[4] 邱晓红,高金源.抑制飞控系统极限环的非线性方法 [J].航空学报,1994,15(7):847-852.
[5] 赵国峰,樊卫华,陈庆伟,等.齿隙非线性研究进展 [J].兵工学报,2006,27(6):1072-1077.
[6] 李朝富.提高电动舵机动态特性的方法研究[J].战术 导弹控制技术,2008, 30(2):37-40.
[7] 朱恩,盛洁,王蔚南, 等.一种抑制电传系统PIO的非 线性补偿方法[J].南京航空航天大学学报,1998,30 (4):400-404.
[8] 高崚嶒.极限环的存在性和稳定性的判断及求解[J]. 宿州教育学院学报,2007,10(2):119-121.
Designofanonlinearcompensatorfordepressingtheinfluenceofactuator’sclearanceinflightcontrolsystem
HUANG Li-mei, WU Cheng-fu, MA Song-hui
(National Key Laboratory of Special Technology on UAV, NWPU, Xi’an 710065, China)
After analyzing the characteristic of clearance of actuators, a new clearance compensator is designed applying the nonlinear control theory. And how to implement it in engineering is discussed. The results of full digital and real-time semi-physical emulation tests show that this nonlinear method is valid to depress the influence of nonlinearities so that the requirements of the performance of actuators is reduced, what’s more, it is simple in use, universal, and of high engineering utility.
flight control system; nonlinearity; clearance compensation; limit-cycle
2011-07-01;
2011-10-20
装备预研基金资助(9140A25030109HK03)
黄立梅(1986-),女,陕西西安人,硕士研究生,研究方向为无人机控制。
V249.1
A
1002-0853(2012)02-0132-03
(编辑:王育林)
