基于隐身的三维航迹规划研究

陈中起, 于雷, 周中良, 鲁艺

(空军工程大学 工程学院, 陕西 西安 710038)

基于隐身的三维航迹规划研究

陈中起, 于雷, 周中良, 鲁艺

(空军工程大学 工程学院, 陕西 西安 710038)

为提高飞行器对地攻击效能,必须对其三维航迹规划技术进行研究。考虑到威胁并非不可穿越,建立了间歇式暴露模型;通过考虑飞行器姿态变化对暴露范围的影响,建立了飞行器战术隐身模型;对传统稀疏A*算法进行了改进,有效提高了规划速度,在此基础上提出了具有实时规划能力的分步规划算法,并给出了解决在线重规划的方法;最后,在真实地形下进行了仿真验证,仿真结果证明了所建模型及算法的有效性和实用性。

运筹学; 间歇式暴露; 飞行器隐身; A*算法

引言

航迹规划技术是任务规划的关键技术,其目的是在规划空间内寻找一条或几条从起点到终点满足各种约束的最优飞行轨迹。传统的航迹规划问题是按照预先选定好的代价函数,通过一系列的算法搜索,找到一条使代价函数值最小的航迹。目前国内外对航迹规划的研究非常多,但普遍存在的问题有:一是将飞行器视为质点[1-2],没有考虑飞行器姿态对航迹的影响;二是为了避开因考虑复杂威胁环境而带来的庞大计算量,多将威胁作简化处理[3],并认为威胁不可穿越[4];三是将规划分为水平和垂直两个二维规划分别进行,因此而带来的规划误差很难避免;四是所选用的规划算法速度慢,仅适用于小范围区域,达不到在线重规划的时间要求[5]。

基于此,首先为控制暴露时间,建立了间歇式暴露模型;其次建立了飞行器战术隐身模型,考虑了飞行器姿态对航迹的影响;第三,对稀疏A*算法(SAS)进行了有效改进,使规划速度得到极大提高,提出了一种具有实时规划能力的分步规划方法,并将其应用于在线重规划中;最后,在真实三维地形中进行了仿真验证。

1 关键模型的建立

1.1 间歇式暴露建模

飞行器突防时并非被发现即被毁伤,由于导引头截获时间(t1)、武器准备时间(t2)和决策人员反应时间(t3)等因素影响,研究飞行器在威胁区暴露时间(t),实现在敌防空武器发射前逃离探测区,破坏武器发射条件,从而躲避攻击,对提高飞行器生存力和任务完成能力具有重要意义,如图1所示。

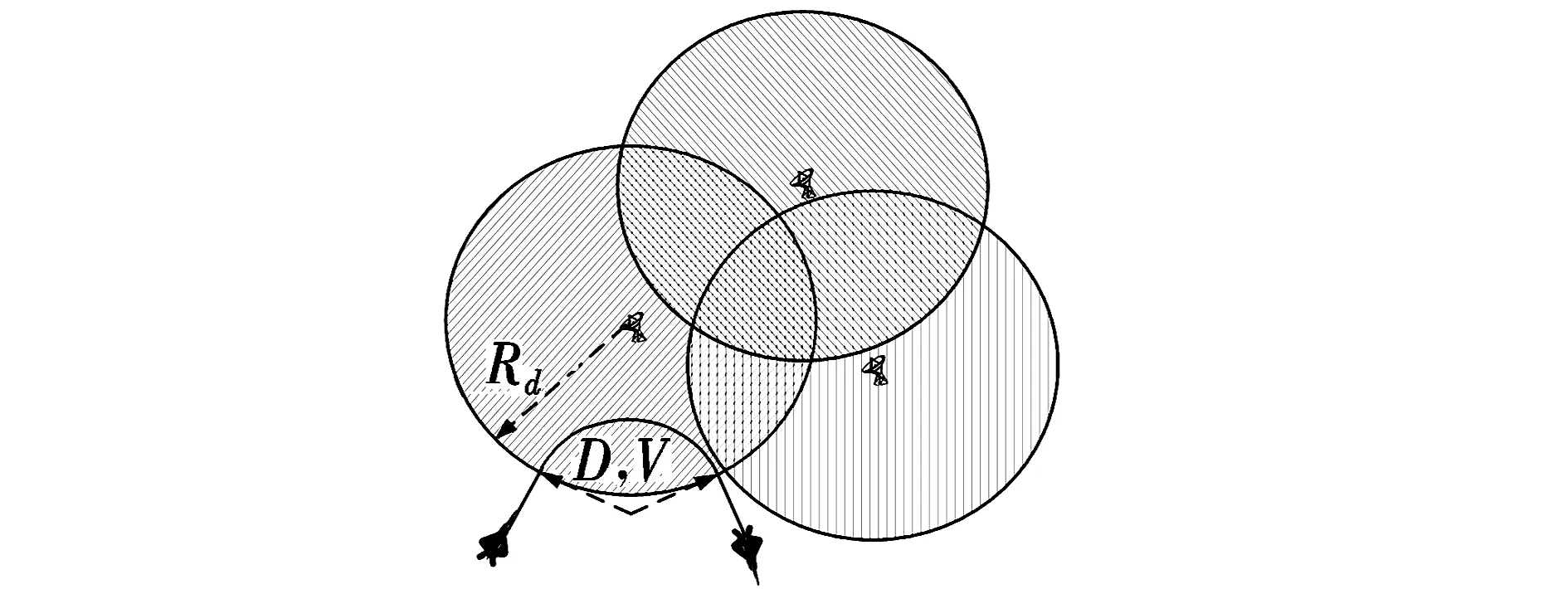
图1 间歇式暴露示意图

于是建立如下模型:

(1)

式中,D为威胁区航迹暴露长度;V为飞行器在威胁区平均速度;tmax为最大允许暴露时间。

1.2 飞行器战术隐身建模

(1)飞行器战术隐身概念

飞行器战术隐身是指利用飞行器RCS的动态变化特性,通过战术机动,不断调整飞行器相对于威胁源的飞行姿态,从而保证其始终处于威胁探测范围之外或满足间歇式暴露条件,进而达到隐身突击的目的。

(2)飞行器RCS简化建模

雷达网对目标的综合发现概率与目标的RCS相关,传统的航迹寻优中,都是将目标视为质点。然而,实际上目标各向RCS不仅不同,而且相差很大,图2为一典型目标RCS周向散射图。由图可知,目标头向和尾向RCS相对较小,两翼部分RCS最大。于是对应的暴露范围也不同,显然,只用一固定RCS值计算雷达网的综合发现概率是有很大局限性的。充分考虑突防过程中,由于飞行器机动带来的暴露范围的动态变化,对提高生存力、提高规划质量具有重要意义。

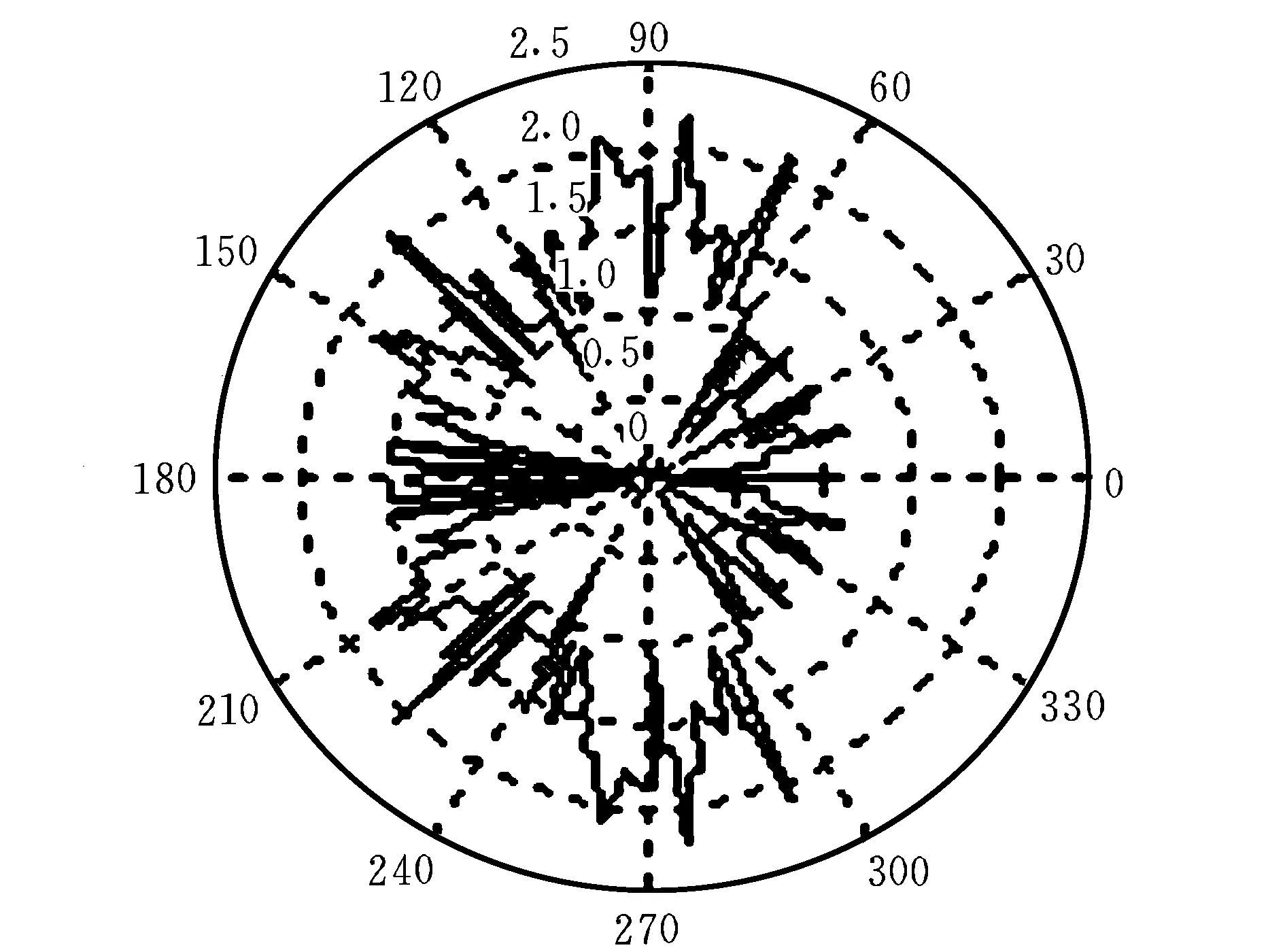
图2 典型目标RCS周向散射图

飞行器各向RCS值很难准确获得,尽管目标周向RCS值变化剧烈,由于飞行器外形原因,其变化是遵循一定规律的。采用文献[6]中的方法将飞行器划分为8个重点区域,分别给出各区域RCS均值进行简化建模,能有效利用飞行器RCS动态变化特性。

(3)飞行器战术隐身的应用

如图3所示,飞行器在突破图中三处威胁时,充分利用其头向和尾向RCS较小的特性,具体战术是:以迎头方向接近威胁(图中B,D,E处所示),以尾部方向退出威胁(图中C,F,H),侧向快速机动(图中BC段、DE段、EF段和FH段)。

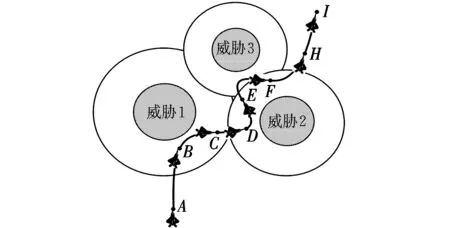
图3 战术隐身示例

2 传统稀疏A*算法的改进

2.1 传统A*算法

在A*算法[7-8]中,保持有两个表:Open表和Close表,分别保存未考察节点和已考察节点。各节点代价值用到的评价函数一般形式为:

f(x)=ag(x)+bh(x)

(2)

式中,g(x)为从初始节点到节点x的实际代价值;h(x)为从节点x到目标节点的代价估计值;a,b为实际代价和估计代价的权重。

2.2 改进稀疏A*算法 (Improved SAS,ISAS)

传统A*算法最大的缺点是信息存储量随着规划空间的加大成指数规律增长,搜索时间长,搜索效率低。2000年,Robert J Szczerba等提出了一种改进的A*算法,称为稀疏A*算法,该算法充分结合了最小直飞距离、最大转弯角、航迹总长约束、最大爬升角/俯冲角、最低飞行高度等限制。而李春华等将其扩展到了三维[9-10]。但他们均是将飞行器视为质点,同时规划速度仍不能有效满足要求,基于此,本文充分考虑了飞行器战术隐身性能,对A*算法做了以下改进。

(1)节点扩展技术

与文献[10]相似,将约束条件结合到搜索空间中去,所不同的是为方便建立节点扩展模型,本文将其限制在一个球形域内,如图4所示。这里给出方位(φ)、俯仰角(θ)处的节点扩展模型,φ是相对于扩展方向左边界的角度,θ是相对于下边界的角度。

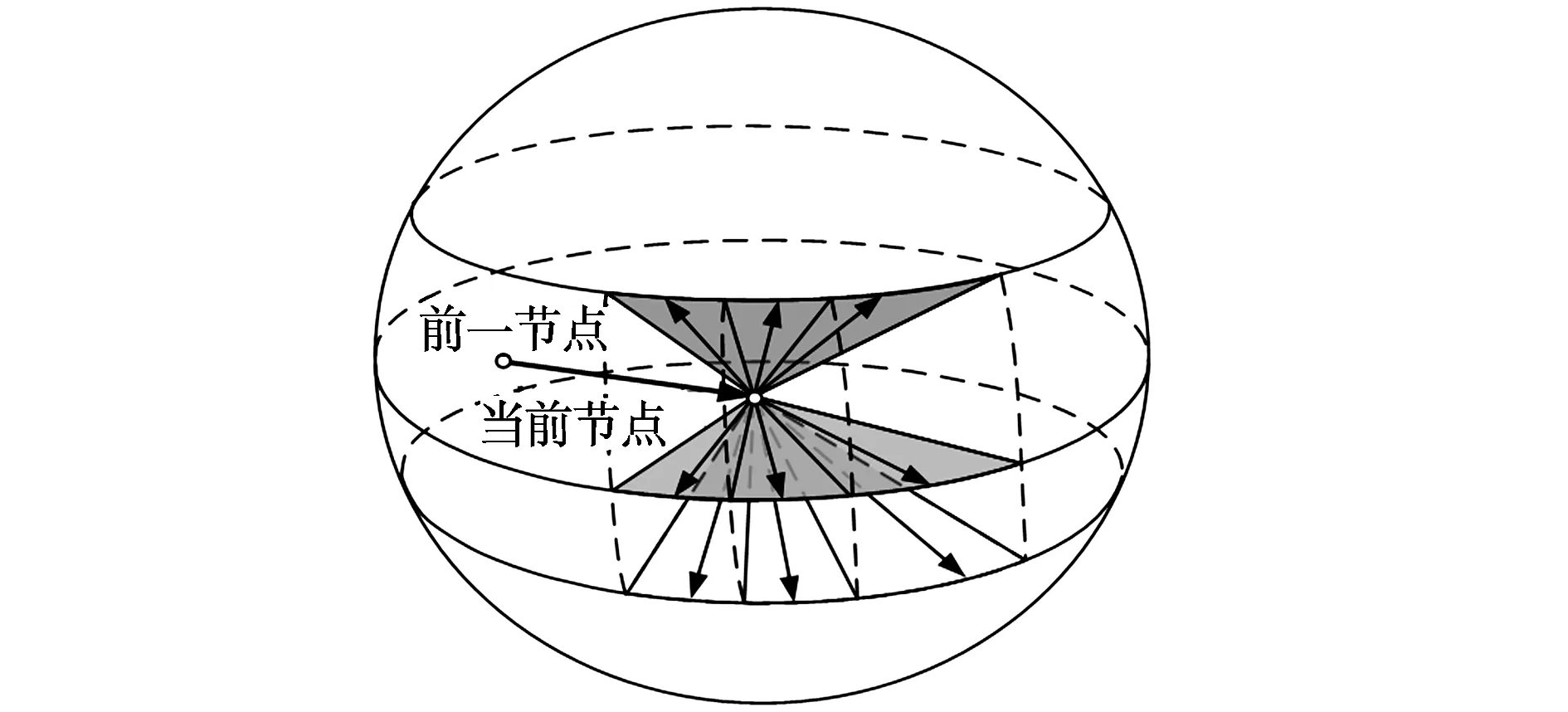
图4 搜索空间示意图

(3)

式中,(xPC,yPC,zPC)为当前节点坐标;Lmin为搜索步长;θmax,φmax分别为最大俯仰角和转弯角;ϑLC为前一节点到当前节点方向相对于地理坐标系x正半轴的夹角。为提高搜索效率,当Open表中的两节点距离小于d时,认为节点重合,从而进一步减少Open表中的节点数,其中d取为:

d=min(Lminφmax/S,Lminθmax/M)/3

(4)

(2)节点控制技术

Open表中的节点数对算法的全局搜索能力和内存占用有很大的影响。传统A*算法对节点数没有限制,虽能保证收敛到最优解,但随着节点数增多,搜索效率将呈指数关系下降,而且Open表中有很多无用节点。因此需要采取有效的节点管理。

Open表管理:为避免对Open表中节点重复排序,从加入第一个节点开始,每次节点扩展都按代价大小插入,最终得到代价值由小到大排列的节点序列。这样既能减少节点排序时间,又方便节点操作。

Open表中节点数控制:结合搜索空间及搜索限制条件,如搜索步长和搜索方向角限制,可确定出Open表中合适节点数Nmax,一般可采用下式:

Nmax=max(X,Y)/Lmin

(5)

式中,X,Y分别为规划空间x方向和y方向的边界范围。当Open表中的节点数超过Nmax时,将扩展的节点插入的同时,去除最后一个节点,从而使表中的节点数始终不会超过Nmax+1。该方法能极大地提高算法收敛效率,但同时存在丢失全局最优解的可能性。

(3)自适应搜索技术

搜索步长对搜索效率也有很大的影响,步长过大会加快搜索速度,但会降低搜索精度,且不易满足限制条件,尤其是目标和威胁附近的进入方向限制;步长过小,会限制搜索速度。因此,根据节点所处位置不同选择合适的步长,采用自适应变步长技术,对提高搜索效率、获取最优解具有重要意义。

(6)

式中, expand(PC)∈T表示当前节点PC扩展的节点处在威胁区域T中;|PCPE|≤2Lmin表示当前节点PC处在目标点PE2倍最小步长范围内。

(4)威胁转化为节点扩展限制技术

传统A*算法的代价函数是威胁代价和航迹代价的加权和。由于是两个不同量纲的量,即使做了归一化处理,各量的变化对总代价值的影响程度仍不同,即总代价值不能反应每个量的变化趋势,使搜索具有一定的盲目性,降低了搜索效率。将航迹规划中的主要威胁——碰地威胁和探测威胁转化到节点扩展限制条件中,使代价函数仅由航迹代价单一量纲组成,同时限制了节点的扩展,提高了规划速度。实现时节点扩展若满足以下任一条件则删除该节点。

(7)

式中,exposure(PCexpand(PC))表示当前节点和新扩展节点间航迹暴露距离;Dmax为最大允许暴露距离;height(PCexpand(PC))表示当前节点和新扩展节点间航迹上任意点高度;Hmin为最低安全高度;Smax为最大航迹长度;D(PC)为到节点PC的实际航迹长度;SL(PC)为节点PC到目标点的直线距离。

(5) 启发式搜索技术

航迹代价函数中的a和b控制着算法的全局搜索和局部搜索能力。a值越大,算法的局部搜索能力越强,即所谓的“深度优先”;b值越大,算法的全局搜索能力越强,即所谓的“广度优先”。一个优秀的启发算法应在初始阶段侧重于全局搜索,而在末段侧重于局部搜索,因此,a和b取值如下:

(8)

式中,PS为起始节点,其余参数同上。

2.3 改进稀疏A*算法基本步骤

(1)计算初始节点P0的f,g和h值,并放入Open表中,此时P0为Open表中唯一节点。

(2)如果Open表为空,算法以失败结束,需重新调整参数,如M,S,Lmin和Nmax的值,重新计算。

(3)从Open表中取出第一个节点Pt,放入Close表中,并作为当前节点。如果满足|PtPE|≤d,则规划结束。由目标点开始向上回溯,直到起始位置。

(4)扩展当前节点:

①判断当前节点是否满足式(6)中的条件,确定步长L;

②构造并分割当前节点的扩展区。如图4所示,将垂直剖面分割成M个扇面,每一扇面分成S个扇区;

③对M×S个小扇区中的每一个,以角度增量δ=0.03判断边界上每一点是否满足式(7)中的任一条件,若满足则跳过该点,计算下一角度增量对应的点,否则计算出该点的代价值f,通过循环计算比较,得到该小扇区代价值最小的点;

④在③中产生的点加入Open表之前要逐一完成如下工作:确定该点与Open表中的节点是否重合。若重合,则比较两点代价值,若该点代价值小于Open表中节点代价值,则首先删除Open表中对应节点,再将该点按代价大小插入Open表;若不重合,则以新扩展节点按代价大小加入Open表。

(5)返回第(3)步。

3 具有实时规划能力的分步规划算法

3.1 分步规划算法

(1)分步规划算法基本思想

前述ISAS算法已使规划速度得到很大提高,但当威胁非常复杂且规划空间较大时,算法的规划速度将受到限制,难以解决此时的实时规划问题。为此,提出了分步规划(Step by Step Plan,SBSP)算法。即,首先规划航迹长度dP,设定实际执行航迹长度dE(dE≤dP),在执行过程中进行下一步规划,飞至执行航迹段结束时直接转入已生成的下一段航迹,从而实现实时规划的目的。

(2)规划效率和执行效率概念

为描述算法可行性条件,首先给出规划效率和执行效率概念。

规划效率(PV):指算法单位时间内所能规划的航迹长度,单位为m/s。它是算法的一个属性,受战场环境影响较大,战场环境越复杂,其效率越低。

执行效率(EV):指飞行器单位时间内所执行的航迹长度,单位为m/s。它是飞行器的一个属性,与飞行速度相等。

显然,实时规划的必要条件如下:

EV≤PV

(9)

(3)SBSP算法基本步骤

①设定dP,dE以及初始条件、航迹约束等信息；

②采用SBSP进行规划,获得第一步航迹。节点扩展后需考察Open表中的每个节点的航迹长度信息。取出所有航迹长度大于等于dP的节点,并从中取出代价最小的节点存入Close表,停止本步规划;若不存在这样的节点,则继续搜索；

③飞行器开始执行由dE及步骤② 确定的下一步规划起点位置及初始航向,并开始进行下一步规划,过程同步骤②,获得下一步航迹。规划时若达到目标点，则整个规划完成;

④执行至本步结束位置时,转入下一步已规划好的执行航迹,返回步骤③。

3.2 针对突发威胁SBSP算法的应用

(1)问题描述

飞行器在沿已规划航迹飞行过程中,如图5所示,在A点探测到前方Rd处原航迹上出现一突发威胁,且探测得知威胁作用半径为Rt。为避开威胁,需综合原有威胁和该新威胁,对原航迹进行在线局部重规划。采用SBSP算法,可得虚线圆弧所示的新航迹,由B点开始沿新航迹飞行,至C点绕开突发威胁后重新回到原航迹上。

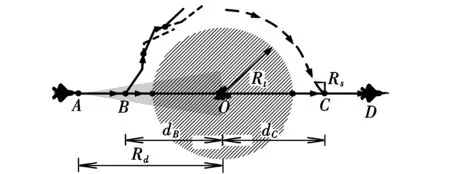
图5 突发威胁处理示意图

(2)新航迹起点B和结束点C的确定

B,C点均在原航迹上,可由下式确定:

dB=dC=Rt+max(Rs,L)

(10)

式中,Rs为飞行器最小转弯半径,其余参数同上。

4 仿真分析

为验证所建模型的正确性及算法的有效性。假设战场范围为(EX1,NY1)～(EX2,NY2),其中E和N分别表示经度和纬度,下同。采用精度为100 m×100 m的数字高程图,利用数字地图处理技术,可得如图6所示效果。为便于计算,假设敌雷达网中各雷达性能参数相同,架设高度50 m;飞行器最短直飞距离Lmin=6 km,最大转弯角50°,最大爬升俯冲角均为20°,最小安全高度200 m,出发点航向角150°,目标点进入角150°,最大允许暴露距离Dmax=3 km,最大航迹长度为起始点和目标点间直线距离1.2倍,发现突发威胁的探测距离35 km;规划起点坐标(EXS,NYS),终点坐标(EXE,NYE);Open表中最大节点数100;M=5,S=3;dP=10 km,dE=8 km。仿真图中距离单位为m。

仿真1:地面两部已知雷达威胁,位置坐标分别为(ERX1,NRY1)和(ERX2,NRY2),其余参数不变。

图6、图7分别给出了ISAS算法和SBSP算法的对比仿真结果。图中,雷达内外两个探测范围是由于飞行器姿态不同对应不同的RCS,进而对应不同的探测距离,图中给出的是最大和最小探测距离。敌雷达由于受地形遮蔽影响,两部雷达间形成了一定的探测盲区。由图可知,两种算法利用地形遮蔽作用均实现了成功突防,图6(b)中虽有部分航迹处在威胁区内,但由于满足飞行器姿态和间歇式暴露条件,仍是安全航迹。需说明的是,图7(b)仅表示垂直面航迹情况,由于dP,dE不等,图中包含有未被执行部分,所以显示航迹长度并非规划结果航迹长度。且图6(a)的规划时间为36 s,图6(b)单步规划时间小于2 s,于是有PV=5 km/s,即使是飞行器做2倍声速突防,有EV=0.68 km/s,EPV=5 km/s,满足式(9)的必要性条件。

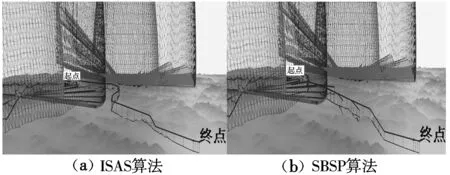
图6 两部雷达时航迹规划图

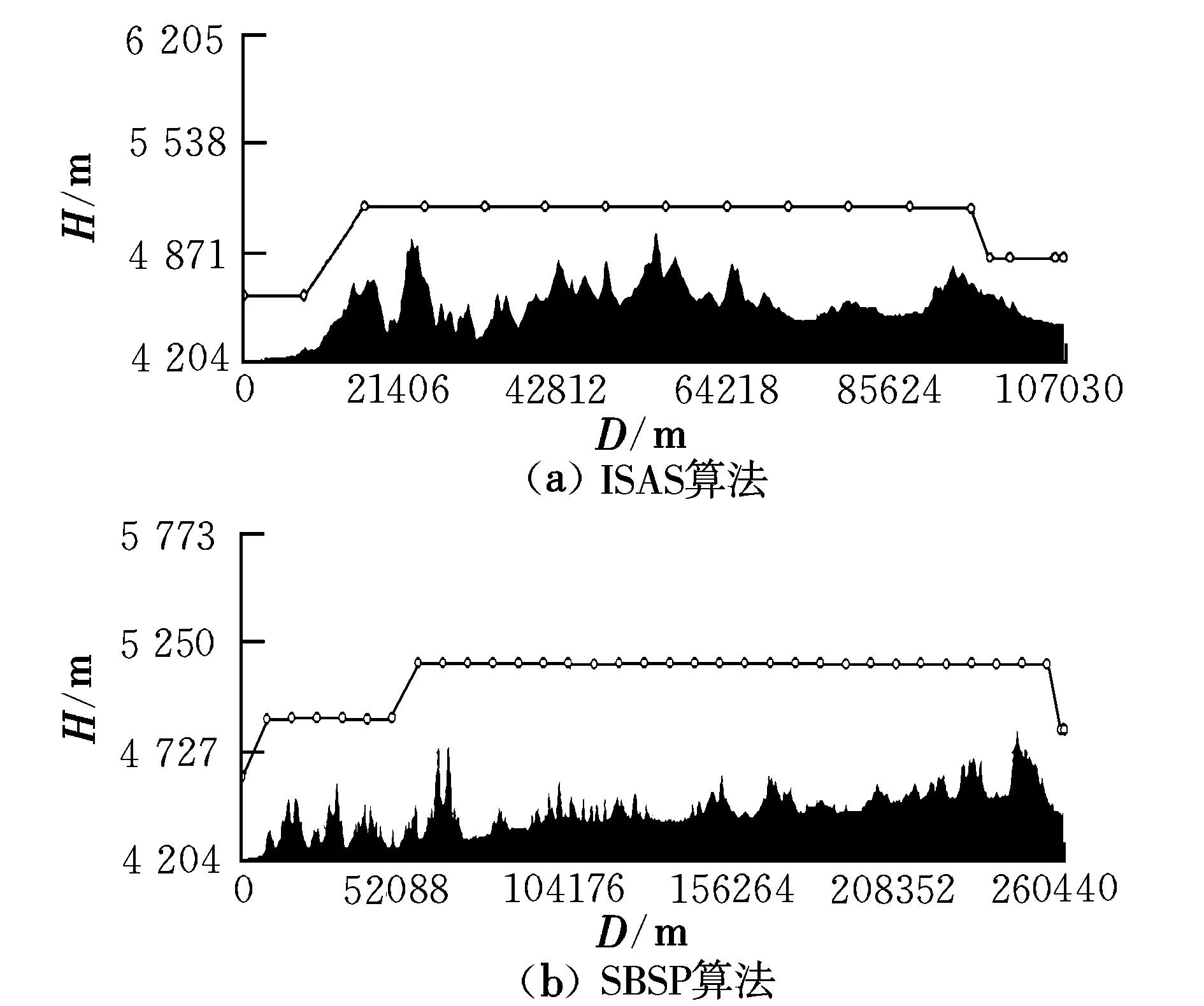
图7 两部雷达时航迹剖面图

仿真2:在仿真1基础上增加突发威胁,位置坐标为(ERX3,NRY3),起补盲作用,飞行器探测到该威胁时进行在线重规划,所得结果如图8、图9所示。

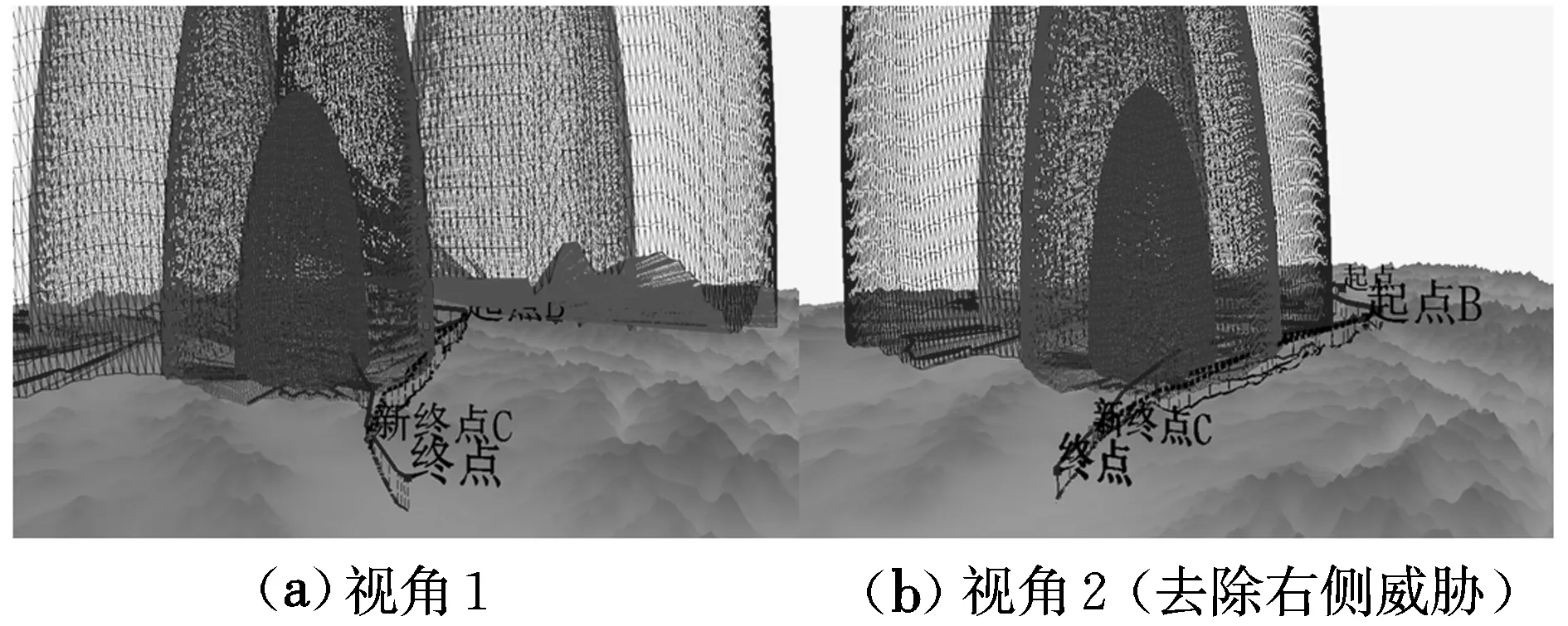
图8 出现突发威胁时航迹规划图

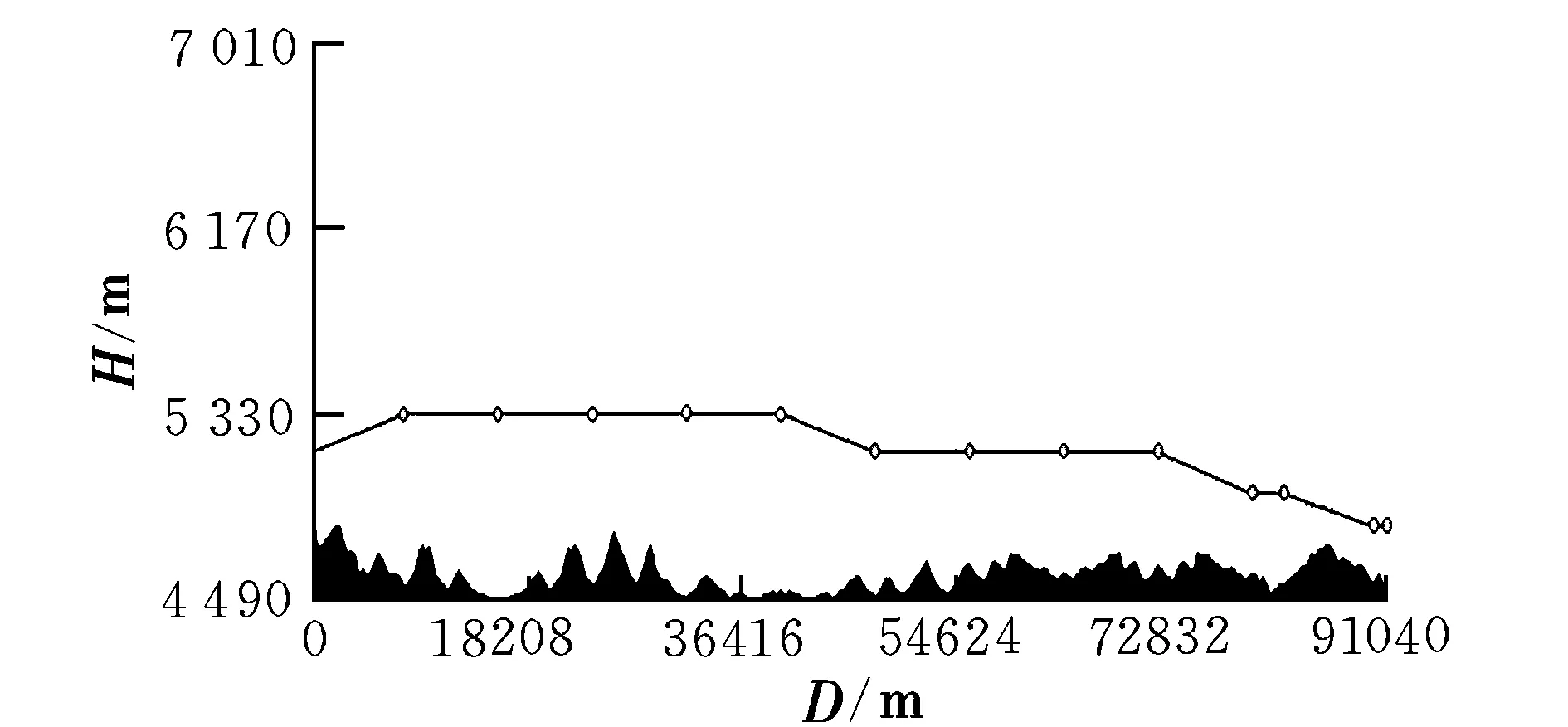
图9 出现突发威胁时在线重规划航迹剖面图

经仿真可知,SBSP算法单步规划的时间仍不超过2 s,满足式(9)条件。图8中，中间威胁即为补盲雷达产生的突发威胁,正好位于原航迹上,飞行器需要进行在线重规划,右侧虚线即为在线重规划所得最优航迹。为便于观察,图8(b)给出了去除最右侧雷达并改变视角后的情况。由图8,结合式(10),飞行器在探测到威胁后,在距突发威胁15 km处“新起点B”开始沿新航迹飞行,在绕过威胁后距其15 km处“新终点C”重新回到原航迹上。由图8(b)可知,飞行器充分利用了战术隐身特性,即使处在威胁区,但通过控制其暴露距离及RCS动态变化特性,实现了安全突防。

5 结论

本文对三维航迹规划技术做了深入细致的研究,所得结论如下:

(1)建立了间歇式暴露模型,为航迹规划安全穿越威胁提供了标准,打破威胁不可穿越的传统;在此基础上,建立了飞行器战术隐身模型,将飞行器动态RCS变化作为一个重要影响因素加入航迹规划中,使规划结果更贴近实用。

(2)对稀疏A*算法作了有效改进,并在此基础上提出了具有实时规划能力的SBSP算法。通过Visual C++和OpenGL进行了仿真验证,结果表明所提SBSP算法具有很好的在线规划能力,能较好地解决飞行器在线局部重规划问题。

[1] 李季,孙秀霞.基于改进A-Star算法的无人机航迹规划算法研究[J].兵工学报,2008,29(7):788-792.

[2] Wang Z J,Fan C,Zhu Q M, et al.3D-Route planning method to realize missile cruise flight[J].Journal of Beijing Institute of Technology,2007,16(2):163-167.

[3] Dai R,John E.Path planning and state estimation for unmanned aerial vehicles in hostile environments[J].Journal of Guidance,Control,and Dynamics,2010,33(2):595-601.

[4] Robert J S.Robust algorithm for real-time route planning[J].IEEE Transactions on Aerospace and Electronic Systems,2000,36(3):869-878.

[5] Rathbun D,Kragelund S,Pongpunwattana A,et al.An evolution based path planning algorithm for autonomous motion of an UAV through uncertain environments[J].IEEE Transactions on Aerospace and Electronic Systems,2002, 38(2):1-12.

[6] 李莹,黄沛霖,武哲.基于不同角域RCS均值的雷达探测模型[J].北京航空航天大学学报,2008,34(6):627-629.

[7] 吴剑,喻玉华,周继强,等.无人机航路规划中的变步长A*算法[J].电光与控制,2011,18(5):1-6.

[8] 郝震,张健,朱凡,等.雷达威胁环境下的无人机三维航迹规划[J].飞行力学,2010,28(1):47-52.

[9] Frank W M.Radar cross-section reduction via route planning and intelligent control[J].IEEE Transactions on Control Systems Technology,2002,10(5):696-700.

[10] 李春华,郑昌文,周成平,等. 一种航迹快速搜索方法[J].宇航学报,2002,23(3):13-17.

Researchon3D-routeplanningbasedonaircraftstealth

CHEN Zhong-qi, YU Lei, ZHOU Zhong-liang, LU Yi

(Engineering Institute, Air Force Engineering University, Xi’an 710038, China)

In order to improve the attacking efficiency of aircraft, 3D-route planning technology must be studied. Firstly, given the problem that threat area can never be passed through being not true, discontinuously exposing model is built. Secondly, by analyzing the effect of aircraft pose changing on the exposing range, the aircraft stealth model is built. Thirdly, quickly planning is realized by improving traditional sparse A-star algorithm, based on which, the step by step plan algorithm is put forward, and at the same time, the re-route planning on-line method is given. At last, simulation is given in real terrain, whose results show that the model and algorithm work perfectly.

operation research; discontinuously exposing; aircraft stealth; A*algorithm

2011-08-22;

2011-12-02

航空科学基金资助(20095196012)

陈中起(1984-),男,河南长葛人,博士研究生,研究方向为航空武器系统总体、仿真与控制。

TP391.9

A

1002-0853(2012)02-0155-05

(编辑：王育林)