循环冗余校验的编码方法比较及文化价值简析

2012-11-01徐金宏

扬州职业大学学报 2012年3期

张铭，徐金宏

(扬州职业大学，江苏扬州 225009)

在计算机的信息传输过程中，为了保证信息的正确可靠，人们采用了特定的编码和校验方法。当信息串行传输时，循环冗余校验(以下简称CRC校验)不啻是一种行之有效的方法。本文研究了采用CRC校验时的除法编码和乘法编码方法，在比较了它们之间的相同和不同之后，特别地揭示了它们之间的内在联系。然后从人文科学的角度简述了CRC校验的广义文化价值。

1 编码方法简述

CRC校验的基本理念:按照一定的规则在k位数据码后缀入r位冗余码，从而构成k+r位的CRC校验码，借以校验通信过程中是否发生差错。这里的r位冗余码之码值取决于生成多项式G(x)。CRC校验的具体编码过程又有除法编码与乘法编码之别。

1.1 除法编码

在CRC校验中，发送端的编码大多采用除法编码。其编码方法如下:

(1)将待编码的k位数据信息位表达为多项式M(x)形式:

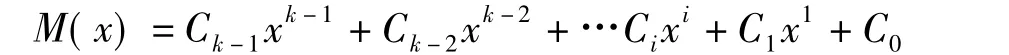
式中Ci的值为0或1。

(2)将信息位组左移r位，即表示为多项式M(x)×xr，这时右边将空出r位，以便放置r位冗余校验位。

(3)选择一个(r+1)次的生成多项式G(x)，对M(x)×xr作模2的除法运算，所得的余数R(x)就是冗余校验位的值。

(4)将M(x)×xr与余数R(x)作模2的加法运算，即可构成(k+r)位的CRC码。从总体效果上看，它相当于在原来的信息多项式M(x)后面拼接了r位冗余校验位。

其编码方法可表示为:

式中P(x)是商式，R(x)是余数。最后:

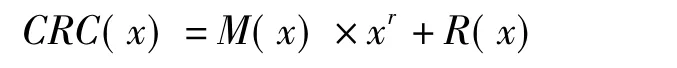
1.2 乘法编码

信息的校验编码过程，实际上是将数据信息根据一定的规则进行某种运算的过程。根据CRC编码和校验原则——余数原则，还可以采用乘法编码。其编码方法是:将信息多项式M(x)和生成多项式G(x)做模2的乘法运算，所得结果就是CRC校验码。其编码方法可以表示为:

显然，这种方法更加直观、简洁、明快。在接收端的校验过程与除法编码校验一样，即用生成多项式G(x)做模2的除法运算。如果在传输过程中没有发生错误的话，显然是能够整除的。

1.3 CRC校验的原则

CRC校验的目标是查错与纠错。在查错方面:当在数据传输无误时，接收端接收到的CRC校验码能够被生成多项式整除(模2除)。我们还发现一个有趣的现象:CRC校验码取反码以后，也是能够被生成多项式整除。这个发现很重要，它是进行除法编码与乘法编码比较研究的重要依据之一。当数据位有任意一位出错时，则CRC校验码不能被生成多项式模2整除，且当数据位循环移位时，其余数也随之发生循环变化，这时可以用余数的变化去“跟踪”出错的数据位。这是查错的基本思想。至于纠错方面，则比较简单，只要将错误位取反码即可。

2 编码方法的比较研究

2.1 编码比较

为了比较除法编码与乘法编码结果的异同，同时为了避免复杂的运算掩盖本文的核心内容，试取4位数据信息的全部16个码字，生成多项式G(x)也只取最简单的形式(1011)，由此得到的CRC(7，4)码见表 1。

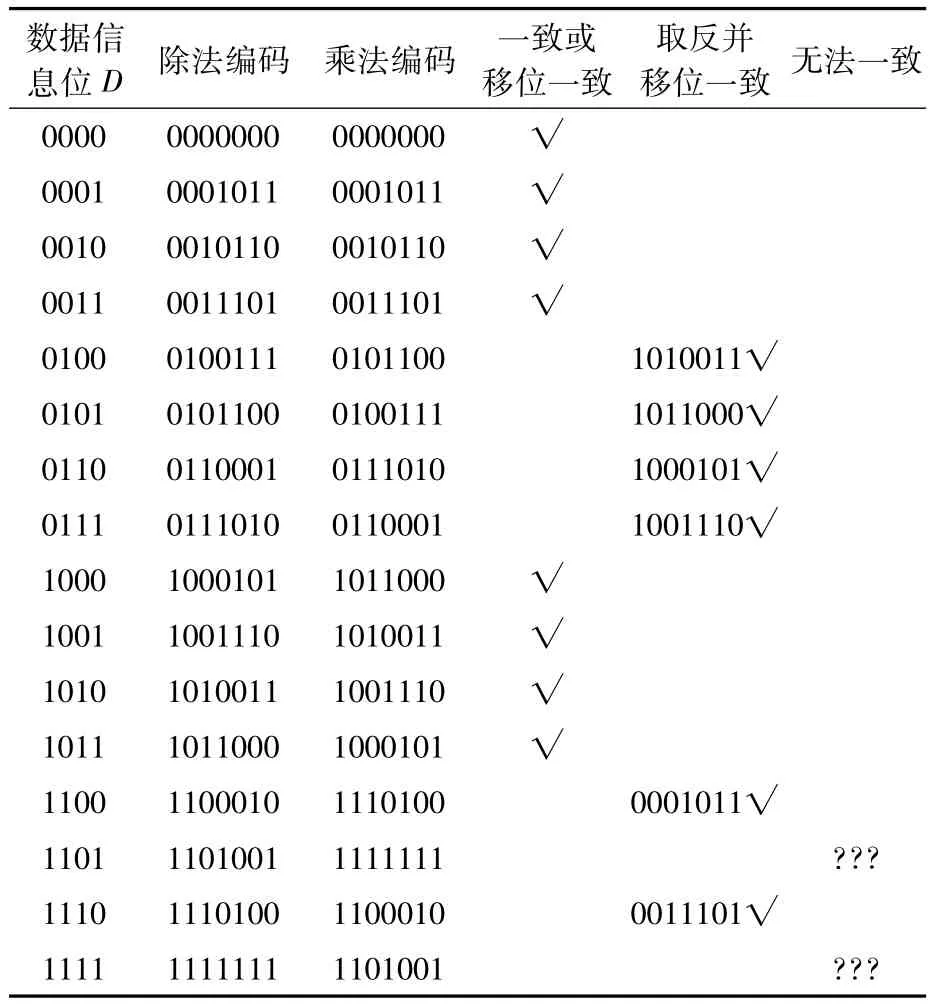
表1 CRC(7，4)码的除法编码与乘法编码结果(G(x)=1011)

显然，两种方法的编码结果总体来说是不同的，这种不同只是表面的。综合CRC编码的特征，可知它们之间有着本质的关联和一致。只要通过适当的变化，充分利用其“循环”的特点，就可以揭示它们的内在的一致性。

表1中的第4列所谓“取反”是指将乘法编码的结果取反。乘法和除法编码的一致性大体有两种情形:一是直接一致或循环移位一致;二是取反码并循环移位一致。循环移位的比较依据是CRC码的本质特征之一(这一操作的意义见下文)，取反码的比较依据是基于模运算。

2.2 对照样本

需要特别注意的是，表1中的第6列(以???标出)，有两组数据，即1101和1111，用上述比较方法无法取得一致。是比较方法有问题还是编码过程中固有的现象呢?为了更好地说明问题，不妨再用其它的生成多项式(比如G(x)=1101)编码，并借以比较之。结果见表2。

在表2中第6列中，同样出现了表1中类似的现象(以???标出)。

表2 CRC(7，4)码的除法编码与乘法编码结果(G(x)=1101)

综合表1和表2的结果表明，对于某一生成多项式而言，各有一对编码无法取得一致。原因为在表1中，生成多项式(1011)与数据多项式(1101)的乘积是(1111111)。这是对应数据多项式与生成多项式一致时出现的“共轭”奇异映射。在表2中，生成多项式(1101)与数据多项式(1011)也出现了类似的情况。

同样的情况也出现在CRC(7，3)码中，生成多项式(11101)和(10111)也是一对“共轭”的多项式。它们对于特定数据组的编码也会出现奇异映射(11000011)。由于生成多项式自身具有一定的特殊性，对于上述现象到目前为止只发现两对。

从本质上来说，除法编码与乘法编码是相通的。当然，这种相通并不是在“四则运算”意义上的相通，而是在“模”运算意义上的相通。

在实际通信过程中，人们普遍采用了除法编码。这是因为除法编码的CRC码数据位和冗余校验位相对集中，并出现在不同的字段上，它易于区分和提取，它的解码时间比较短。但是，从编码过程来看，对于同样的数据位而言，除法编码所需要的操作明显多于乘法编码，这就是说，除法编码是以牺牲发送端的信道编码时间来换取接收端的信息解码时间的。

2.3 比较结论

比较表1与表2，可得以下结论:

(1)对于相同的生成多项式，相应的CRC校验信息是成对出现的。在表1和表2中第2列除法编码的码点全部出现的第3列乘法编码之中了，它们之间是1→1映射的。这就是说，CRC码集具有自封闭性。

(2)在CRC(7，4)中，有3位冗余位。这3位冗余位出现的几率是相等的。冗余码点是23=8，在4位信息的编码中，共有信息码点24=16，CRC校验是一种线性分组校验。理论上说，冗余码字的分组是均匀的，也就是说，它的出现几率是相等的。从表1和表2中可知它们出现的几率是16/8=2，即每一个冗余码点都出现了2次。显然，编码方法不同，冗余位的出现几率是相同的。

(3)在除法编码与乘法编码中，各自总有且只有一对数据信息，不管是移位还是取反移位，它们都无法取得一致。这是编码方法自身的特点所产生的现象。

3 文化价值分析

“文化”是一个很大的，内涵十分丰富的概念。它具有物质的层面和精神的层面。信息传输的校验(或者更广义地包括计算机文化)，其物质层面的意义不必赘述，而它的精神层面，即人文科学层面的意义，通常人们似乎关注得不多。这里的文化价值分析，主要是从社会人文科学的三个不同层面来审视不同的CRC编码与校验的作用和意义。

3.1 经济价值

CRC码的编码与校验方法是近世代数的多项式理论对现代信息传输理论的一大贡献。既经济又巧妙。

3.1.1 技术实现简易

虽然CRC编码在数学原理上来说是复杂的，但是两种编码方法在技术上都是易于实现的。它既可以用软件方式来实现，也可以用硬件方式来实现。为了追求高速度，人们更加青睐硬件方式。它与并行传输校验的海明码校验方法相比较，显得更具有经济价值。

3.1.2 编码结构巧妙

CRC码的码字结构是巧妙的，特别是除法编码方法，它的冗余校验位是在串行传输过程中经校验电路自然而然形成的，并且数据位和冗余校验位出在不同的字段上，它特别易于解码，从而免去了烦琐的信息判断和识别过程。

3.1.3 校验简洁高效

就CRC(7，4)码而言，它用3位冗余位去跟踪7位信息的传输校验，这显然是简洁高效的。

有比较，才有鉴别。CRC校验的经济高效与海明码校方法不便于比较，因为一个是用于串行传输，另一个是用于并行传输。CRC的经济高效可以和奇偶校验相比较。

一维奇偶校验，加入1位冗余位校验后只能查出1位或奇数个错误，它没有纠错能力;二维奇偶校验(纵横奇偶校验，n位并行，传输m位)，需加入n+m位冗余位，它的经济代价太大。而CRC校验，加入n位冗余位后，可以监视2n－1位，而且能够纠正一位出错的情况。

3.2 审美价值

3.2.1 奇异性审美

在自然科学美学中，审美价值有五大方面:简洁、统一、对称、奇异、思辨。CRC码具有独特的对称审美价值，这个问题往往没有得到足够的关注。在表1中，任取CRC(7，4)码的一个码字，比如1001110，经6次循环左移位后，分别得到其余6 个码字:0011101，0111010，1110100，1101001，1010011，0100111。我们发现，这6个码字都是能够被生成多项式G(x)=1011整除(模2除)的。这是一个有趣的现象。

经6次循环右移位后得到的新码字，也具有这样的特性，CRC(7，4)码的任意一个码字都具有这样的特性，这不能不说CRC码是独具奇异美感的。

3.2.2 对称性审美

CRC码的对称性审美价值，一方面表现在CRC码除法编码和乘法编码的码点分布的对称性，详见前文1.3之结论。另一方面，CRC码左循环移位和右循环移位的对称性。这一奇特的现象或许从另一个侧面再度表明:在宏观自然中宇称是守恒的!

CRC码之所以具有的左右循环对称的特点，这要归功于生成多项式G(x)。生成多项式G(x)可以看作是一种映射函数，通过它的映射，信息码具备了循环整除的特点。这种审美价值是值得关注的。