直觉主义思想概述

刘佳秋

（广东金融学院 思想政治理论课教学部，广东 广州 510521）

直觉主义思想概述

刘佳秋

（广东金融学院 思想政治理论课教学部，广东 广州 510521）

一场关于数学基础问题的大论战，产生了三大数学（哲学）流派，它们分别是逻辑主义学派、形式主义学派和直觉主义学派。直觉主义学派认为任何数学对象都是思维构造的产物，所以一个对象的存在性等价于它的构造的可能性，因此直觉主义者坚持用人类构造性思维活动进行数学研究的方法。并且直觉主义者相信理论的真理性最终取决于理论的实际内容，并且只有通过人类的实践活动才能得到检证。

直觉主义；直觉主义逻辑

19世纪70~80年代，德国数学家康托尔创立了集合论（亦称朴素集合论）。集合论逐渐为大多数数学家所接受，并成为全部经典数学的理论基础。但是，与此同时人们相继发现了一系列集合论悖论，特别是1901年由罗素（B.Russell）发现的罗素悖论，①足以使整座数学大厦倾覆，这是绝对不能允许的。悖论产生的根源何在，能否最终为数学找到一个可靠的逻辑基础，这些问题困扰着数学家和逻辑学家，由此引发了一场关于数学基础问题的大论战，这场论战中产生了三大数学（哲学）流派，它们分别是以弗雷格（G.Frege）、罗素为代表的逻辑主义学派、以希尔伯特（D.Hilbert）为代表的形式主义学派和以荷兰数学家布劳维尔（L.E.J.Brouwer）为代表的直觉主义学派。

直觉主义学派思想源远流长。古代的数学家更多地诉诸直觉，侧重直观的图形分析和计算，而较少用纯逻辑的演绎推理。例如被誉为公理化楷模的欧几里德几何，其基本概念和大部分公理、公设都具有直观的自明性。直觉主义学派的公认的创始人是布劳维尔（Brouwer），他认为任何数学对象都是思维构造的产物，所以一个对象的存在性等价于它的构造的可能性，而自然数是借助于人们的原始直觉创造出来的。因此在数学哲学和逻辑中，直觉主义者坚持用人类构造性思维活动进行数学研究的方法。从事这一理论研究的代表人物主要有海廷（Heyting）、克林（Kleene）、达米特（Dummett）和维尔（Weyl）等。他们认为：“只有在直觉上得到构造的对象（概念）及推理过程才是真正可靠的，而那些在直觉上无法得到构造的东西则是‘形而上学’的假定，即应当从数学中清除出去。”[1]这和古典的方法不同，因为根据古典方法，一个实体的存在可以通过否定它的不存在来证明。对直觉主义者来说，这是不正确的：不存在的否定不表示可能找到存在的构造证明。正因为如此，直觉主义是数学结构主义的一种，但它不是唯一的一类。

一、直觉主义理论：存在必须被构造

直觉主义理论（intuitionism）是第三次数学危机之后为解决数学基础问题而产生的最重要的理论之一，这一理论把数学命题的正确性和它可以被证明等同起来。直觉主义者认为，集合论悖论的出现提醒我们必须依据可信性的要求对整个数学作全面的审查，彻底抛弃那些不符合可信性要求的数学概念和方法。它的一个突出的特点是强调数学中的一切都必须是构造性的，将非构造的对象排除在外，完全不承认非构造性证明，只有给出一个命题的构造性证明，直觉主义者才承认这个命题被证明了。因此强调构造性是直觉主义理论的重要特征，其著名口号是“存在必须等于被构造”，即构造性地建立数学理论，也就是说，所有的数学概念和方法都必须是构造性的，按照可操作的固定的方法都可以在有限之内得到定义和施行。

另外，值得一提的是，直觉主义者从构造性的观点出发，承认排中律p∨劭p在有穷集合上的有效性，而拒绝排中律p∨劭p的普遍有效性。他们认为，排中律是从有限事物中概括出来的，因为对于p和劭p我们总可以在有限之内检验完毕，即任何一个涉及有限事物全体的命题，总是可以通过对这些事物逐一地加以验证，来判明该命题的真伪，因此当对象域有穷的时候，排中律是成立的。但是若将这个规律推广到无穷就是没有根据的，无穷只是处于不停的构造之中，若涉及无穷，排中律就不是有效的。因此他们反对实无穷，而坚持潜无穷②的观点。值得指出的是，直觉主义者并不认为排中律假,只是认为它不普遍有效（涉及无穷的时候不有效）。除直觉主义学派,尚有其它一些不接受排中律的学派，如多值逻辑，特别是三值逻辑，但不接受排中律的原因与直觉主义学派不同。例如在三值逻辑中，使用{T，F，I}作为其真值集,尽管对中间值I的不同解释导致多种三值系统,但都是由于接受命题真值的三值性（多值逻辑为n值性，n为大于等于3的整数），所以它们都不接受排中律。

二、直觉主义逻辑：算子不可互定义

直觉主义学派最初是反对形式化方法的，认为数学活动无需借助于形式语言，形式系统也不能正确地表达数学思想。随着时间的推移,形式化方法在逻辑学研究中被广泛地采用,一些直觉主义学派的代表人物才对形式化方法采取了宽容的态度，发展了自己的逻辑。直觉主义逻辑的公式的语法类似于命题逻辑或一阶逻辑。但是直觉主义逻辑的联结词不像经典逻辑那样是可互定义的，因此他们对逻辑初始联结词的选择是慎重的。在直觉命题逻辑中通常使用→，∨，∧，⊥作为基本连结词，把劭作为劭A=（A→⊥）的简写处理。在直觉主义一阶逻辑中，量词坌，埚都是需要的。下面给出海廷在1930年构造的公理化的直觉主义命题演算系统，[2]它由十条公理和一条推理规则构成（φ，ψ，δ为任意公式，他们是由任意命题变元p，q，r，…和逻辑联结词→，∨，∧，⊥组成的合式的符号序列）：

在经典命题逻辑中，可以仅用两个初始联结词，有可能选取合取、析取或蕴涵中的一个作为原始的，并依据它和否定来定义另两个，甚至可以依据自足算子比如皮尔士箭头“↓”（析非）或Sheffer竖线“｜”（合非）定义它们四个。[3]类似的，在经典一阶逻辑中，一个量词可以依据另一个量词和否定来定义。这是二值原理的推论，它使得这种联结词仅仅是布尔函数。但是，二值原理在直觉主义逻辑中不成立，致使多数经典恒等式只是直觉逻辑中在一个方向上的定理，尽管某些定理在经典逻辑中是两个方向的。它们如下：

合取与析取：

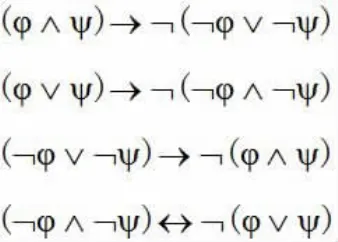
合取与蕴涵：

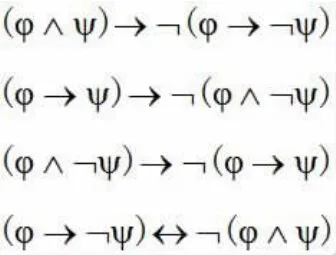
析取与蕴涵：

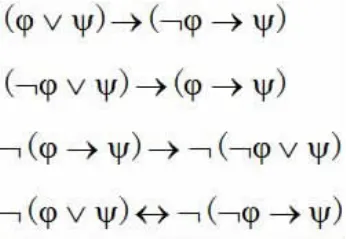
全称量词与存在量词:

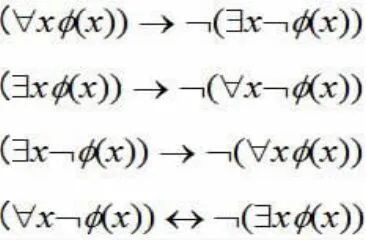
所以，例如，在直觉主义逻辑中，“p或q”是比“如果非p则q”更强的陈述，而在经典逻辑中它们是可互换的。对很多经典有效重言式不是直觉逻辑的定理的观察导致了弱化经典逻辑的证明论的想法。

三、直觉主义逻辑的否定：“劭A”即A不可证实

直觉主义逻辑与经典逻辑的另一个显著区别在于对否定的不同理解。经典逻辑的否定采用的是二值语义：劭p真，当且仅当p假，即如果p真那么劭p假，并且如果p假那么劭p真。直觉主义者根据构造性观点认为，不仅确定一个命题为真需要构造性的证明，确定一个命题为假也需要构造性的证明，因此直觉主义者对否定采取的是构造性解释：一个命题A的否定“劭A”是指存在这样一个有关A的证明，证明A是不可证的。[4]或者说劭A的证明是一个结构，这一结构使得假定命题A为真的构造导致谬误（因为直觉主义者把劭作为劭A=（A→，⊥）的简写处理）。因此，按照直觉主义的观点，说A或B，是宣称A或B可以被证明，也就是要判定一个命题为真，就必须给出它的构造性证明，要判定一个否定命题为真，就必须有一个构造，这一构造将任何一个假定原命题为真的证明转换为一个虚假命题的证明，例如推出一对矛盾的命题B和劭B。正如海廷说：“命题‘C不是有理数’意味着我们能够得到‘C是有理数’的矛盾命题”。[5]因此有些哲学家认为直觉主义逻辑是用肯定词项定义否定范畴的逻辑理论。总之，两种不同的语义解释分别赋予了经典否定和直觉主义否定不同的涵义，如，在经典逻辑中，p的否定的意义是p为假，而直觉主义逻辑中，p的否定的意义是指p不可证或p是可反驳（refutable）的。

在经典逻辑和经典数学中，人们经常不是直接去证明一个命题为真，而是使用反证的间接证明的方法，先假定要证命题不真，然后推出逻辑矛盾，以此来证明此命题为真。显然，反证法这种间接证明是直觉主义者所不能接受的，因为直觉主义者不承认排中律，而反证法用的仍是排中律（A∨劭A），并且从构造性的角度看，假定要证命题不真，推出逻辑矛盾，并不意味着为此命题找到一个构造性证明，即证明了劭A将导致矛盾，这并没有提供A的一个构造性证明。相应地，涉及否定的双重否定律在经典逻辑中是有效式，但在直觉主义逻辑中不再是普遍有效的。因为证明了劭A不可证，并没有实际地给出A的证明，从而劭劭A→A在直觉主义逻辑中不成立，但直觉主义者承认双重否定律的另一方向，即A→劭劭A。可见，很多经典逻辑的重言式在直觉逻辑中不再是可证明的。例子不只包括排中律 p∨劭p，还有反证法，甚至还有双重否定消去规则。在经典逻辑中，p→劭劭p和劭劭p→p二者都是定理，在直觉主义逻辑中，只有前者是定理：双重否定可以介入但不能消去。

逻辑主义认为逻辑是全部数学的基础，经典逻辑是绝对可靠的，只要构造合适的逻辑系统，就可以推出全部经典数学。因此把数学化归为逻辑，是逻辑主义学派的基本纲领，避免悖论，维护集合论和已有的一切数学成果则是其基本出发点。和逻辑主义一样，形式主义学派也坚信经典逻辑的有效性，都持“实无穷”的观点（即承认无限集合是一个完成了的实体），并捍卫一切已有的数学成果。但是形式主义并不赞同逻辑主义“把数学归约为逻辑”的纲领，形式主义学派认为，数学有着与逻辑无关的内容，决不可能单靠逻辑建立起来，应对逻辑和数学同时加以研究。对于形式主义学派方案的反对意见来自直觉主义阵营，直觉主义派则以“直觉上的可构造性”作为“可信性”的标准对全部已有数学进行彻底的审查和改造。直觉主义学派认为，任何一门科学理论都是形式与内容的统一体，理论形式固然重要，形式化方法也有着严格、精密、高度概括与抽象的独特优点，但理论的真理性最终取决于理论的实际内容，并且只有通过人类的实践活动才能得到检证。

（注：本论文得到2008年国家社科基金项目《更新语义与动态认知逻辑研究》的资助，项目批准号：08BZX050）

注 释：

① 集合可以分为两类：第一类集合的特征是：集合本身又是集合中的元素，例如“所有集合所成的集合”；第二类集合的特征是：集合本身不是集合的元素，例如直线上点的集合。显然，一个集合必须是并且只能是这两类集合中的一类。现在假定R是所有第二类集合所成的集合。那么，R是哪一类的集合呢？ 如果R是第一类的，R是自己的元素，但由定义，R只由第二类集合组成，于是R又是第二类集合；如果R是第二类集合，那么，由R的定义，R必须是R的元素，从而R又是第一类集合。这就是著名的“罗素悖论”。

② 所谓“潜无穷”就是把无穷看成一个不断创造着的又永远无法完成的过程,例如把自然数看作一个无限延伸的序列1，2，3…n，…，而不是一个已经完成了的集合N=｛1，2，3…n，…｝。

[1]郑毓信.现代逻辑的发展[M].沈阳：辽宁教育出版社，1989.97.

[2]Heyting，A.“Die formalen Regeln der intuitionistischen Logik I”[J]. Sitzungsberichte der Preussischen Akademie der Wissenschaften，1930.42-56.English translation in Mancosu 1998.311-327.

[3]A.G.Hamilton.Logic For Mathematicians[M].Cambridge University，1978.19-21.

[4]Graham Priest.An Introduction to Non-Classical Logic[M].University of Melbourne，Cambridge University Press，2001.100.

[5]Heyting，A.The Intuitionist Foundations of Mathematzcs[M].reprinted in P.Benacerraf and H.Putnam （eds），Philosophy of illathematzcs，2nd edn，Cambridge University Press，1983.59.